Основные понятия и определения теории

Поиск максимальных потоков в сетях

Магистерская работа по специальности 8.080101

“Математика”

Научный руководитель –

к.ф.-м.н., доцент

Михайлова И.А.

Луганск – 2006 г.

Содержание

Введение………………………………………………………………………….3

Раздел I. Основные понятия и определения теории графов…………………..6

1.1. Понятие графа…………………………………………………….6

1.2. Графическое представление графов…………………………….7

1.3. Виды графов………………………………………………………7

1.4. Элементы графов…………………………………………………8

1.5. Представление графов с помощью матриц……………………..9

1.5.1. Матрицы инцидентности и списки рёбер……………...9

1.5.2. Матрицы смежности…………………………………….12

Раздел II. Потоки в сетях………………………………………………………..14

2.1. Понятие сети………………………………………………………14

2.2. Задача о максимальном потоке…………………………………..16

2.3. Алгоритм размещения пометок для задачи о максимальном потоке………………………………………………………………16

2.4. Алгоритм Форда-Фалкерсона…………………………………18

2.5. Граф со многими источниками и стоками………………………22

2.6. Задача о многополюсном максимальном потоке………………24

Раздел III. Автоматизация поиска максимальных потоков в сетях…………29

3.1. Описание интерфейса программы……………………………….29

3.2. Инструкция пользователя………………………………………30

3.3. Реализация программы…………………………………………33

3.4. Описание программного кода……………………………………38

Выводы…………………………………………………………………………40

Литература……………………………………………………………………….41

Приложение………………………………………………………………………43

ВВЕДЕНИЕ

Начало теории графов все единодушно относят к 1736 г., когда Эйлер не только решил популярную в то время задачу о кенигсбергских мостах, но и нашёл критерий существования в графе специального маршрута (эйлерова цикла, как теперь его называют). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Г.Кирхгофф разработал теорию деревьев для исследования электрических цепей. А математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трёх типов деревьев. К этому же периоду относится появление знаменитой проблемы четырёх красок.

Родившись при решении головоломок и занимательных игр (задачи о шахматном коне, о ферзях, “кругосветное путешествие”, задачи о свадьбах и гаремах и т. п.), теория графов в настоящее время стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей.

За последние десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. В теоретико-графовых терминах формулируется большое число задач, связанных с дискретными объектами. Рассмотрим примеры некоторых практических задач.

1. «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами – дороги (автомобильные, железные и др.) или другие транспортные (например, авиационные) маршруты. Другой пример – сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, а ребрами – возможные маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоков грузов, размещения пунктов производства и потребления и т.д., иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках.

2. «Технологические задачи», в которых вершины отражают производственные элементы (заводы, цеха, станки и т.д.), а дуги – потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.

3. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги – потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами участников цепочки и существующими ограничениями.

4. Управление проектами. С точки зрения теории графов проект – совокупность операций и зависимостей между ними. Хрестоматийным примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).

5. Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства, доверия, симпатии и т.д.) – в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия, и др.

6. Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами – связи (информационные, управляющие, технологические и др.) между ними.

Изучение этих и других подобных им практических задач приводит к теории потоков в сетях. В данной работе рассматривается только одна (но наиболее существенная) задача этой теории, а именно задача нахождения максимального потока.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ

ГРАФОВ

Понятие графа

Пусть V – непустое множество, V ⁽²⁾ – множество всех его двухэлементных подмножеств. Пара (V, E), где Е – произвольное подмножество множества V ⁽²⁾, называется графом (неориентированным графом).

Элементы множества V называются вершинами графа, а элементы множества Е – рёбрами. Множество вершин и рёбер графа G обозначаются символами VG и EG соответственно. Число |VG| вершин графа G называются его порядком и обозначаются через |G|. Если |G| = n, |EG| = m, то G называют (n,m)-графом.

Две вершины u и v графа смежны, если множество {u, v} является ребром, и не смежны в противном случае. Если e = {u, v} – ребро, то вершины u и v называют его концами. Такое ребро обозначают uv.

Два ребра называются смежными, если они имеют общий конец.

Вершина v и ребро e называются инцидентными, если v является концом ребра e (т.е. e = uv), и не инцидентными в противном случае.

Множество всех вершин графа G, смежных с некоторой вершиной v, называется окружением вершины v и обозначается через N(v).

Упорядоченная пара вершин называется ориентированным ребром.

Ориентированный граф (или орграф) – это пара (V, A), где V – множество вершин, А – множество ориентированных рёбер, которые называются дугами, А 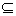V². Если а = (v₁, v₂) – дуга, то вершины v₁ и v₂ называются её началом и концом соответственно. Если граф ориентированный, его обозначают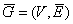

Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же самым множеством вершин, в которых каждое ребро заменено двумя ориентированными рёбрами, которые инцидентны тем самым вершинам и имеют обратные направления. Такое соответствие будем называть каноничным.

Если у ребра начало и конец совпадают, то такое ребро называют петлёй.