Приближенные методы решения задачи коммивояжера
Приближенные методы решения позволяют решать задачу достаточно быстро, но с достаточно большой погрешностью.
Одним из известных приближенных методов является «жадный алгоритм». Суть этого алгоритма в том, чтобы, находясь в определенном городе, выбирать ближайший из ранее не посещенных городов.
Рассмотрим пример кода данного алгоритма на Maple.
> with(combinat):
> N:=9; N1:=N-1;

> PermList:=permute(N1):
> readlib(randomize)();
> random:=rand(1..N*N):
> GTS:=proc(N::posint,start::posint,cost::matrix)
local TourCost, MinCost, MinIndex, index, current;
global Tour;
current:=start;
Tour:= [current]:
TourCost:=0:
while nops(Tour) < N do
MinCost:=infinity:
For index from 1 to N do
if not member(index, Tour) and (cost[current, index] < MinCost)
then MinCost := cost[current, index]:MinIndex:=index
fi
od;
Tour:=[op(Tour), MinIndex]:
TourCost:=TourCost+MinCost:
current:=MinIndex
od;
TourCost:=TourCost+cost[MinIndex,start]
end:
> NearIns:=proc(N::posint, start::posint,cost::matrix)
Local
TourCost, MinCost, MinIndex, index, current, InsPoint, before, after;
global Tour;
MinCost:=infinity:
For index from 1 to N do
if(index<>start) and(cost[index, start] < MinCost)
Then
MinCost:=cost[index,start]:
MinIndex:=index
fi
od:
Tour:=[start, MinIndex, start];
TourCost:=2*MinCost:
while nops(Tour) <= N do
MinCost:=infinity:
For index from 1 to nops(Tour) - 1 do
For current from 1 to N do
if not member(current, Tour) and (cost[current, Tour[index]] < MinCost)
Then
InsPoint:=index:
MinCost:=cost[current, Tour[index]]:
MinIndex:=current
fi
od
od:
after:=cost[Tour[InsPoint+1], MinIndex]-cost[Tour[InsPoint+1],Tour[InsPoint]]:
if InsPoint=1
then InsPoint:=nops(Tour)
fi:
before:=cost[Tour[InsPoint-1], MinIndex] - cost[Tour[InsPoint-1], Tour[InsPoint]]:
if before < after
then InsPoint:=InsPoint-1
Else
if InsPoint=nops(Tour)
then InsPoint :=1
fi
fi:
TourCost:=TourCost+MinCost+min(before, after):
Tour:=[op(1..InsPoint, Tour), MinIndex,op(InsPoint+1..nops(Tour),Tour)]
od:
TourCost
end:
> while true do
> CostMatrix:=matrix(N,N):
> for r from 1 to N do CostMatrix[r,r]:=infinity; od:
For r from 1 to N do
For c from 1 to r - 1 do
CostMatrix[r,c]:=random():
CostMatrix[c,r]:=CostMatrix[r,c]
od
od:
> evalm(CostMatrix);
> MinCost:=infinity:
> for r from 1 to nops(PermList) do
TourPermut:=PermList[r];
TourCost:=CostMatrix[TourPermut[N1],N] + CostMatrix[N, TourPermut[1]]:
For c from 1 to N-2 do
TourCost:=TourCost + CostMatrix[TourPermut[c],TourPermut[c+1]]
od:
if TourCost<=MinCost
then MinCost:=TourCost:
lprint(`Tour->`,[op(TourPermut), N], `Cost=`, MinCost)
fi
od:
> MinGTScost:=infinity:
For r from 1 to N do
GTScost:=GTS(N, r, CostMatrix):
if GTScost<MinGTScost
Then
MinGTScost:=GTScost:
GTStour:=copy(Tour):
print(`Start node->`, r, MinGTScost):
fi
od;
> if MinGTScost>MinCost
Then
lprint(`Minimal GTS cost->`,MinGTScost, `Optimal solution->`, MinCost):
Break
fi;
> od;

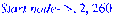
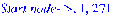
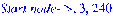
Сложность этого алгоритма O(n^3).Данное решение позволяет вычислять для количества городов порядка 10^3.
Качество решений, получаемых данным алгоритмом, достаточно мало, и в некоторых случаях погрешность вычислений может стремиться к бесконечности.
Еще одним из приближенных методов является метод поиска эйлеровых циклов. Суть этого алгоритма:
v Строится каркас минимального веса(алгоримы Прима или Крускала)
v Каждое ребро дублируется, и каркас превращается в эйлеров граф
v В построеном графе находится эйлеров цикл
v Эйлеров цикл преобразуется в гамильтонов цикл.
Рассмотрим этот алгоритм на Maple.
> with(GraphTheory):
> Letter:=Graph([$1..6],{{1,2},{1,6},{2,6},{2,5},{3,5},
{2,3},{5,6},{5,4},{3,4},{3,6}}):
Так рисуется граф по умолчанию
> DrawGraph(Letter,style=circle);
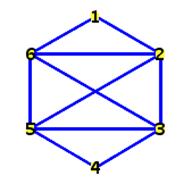
Извлечём в эту переменную последовательность
степеней вершин графа
> eNum:=DegreeSequence(Letter);
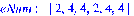
Проверим, что в этом графе существует
эйлеров цикл.
Если получаем пустое множество, то в
графе нет вершин нечётной степени
> remove(type,convert(eNum,set),even);
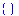
Теперь eNum можно использовать по назначению
> eNum:=NumberOfEdges(Letter);
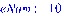
Построение цикла начнём с вершины 1
> start:=5:
Euler:=[]
Будем использовать алгоритм Флёри
> v:=start:
For num to eNum do
Nlist:=Neighbors(Letter,v):
Aset:=convert(ArticulationPoints(Letter),set):
If member(v,Aset)
Then
Aset:=convert(Nlist,set) minus Aset minus {start}:
if Aset={}
then newv:=Nlist[1]
else newv:=Aset[1]
fi
else newv:=Nlist[1]
fi:
Euler:=[op(Euler),[v,newv]]:
DeleteEdge(Letter,{v,newv}):
v:=newv:
od:
> eLetter:=Graph([$1..6],convert(Euler,set)):
> DrawGraph(eLetter);
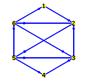
> Euler;
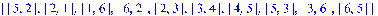
Сложность этого алгоритма O(n*log(n)). Он позволяет вычислять маршрут для количества городов порядка 10^7.
Еще одной эвристикой является Saving Heuristic.
Алгоритм этой эвристики:
v Шаг первый: экономные вычисления
Ø Вычисляем сбережения si j=ci 0 + c0 j - ci j ,для i, j = 1..n, i≠j
Ø Создать nмаршрутов (0,i,0), I = 1..n
Ø Отсортировать полученные сбережения в невозрастающем порядке
v Шаг второй: Наилучшее возможное слияние Начиная с верхней части списка, выполняем следующее:
Ø Учитывая сбережения si j ,определить существуют ли два пути, которые могут быть объединены.
ü Начиная с (0, i)
ü Заканчивая (j, 0)
Ø Объединяя эти два пути, удалив (0, i)и (j, 0),вводим(I,j)
Рассмотрим код этого алгоритма на Maple.
> with(plots):
with(plottools):
> with(combinat):
Number of towns
> N:=8;N1:=N-1:
> PermList:=permute(N1):

> readlib(randomize)();
random:=rand(1..N*N):
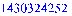
Генерация случайной матрицы
> CostMatrix:=matrix(N,N):
For r from 1 to N do
CostMatrix[r,r]:=infinity
od:
> for r from 2 to N do
For c from 1 to r-1 do
CostMatrix[r,c]:=random():
CostMatrix[c,r]:=CostMatrix[r,c]
od
od;
> evalm(CostMatrix);

Базовый узел
> bn:=1;
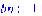
Построение начальных туров
> Tours:=[]:
For r from 1 to N do
if r=bn
Then next
else Tours:=[op(Tours),[bn,r,bn]]
fi
od;
Сама процедура savings
> while nops(Tours)>1 do
MaxSaving:=[[0,0],[0,0],-infinity]:
