Понятие множества. Операции над множествами.

О с н о в н ы е о п р е д е л е н и я. Понятие множества настолько общее, что трудно дать ему какое-либо определение, которое не сводилось бы просто к замене слова “множество” его синонимами: совокупность, собрание элементов и т.п. Не ставя своей задачей сколько-нибудь полное изложение теории множеств, мы здесь лишь введем основные обозначения и приведем первоначальные теоретико-множественные понятия, используемые в дальнейшем.

Множества мы будем обозначать прописными буквами А, В, . . . , а их элементы - малыми x, y, . . . Утверждение “элемент x принадлежит множеству А” символически записывается так: xÎA ; запись xÏA означает, что элемент не принадлежит А. Множество, как совокупность элементов, удовлетворяющих свойству Р, будем записывать в виде

A={ x: x удовлетворяет Р}.

П р и м е р. Пусть Z- множество целых чисел. Тогда, А={ x : x=2k , k ÎZ}- множество четных чисел.

Мы будем говорить , что множество А есть подмножество множества B, и писать АÌВ (или ВÉА), если каждый элемент множества А является элементом множества В.

Если АÌВ и ВÌА, то мы будем писать А=В.

Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Æ. Пустое множество служит подмножеством любого множества.

О п е р а ц и и н а д м н о ж е с т в а м и. Пусть А и В - произвольные множества; их суммой, или объединением С=А È В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А и В.

А

В

Рис. 1

Аналогично определяется сумма любого конечного числа множеств: если А 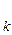(k=1, . . . , n) -произвольные множества, то их сумм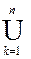а А 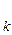есть совокупность элементов, каждый из которых принадлежит хотя бы одному из множеств А .

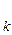Назовем пересечением ( или произведением ) С=А Ç В множеств А и В множество, состоящее из всех элементов, принадлежащих как А, так и В.

А В

Рис. 2

Например, пересечение множества всех четных чисел и множества всех чисел, делящихся на три, будет множество всех чисел, делящихся на шесть. Пересечением любого конечного числа множеств А 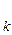называется совокупность 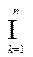А_k элементов, принадлежащих каждому из множеств А .

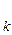Назовем разностью С=А\ В множеств А и В совокупность тех элементов из А, которые не содержатся в В.

Т е о р е м а . Операции сложения и пересечения коммутативны и ассоциативны, т.е.

А È В = В È А, (А È В )È С = АÈ(В È С),

А Ç В = В Ç А, (А Ç В) Ç С = А Ç (В Ç С).

Кроме того, выполняется закон дистрибутивности

А Ç (В È С) = (А Ç В) È (А Ç С).

Д о к а з а т е л ь с т в о. Выполнение первых двух законов очевидно. Докажем дистрибутивность. Допустим, что xÎАÇ(ВÈС). Тогда, xÎА и xÎВÈС, т.е. xÎВ или xÎС (или и то и другое). Значит, xÎАÇВ или xÎАÇС, так что xÎ(АÇВ)È(АÇС). Таким образом,

(А Ç В) È С Ì (А Ç В) È (А Ç С).

Предположим теперь, что xÎ(АÇВ)È(АÇС). Тогда xÎАÇВ или xÎАÇС. Таким образом, xÎА и xÎВÈС. Значит, xÎАÇ(ВÈС), так что

(А Ç В) È (А Ç С) Ì (А Ç В) È С.

Следовательно А Ç (В È С) = (А Ç В) È (А Ç С).