Полярная система координат

Глава 3. Аналитическая геометрия

Общая задача АГ − исследование линий и поверхностей, заданныхуравнениями.

Прямая на плоскости

Общее уравнение прямой.

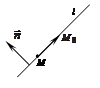В ДПСК на плоскости прямая задается алгебраическим уравнением 1-й степени:

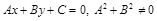. (1)

Покажем, что вектор 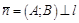. Пусть точки 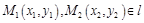. Тогда вектор .

.

.

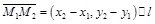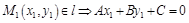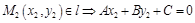Тогда .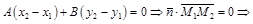

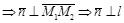Опр.Вектор, перпендикулярный прямой, называется ее нормалью.

Таким образом, если прямая 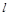задана общим уравнением 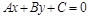, то ее нормаль коллинеарна вектору 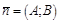, и сам этот вектор можно брать в качестве нормали.

Проведем анализ общего уравнения прямой.

Если С=0, то 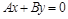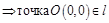, т.е. прямая 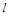проходит через начало координат.

Если В=0, то , , .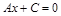

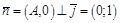
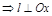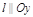Если В=0 и С=0, то 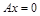, т.е. 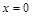- прямая проходит через начало координат , параллельно оси Oy, т.е. совпадает с осью Оу.

Остальные случаи рассмотрите самостоятельно.

2. Уравнение прямой, проходящей через данную
точку перпендикулярно данному вектору

Даны точка 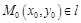и вектор 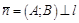. Составим уравнение прямой .

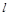Пусть точка 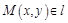. Тогда 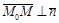. Следовательно, 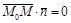. Получаем уравнение прямой :

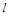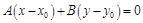. (2)

Пр. Найти уравнение прямой 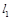, проходящей через точку 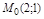параллельно другой прямой .

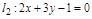Решение. 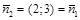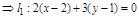или .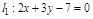

Уравнение прямой с угловым коэффициентом

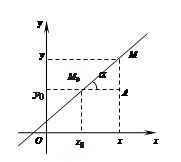Уравнение прямой, имеющее вид

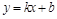, (3)

где 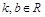, называется уравнением с угловым коэффициентом.

Число 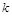называет угловым коэффициентом. Нетрудно установить, что 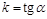, где 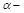угол наклона прямой к положительному направлению оси Оx.

Уравнение прямой, проходящей через данную точку 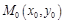с данным угловым коэффициентом k имеет вид:

.

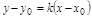Замечание. Уравнением с угловым коэффициентом нельзя задать прямую, перпендикулярную оси Ох. Такая прямая имеет уравнение вида 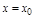(см. п.1).

4. Уравнение прямой, проходящей через данную
точку параллельно данному вектору

Даны точка 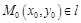и вектор 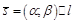. Составим уравнение прямой .

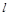Пусть точка 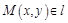. Тогда 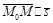. Используя условие коллинеарности векторов, получаем уравнение прямой :

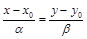. (4)

5. Уравнение прямой, проходящей
через две данные точки.

Пусть точки 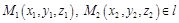. Составим уравнение этой прямой.

Возьмем произвольную точку .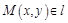

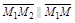
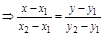. (5)

6. Уравнений прямой в «отрезках».

Пусть точки 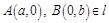. Составим уравнение прямой через две эти точки: 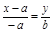. Получаем:

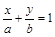. (6)

Совместное исследование уравнений прямых

Пусть даны уравнения двух прямых: 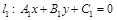и .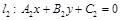

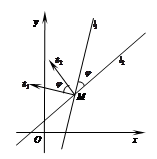а) Точка пересечения прямых: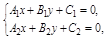

б) Угол между двумя прямым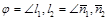и: и 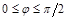. Тогда

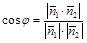или .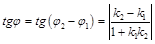

в)Условие параллельности двух прямых:

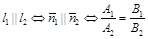или .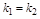

г) Условие перпендикулярности прямых:

.

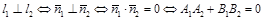Или .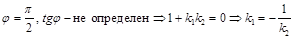

д) Условие совпадения двух прямых: .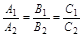

Пр. Проверить, будут ли прямые параллельны, перпендикулярны или найти угол меду прямыми и точку их пересечения, построить прямые: .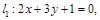

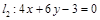Кривые второго порядка.

Опр. Кривой 2–го порядка или линией 2-го порядка называется линия , имеющая в ДПСК уравнение 2-й степени относительно x и y:

, .

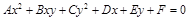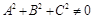1. Эллипс («недостаток» с греч.)

Опр. Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек (фокусов) есть величина постоянная, большая расстояния между фокусами.

Получим уравнение эллипса. Для этого введем на плоскости ДПСК так, чтобы фокусы эллипса 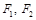были расположены на оси Ох симметрично относительно начала координат (см. рис.). Расстояние между фокусами обозначим 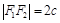. Возьмем произвольную точку 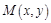, принадлежащую эллипсу. По определению эллипса сумма расстояний от М до 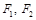есть величина постоянная для всех точек кривой. Обозначим эту сумму 2а, :

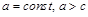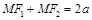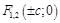. . Следовательно,

;

;

.

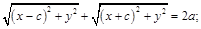
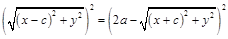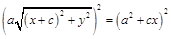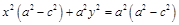Обозначим 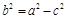. Очевидно, что .

.

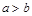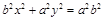Обе части последнего уравнения разделим на .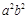

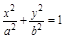. (7)

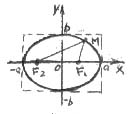Опр. Числа 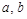называются полуосями эллипса.

Если в уравнении (7) 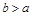, то можно переименовать оси координат. В этом случае фокусы эллипса будут находиться на оси Оу.

Если фокусное расстояние эллипса нулевое, т.е. 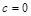, то получаем окружность:

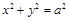(8)

Опр.Оси симметрии эллипса называются осями эллипса, центр его симметрии (точка пересечения осей) − центром эллипса, точки пересечения эллипса с осями − вершинами эллипса.

Опр.Отношение расстояния между фокусами к большой оси называется эксцентриситетом эллипса: 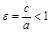(<эллипс>- <недостаток>).

Замечание. 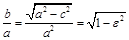. Поэтому:

если 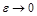, то 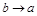и эллипс «круглеет»;

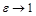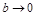если , то и эллипс «сжимается».

Уравнение эллипса в параметрической форме:

,

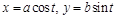где 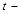угол поворота радиус-вектора точки относительно положительного направления оси Ох.

Параметрическое задание окружности (8):

.

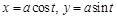Опр. Если эллипс задан уравнением (7) и 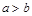, то прямые 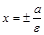называются директрисами эллипса. Если 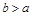, директрисами называются прямые .

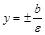Свойство директрисы: для любой точки эллипса отношение ее расстояния 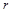до некоторого фокуса к расстоянию 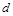до односторонней с этим фокусом директрисы есть величина постоянная, равная эксцентриситету эллипса:

.

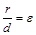2. Гипербола(<избыток, преувеличение> с греч. )

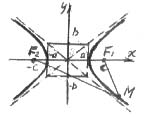Опр. Гиперболой называется геометрическое место точек, модуль разности расстояний которых от двух данных точек (фокусов) есть величина постоянная, меньшая расстояния между фокусами.

Получим уравнение гиперболы. Для этого введем на плоскости ДПСК так, чтобы фокусы гиперболы 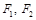были расположены на оси Ох симметрично относительно начала координат (см. рис.). Расстояние между фокусами обозначим 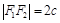. Возьмем произвольную точку 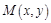, принадлежащую гиперболе. По определению гиперболы модуль разности расстояний от М до 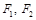есть величина постоянная для всех точек кривой. Обозначим эту величину 2а, 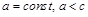: 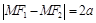. . 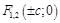Следовательно,

;

;

.

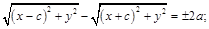
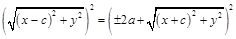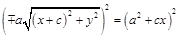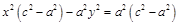Обозначим 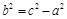. Получим

.

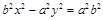Обе части последнего уравнения разделим на .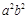

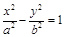. (9)

Опр. Если гипербола задана уравнением (9), то число а называется действительной, а 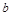мнимой полуосью гиперболы.

Гипербола также может быть задана уравнением

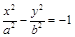. (10)

В этом случае а – мнимая, а 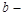действительная полуось.

Опр. Гипербола, у которой 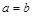, называется равнобочной.

Опр.Прямые 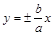называются асимптотами гиперболы.

Опр.Оси симметрии гиперболы называются осями гиперболы, центр его симметрии (точка пересечения осей) − центром гиперболы. Гипербола пересекает одну из своих осей. Точки пересечения гиперболы с осью называются вершинами гиперболы.

Опр.Отношение расстояния между фокусами к длине действительной оси называется эксцентриситетом гиперболы: 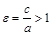(<гипербола>- <избыток>).

Замечание. 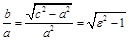. Поэтому:

если 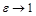, то 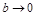и ветви гиперболы сжимаются;

если 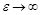, то 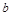становится гораздо больше а, и ветви расширяются.

Опр. Для гиперболы, заданной уравнением (9), прямые 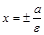называются директрисами. В случае уравнения (10) директрисами называются прямые .

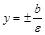Свойство директрисы: для любой точки гиперболы отношение ее расстояния 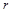до некоторого фокуса к расстоянию 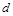до односторонней с этим фокусом директрисы есть величина постоянная, равная эксцентриситету гиперболы:

.

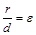3. Парабола (греч.- приложение)

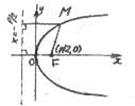Опр. Параболой называется геометрическое место точек, равноудаленных от данной точки F (фокуса) и данной прямой d (директрисы) .

Получим уравнение параболы. Для этого введем на плоскости ДПСК так, чтобы фокус F оказался на оси Ох и имел координаты 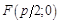, а директриса d совпала с прямой 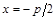, где р – расстояние от фокуса до директрисы. Это расстояние называется параметром параболы. Возьмем произвольную точку 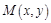, принадлежащую параболе.

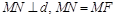. Поэтому

;

;

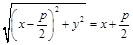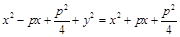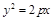. (11)

Если оси Ох и Оу поменять ролями, то парабола будет задаваться уравнением

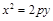. (12)

По определению эксцентриситет параболы считается равным 1: .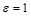

Опр. Парабола имеет одну ось симметрии. Эта ось называется осью параболы. Точка пересечения параболы с осью называется вершиной параболы.

Полярная система координат

Опр. Полярная система координат определяется заданием:

1) точки О – начала координат (полюс);

2) луча 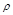, исходящего из полюса (полярная ось);

3) единицей масштаба.

При этом поворот полярной оси вокруг полюса против часовой стрелки считается положительным. Углы измеряются в радианах.

Опр. Полярным радиусом точки М называется расстояние М от полюса: .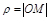

Опр. Полярным углом точки М называется угол поворота 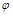полярной оси до совпадения с лучом ОМ.

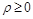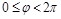Для задания всех точек плоскости достаточно считать, что , а или 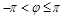. Тогда для каждой точки плоскости, кроме полюса, существует единственная пара полярных координат 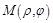. Координаты полюса 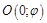, 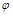имеет любое значение.

Верно и обратное: любая пара значени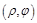й при 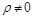определяют единственную точку плоскости. Значение 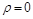задает полюс.

Связь ПСК с ДПСК.

Зададим на плоскости обе системы координат так, чтобы полюс был совмещен с началом ДПСК, ось абсцисс совпадала с полярной осью и единицы масштаба в обеих системах координат имели одинаковую длину. Тогда:

1) если точка М задана полярными координатами 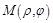, то ее декартовы координаты вычисляются так:

;

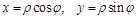2) если известны декартовы координаты точки 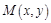, то ее полярные координаты находятся таким образом:

,

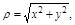
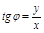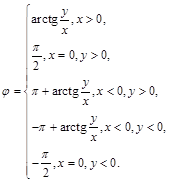
Замечание. Ограничения на полярные координаты 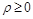, 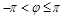не являются существенными и в ряде задач могут быть убраны. Можно считать, что 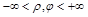. Тогда для построения точки 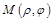в случае 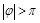делается необходимое число полных оборотов полярного луча вокруг полюса, а при 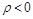от полюса откладывается отрезок длины 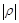на продолжении полярного луча за полюс.