Ең үлкен ортақ бөлгіш және ең кіші ортақ еселік

Қандай санның болса да кем дегенде екі бөлгіші болады – бір саны

және сол санның өзі. Бұл бөлгіштер а санының меншіксіз бөлгіштері деп, ал меншіксіз бөлгіштерінен өзге бөлгіштері меншікті бөлгіштер деп аталады.

Мысалы, 144 санынын меншіксіз бөлгіштерінен өзге меншікті 13 бөлгіші бар, олар 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 47, 72.

санының барлық бөлгіштерінің саны шектеулі, өйткені олардың әрқайсысы а-дан аспайды. а санының барлық бөлгіштерін табу үшін, а санын 1, 2, 3, ... а – 1 сандарының әрқайсысына бөліп көру қажет.

Айталық, мен , бүтін сандары берілсін. Осы екі санның әрқайсысы да бөлінетін 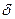санын олардың ортақ бөлгіші деп атайды. мен сандарының әрқайсысының бөлгіштерінің саны ақырлы болғандықтан, олардың ортақ бөлгіштерінің саны да ақырлы.

3-анықтама. Егер сандары мен мен сандарының ортақ бөлгіштері болса, онда олардың ең үлкенін а мен -ның ең үлкен ортақ бөлгіші деп атап келесідей белгілейді

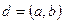
2-теорема. Бүтін сандар сақинасында кез келген екі санның осы сақинаға енетін және де жалғыз тәсілмен анықталатын ең үлкен ортақ бөлгіші болады.

Дәлелдеуі. және сандарының ең үлкен ортақ бөлгіштері екеу делік. Олар 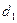саны 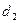-ге бөлінеді. Тура осы сияқты, 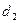-де 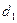санына бөлінеді. Ал 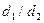және 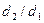қатынастары тек қана 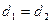немесе 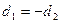болғанда орындалады. ( 9 қасиеттің салдары бойынша). Алда ең үлкен ортақ бөлгіштің тек оң мәндерін қарастырамыз.

Енді, екі санның ең үлкен ортақ бөлгішін табудың жеңіл жолдарының бірі, Евклид алгоратимін қарастырайық.

3-теорема. Егер мен бүтін сандары беріліп,

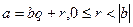(1) болса, онда 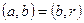. Яғни, мен сандарының ең үлкен ортақ бөлгіші мен r сандарының ең үлкен ортақ бөлгішіне тең.

Дәлелдеуі. (1) теңдіктен мен сандарының ортақ бөлгіші 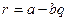санының да бөлгіші екенін және мен r сандарының кез келген ортақ бөлгіші болатынын көреміз. Сондықтан, мен сандарының барлық ортақ бөлгіштері мен r сандарының ортақ бөлгіштері болады, және керісінше. Бұдан мен және мен r сандарының оң ортақ бөлгіштерінің бірдейлігі шығады, демек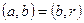

Егер саны -ға қалдықсыз бөлінсе 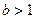болған жағдайда, онда а мен -ның ең үлкен ортақ бөлгіші саны болады,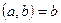

Екі санның ең үлкен ортақ бөлгішін табу үшін, жоғарыдағы теоремаға сүйеніп, «біртіндеп бөлу» әдісін пайдаланады. Бұл әдіс Евклид алгоритмі деп аталады.

3-ші теорема бойынша 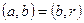. Осы теореманы b мен r сандарына қатысты қарастырып, әрі қарай жалғастырсақ, келесі теңдіктер тізбегін аламыз:

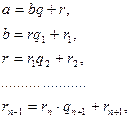
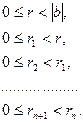
Біз натурал сандарының кемімелі

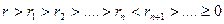
тізбегін алдық. Бұл тізбек ақырсыз болуы мүмкін емес. Сондықтан, жоғарыдағы бөлу процесінде, нольге тең қалдық табылады; 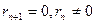болсын.

2-ші теорема бойынша, (2) теңдіктерден, келесі теңдіктерді аламыз:

,

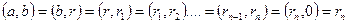яғни, мен сандарының ең үлкен ортақ бөлгіші r 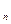-ға тең.

Демек, және бүтін сандарына, Евклид алгоритмін қолдансақ, онда ақырғы нольге тең емес қалдық осы сандардың ең үлкен ортақ бөлгіші болады.

Мысалы, 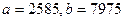сандарының ең үлкен ортақ бөлгішін іздестірейік.

Мунда жазу керек

Ақырғы нольге тең емес қалдық 55, яғни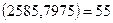

Евклид алгоритмінен кез келген және бүтін сандарының ең үлкен ортақ бөлгішінің бар екенін туындайды. Енді, бірнеше, 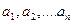сандарының ең ортақ бөлгішінің бар екенін дәлелдейік. Ол үшін, әуелі, келесі теореманы қарастырамыз.

4-теорема. Егер 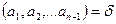және 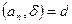болса, онда .

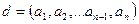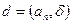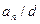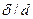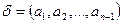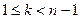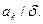
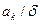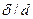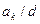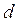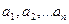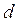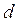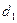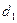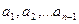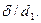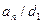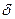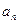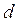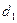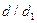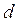Дәлелдеуі. болғандықтан, және . Ал болғандықтан, барлық үшін және болғандықтан . Демек саны сандарының ортақ бөлгіші. Енді -ның осы сандарының ең үлкен ортақ бөлгіші екенін көрсетейік. Ол үшін сандарының -дан өзге ортақ бөлгішін дейік. Онда саны сандарының да ортақ бөлгіші. Сондықтан Ал болғандықтан, және сандарының ең үлкен ортақ бөлгіші - да -ге қалдықсыз бөлінеді: . Біз -ның 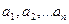сандарының кез келген ортақ бөлгішіне қалдықсыз бөлінетін көрсеттік. Демек.

Салдар. Егер 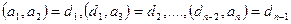болса, онда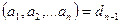

Дәлелдеуі. Дәлелдеуді математикалық индукция әдісімен жүргіземіз. 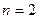болғанда, яғни а₁ және а₂ сандары үшін тұжырым дұрыс 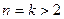үшін тұжырым дәлелденген дейік. Онда 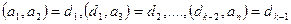болса, дегеннен 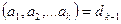екені шығады. Егер 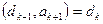болса, онда 3-ші теорема бойынша, 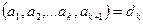екендігі шығады. Демек тұжырым бойынша 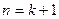үшін де дұрыс. Математикалық индукция бойынша тұжырым барлық 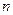үшін дұрыс. Яғни, 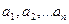сандарының ең үлкен ортақ бөлгішін табу үшін, әуелі 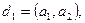содан соң 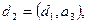т.с.с. 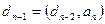-дерді табуымыз керек. Нәтижесінде 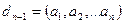аламыз. Мысалы, 988, 2014, 42598, 6726 сандарының ең үлкен ортақ бөлгішін іздестірейік.

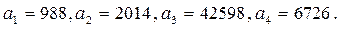Евклид алгоритмі бойынша

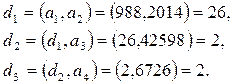
Яғни,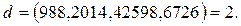

5-теорема. мен сандарының ең үлкен ортақ 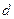бөлгішін сол мен

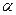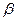сандары арқылы сызықты өрнекпен көрсетуге болады, яғни әр уақытта мен сандары табылып, 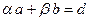болады.

Дәлелдеуі. Евклид алгоритмі бойынша

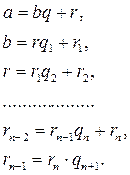
Бірінші теңдіктен 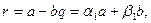мұндағы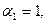 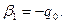Екінші теңдіктен 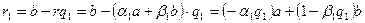= 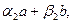мұндағы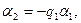 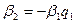бүтін сандар. Осы процесті әрі қарай жалғастыра отырып, 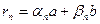теңдігін аламыз. Ал 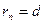екенін ескерсек, 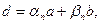мұндағы 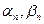- бүтін сандар.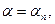 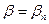деп белгілесек, 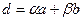теңдігін аламыз. Мысалы, 90 және 35 сандарының ең үлкен ортақ бөлгішін сызықты өрнейік. Евклид алгоритмі бойынша,

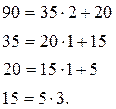
Яғни,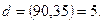

Бірінші теңдіктен 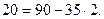Бұл теңдіктің оң жағындағы өрнекті екінші теңдікке қойсақ, онда 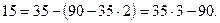Енді 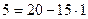теңдігіндегі 20-ны 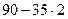мен, ал 15-ті 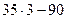мен ауыстырсақ 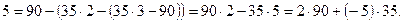Бұл теңдікте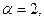

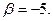
Осы типтес теорема, бірнеше санның ең үлкен ортақ бөлгіші үшін де орындалады, 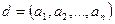болса, онда 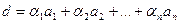болатын 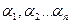-дер табылады.