Математическая модель транспортной задачи

Транспортная задача

ТЗ решает проблему нахождения оптимального (минимального по стоимости) плана распределения и перемещения ресурсов от производителей к потребителям. При решении ТЗ необходимо:

· Обеспечить всех потребителей ресурсами;

· Распределить все произведенные ресурсы;

· Переместить ресурсы от производителей к потребителям с наименьшими затратами.

Пример: Имеется 2 цеха по изготовлению мягких кресел. Производительность первого- 4кресла в сутки, второго – 2 кресла. Имеются 2 магазина, которые продают эти кресла, причем каждый продает ежедневно по 3 кресла. Стоимость перевозки одного кресла от каждого цеха до магазина приведена в таблице.

	Стоимость перевозки	Производители кресел.
				Цех1
				Цех2
Потребители кресел	Магазин 1	Магазин 2

Определить объем поставок кресел от каждого цеха в каждый магазин при минимальной стоимости перевозок.

Задача имеет 3 решения.

Решение 1

Решение 2

Решение 3

Все решения являются допустимыми, надо выбрать наилучшее.

Определим стоимости перевозок при каждом решении.

Решение 1 3*3+4*1+1*0+6*2=25

Решение 2 3*2+4*2+1*1+6*1=21

Решение 3 3*1+4*3+1*2+6*0=17

Решение 3 является оптимальным.

Алгоритм решения ТЗ:

1.Формализация задачи.

2.Приведение к сбалансированному виду.

3.Построение опорного плана

4.Построение оптимального плана.

Для построения опорного плана используется метод «северо-западного и метод минимальных элементов.

Для определения оптимального плана используются методы: распределительный, потенциалов.

Математическая модель транспортной задачи.

От каждогоi производителя произведенный ресурс a_i может перемещаться к j потребителю ресурса в объеме, не превышающем b_j.

Пусть хij – количество груза, перевозимого с i-го в j-й пункт. Через с_ij обозначим стоимость перемещения единицы ресурса от i производителя к j потребителю. Тогда матрица Х будет называться матрицей перевозок, матрица С матрицей стоимости. Предположим, что суммарный объем произведенного ресурса совпадает с объемом потребления ресурса. Суммарная стоимость всех перевозок, вычисленная по любому плану будет 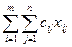Оптимальным планом перевозок будет называться тот из допустимых планов, который обеспечит минимальную сумму затрат на перевозку всех ресурсов. Исходные данные ТЗ задаются вектором произведенных ресурсов А, вектором потребления В и матрицей стоимости С, где I=1,m- число производителей ресурса, j-=1,n число потребителей ресурса. Математическая модель

Целевая функция: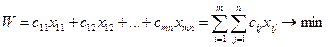

Система ограничений:

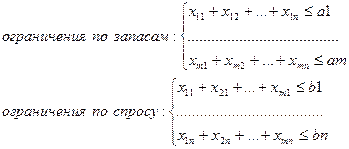
Для решения задачи составляется таблица. В клетки таблицы записывается стоимость соответствующих перевозок C_ij и в них же заносятся значения перевозок xij, удовлетворяющих поставленным ограничениям. Клетки с не нулевыми перевозками называются базисными, а с нулевыми – свободными.