Выполним пункты 6)-8) для степенной модели

Построение степенной модели парной регрессии.

Уравнение степенной модели имеет вид:

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения: .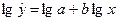

Обозначим 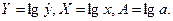Тогда уравнение примет вид: 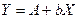, то есть получили линейное уравнение регрессии. Рассчитаем его параметры, используя МНК.

Составим рабочую таблицу.

N		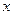X	у	Y	X2	XY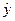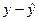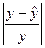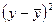
		1,4913		1,5798	2,2240	2,3560	35,2571	-2,7429	7,5235	0,072	0,16
		1,3617		1,4150	1,8542	1,9268	29,0982	3,0982	9,5988	0,119	153,76
		1,5798		1,6020	2,4957	2,5308	40,1901	0,1901	0,0361	0,005	2,56
		1,6721		1,6532	2,7960	2,7643	46,0782	1,0782	1,1625	0,024	43,56
		1,6627		1,7076	2,7646	2,8392	45,4452	-5,5548	30,8558	0,109	158,76
		1,6902		1,6902	2,8568	2,8568	47,3300	-1,67	2,7889	0,034	112,36
		1,3013		1,5315	1,6934	1,9929	26,5965	-7,4035	54,8118	0,218	19,36
		1,5051		1,5440	2,2653	2,3239	35,9845	0,9845	0,9692	0,028	11,56
		1,6627		1,6232	2,7646	2,6989	45,4452	3,4452	11,8694	0,082	12,96
		1,3802		1,3802	1,9050	1,9049	29,9058	5,9058	34,8785	0,246	207,36
∑		15,3071		15,7267	23,6196	24,1945			154,4945	0,937	722,40

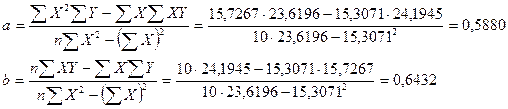
Уравнение регрессии имеет вид:

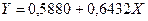
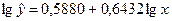
Перейдем к исходным переменным х и у, выполнив потенцирование данного уравнения.

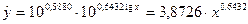
Получим уравнение степенной модели регрессии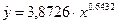

Так как в уравнении степенной регрессии параметр b совпадает с коэффициентом эластичности, то уравнение регрессии можно проинтерпретировать следующим образом: с увеличением полезной площади квартиры на 1% стоимость увеличивается в среднем на 0,6432%.

7)Определим индекс корреляции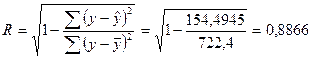

Связь между показателем у и фактором х можно считать достаточно сильной, так как R>0,7. Коэффициент детерминации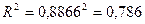

Вариация результативного признака у (стоимость квартиры) на 78,6% объясняется вариацией фактора х (полезной площадью квартиры).

8)Рассчитаем F-критерий Фишера:

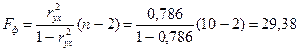
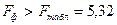для α=0,05; k₁=m=1, k₂=n-m-1=8.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как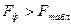

Определим среднюю относительную ошибку аппроксимации:

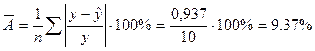
В среднем расчетные значения 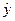для степенной модели отличаются от фактических значений на 9,37%, что находится в пределах нормы, то есть качество модели хорошее.

Выполним пункты 6)-8) для гиперболической модели.

Построение гиперболической модели парной регрессии.

Уравнение гиперболической регрессии: .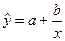

Произведем линеаризацию модели путем замены 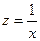. В результате получим линейное уравнение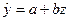

Рассчитаем его параметры по данным следующей рабочей таблицы.

№	Х	у	Z	yz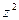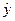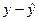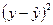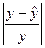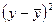
			0,0322581	1,2258065	0,0010406		37,52302	0,4769845	0,2275142	0,01255	0,16
			0,0434783	1,1304348	0,0018904		29,61865	-3,6186452	13,094593	0,13918	153,76
			0,0263158	1,0526316	0,0006925		41,70921	-1,7092116	2,9214042	0,04273	2,56
			0,0212766	0,9574468	0,0004527		45,25921	-0,2592077	0,0671886	0,00576	43,56
			0,0217391	1,1086957	0,0004726		44,93336	6,0666374	36,804089	0,11895	158,76
			0,0204082		0,0004165		45,871	3,1290016	9,7906512	0,06386	112,36
			0,05	1,7	0,0025		25,02423	8,97577	80,564447	0,26399	19,36
			0,03125	1,09375	0,0009766		38,23317	-3,2331738	10,453412	0,09238	11,56
			0,0217391	0,9130435	0,0004726		44,93336	-2,9333626	8,6046162	0,06984	12,96
			0,0416667		0,0017361		30,89487	-6,8948717	47,539255	0,28729	207,36
∑			0,3101318	11,181809	0,0106505		384,0001	-7,894E-05	210,06717	1,09653	722,4

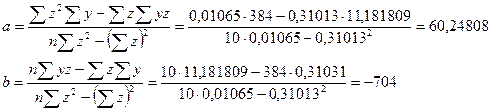
Уравнение регрессии имеет вид:

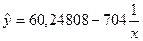
7)Определим индекс корреляции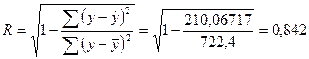

Связь между показателем у и фактором х можно считать достаточно сильной, так как R>0,7

Индекс детерминации: детерминации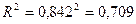

Вариация результативного признака у (стоимости квартиры) на 70,9% объясняется вариацией фактора х (полезной площадью). На остальные факторы, не учтенные в модели, приходится 29,1%.

8)Рассчитаем F-критерий Фишера:

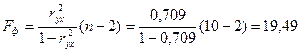
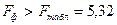для α=0,05; k₁=m=1, k₂=n-m-1=8.

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как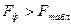

Средняя относительная ошибка:

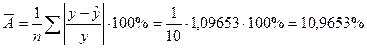
В среднем расчетные значения 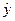для гиперболической модели отличаются от фактических значений у на 10,9653%, что немного выходит за пределы нормы.

Выбор лучшей модели.

Для выбора лучшей модели построим сводную таблицу результатов.

	Коэффициент детерминации R	F-критерий Фишера	Коэффициент (индекс) корреляции	Относительная ошибка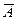
Линейная	0,794	30,83	0,891	9,10
Степенная	0,786	29,38	0,887	9,37
Гиперболическая	0,709	19,49	0,842	10,97

Все модели имеют примерно равные характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации имеет линейная модель. Ее можно взять в качестве лучшей для построения прогноза.

7) X_max=49, следовательно, x_p=49∙0,8=39,2

Рассчитаем доверительный интервал прогноза

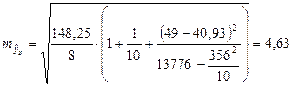
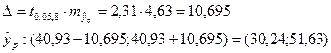
Определим точность прогноза: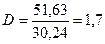

Выполненный прогноз оказался надежным (р=1-α=1-0,05=0,95), но недостаточно точным, так как диапазон верхней и нижней границ составляет 1,7.