Понижение порядка дифференциального уравнения

РАЗДЕЛ 11. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ N –ГО ПОРЯДКА

· Изучаются дифференциальные уравнения n –го порядка

· Рассматриваются линейные уравнения, уравнения с постоянными коэффициентами, вопросы устойчивости

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ N –ГО ПОРЯДКА. ЗАДАЧА КОШИ ДЛЯ УРАВНЕНИЯ .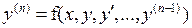

Рассмотрим дифференциальное уравнение n-го порядка, разрешенное относительно n-ой производной:

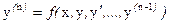(1)

Теорема.Пусть 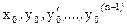- некоторый заданный набор чисел. Пусть функция от 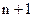переменных 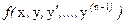обладает следующими свойствами: она непрерывна на совокупности переменных в области ,

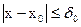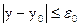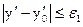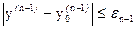, , …, (2)

и пусть частные производные 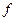по аргументам 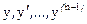ограничены (это, в частности, выполнено, если эти частные производные непрерывны в рассматриваемой области).

Тогда существует такое число 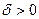и такая функция 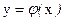, определенная в интервале 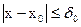, что

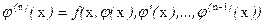(3)

для всех 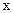из этого интервала, причем

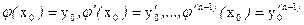(4)

Полученное решение 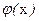зависит от заданных чисел 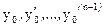. Если считать эти числа изменяющимися параметрами и обозначить 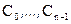, то решение 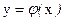уравнения (1), соответствующее такому выбору параметров обозначим 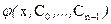и назовём общим решением.

При фиксированных значениях (4) получаем частное решение, или решение задачи Коши с начальными условиями (4). График этого частного решения – интегральная кривая.

Приведём пример решения задачи Коши для уравнения

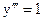(5)

с начальными условиями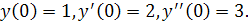

Здесь функция 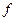тождественно равна 1 и все условия теоремы выполнены в любой точке 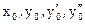. Проинтегрировав уравнение 1 раз, получаем

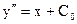(6)

после следующего интегрирования имеем

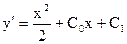(7)

Наконец,

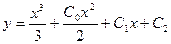(8)

где – произвольные пока постоянные подлежат вычислению

Зададим точку 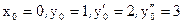: (9)

Тогда, подставляя в (8) 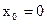находим:

.

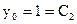Подставив 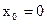в (7), получаем 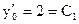, наконец, из (6) получаем .

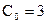Итак, искомое решение с заданными начальными условиями (9) имеет вид .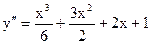

Отметим, что уравнение (5) удовлетворяет всем условиям сформулированной теоремы, поэтому любое его решение получается по формуле (8) при подходящем выборе чисел .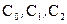

ПОНИЖЕНИЕ ПОРЯДКА ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Дифференциальное уравнение n-го порядка общего вида

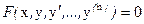(10)

в некоторых случаях может быть сведено к уравнению меньшего порядка.

Случай 1. Уравнение (10) не содержит x, т.е. имеет вид

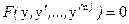(11)

Примем y за независимую переменную, а 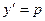– за новую неизвестную функцию. Тогда, по правилу дифференцирования сложной функции,

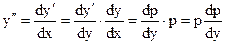, (12)

и, согласно (12),

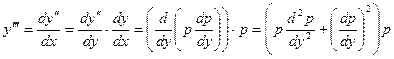(13)

и т.д.

При подстановке найденных значений 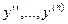в (11) получаем уравнение порядка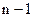

.

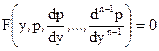Пример. Решить задачу Коши:

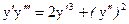, (14)

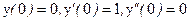
Полагаем 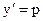, тогда ,

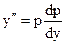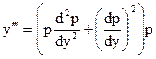
согласно (12) и (13), откуда

,

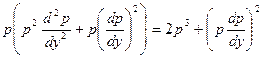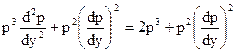
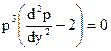
Либо 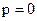, либо

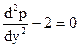. (15)

В первом случае 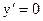, 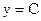- очевидно, решение исходного уравнения, однако не дающее решения задачи Коши (14).

Интегрируя по y обе части уравнения (15), получаем

,

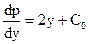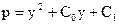. (16)

Из начальных условий:

при 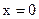, , 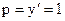а 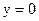, поэтому

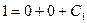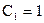, , а так как по (12) , 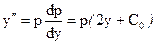, при 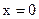имеем, ввиду того, что :

, .

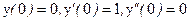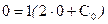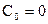Следовательно, (16) принимает вид

,

,

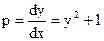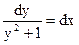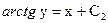
при 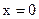, ввиду (14), 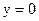, откуда , .

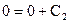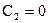В итоге получаем: .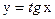

Случай 2. Левая часть (10) не содержит y, т.е.

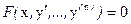
Полагаем 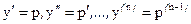и получаем уравнение порядка n-1

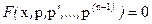
Если же вместе с y отсутствуют и 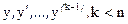, т.е. если

,

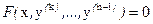то замена 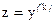даёт уравнение порядка n-k:

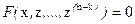
Пример: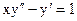

Положим 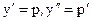. Тогда

, , ,

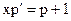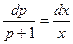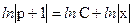считая, что 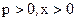, получаем в этой области

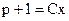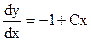, , откуда .

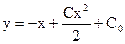Случай 3.

Уравнение (10) – однородное по 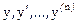, т.е. для любого k 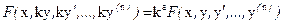(16)

где a – показатель однородности.

Положим

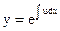
где u – новая неизвестная функция, а под 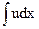понимаем произвольную первообразную. Последовательно находим:

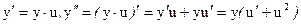и т.д. (17)

Подставляя в уравнение (10) и учитывая (16), получаем:

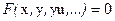
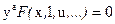
что приводит к дифференциальному уравнению

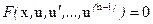
Пример: .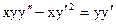

Показатель a однородности по 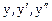равен 2, полагаем 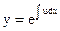и используем формулы (17):

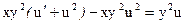или, при 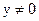(а 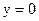, очевидно, решение),

, , , ,

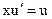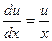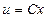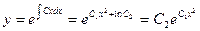где 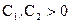- произвольные постоянные.

Если рассмотреть случай 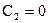, то формула 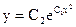и решение .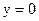