Решение типовых задач ИДЗ №1

Задание № 1.

Даны координаты вершин треугольника : , , .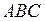

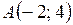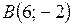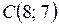Найти:

1) длину стороны ;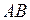

2) уравнения сторон 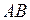и и 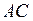их угловые коэффициенты;

3) внутренний угол ;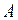

4) уравнение высоты 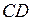и ее длину;

5) уравнение и длину медианы ;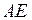

6) уравнение окружности, для которой 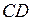служит диаметром;

7) точку пересечения медиан;

8) уравнение прямой, проходящей через точку 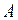, параллельно стороне .

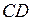Решение.

1) Расстояние между точкам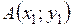и и 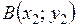определяем по формуле:

.

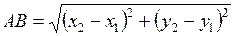Подставляя в нее координаты точек 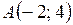и 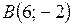, найдем длину стороны :

.

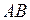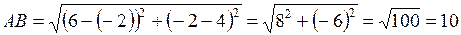2) Уравнение прямой, проходящей через две данные точки 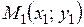и , и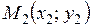меет вид:

.

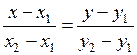Подставив в него координаты точек 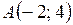и 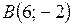, получим уравнение прямой :

,

,

,

,

,

.

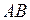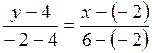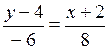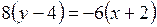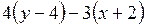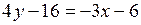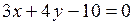Для нахождения углового коэффициента 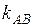прямой 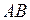разрешим уравнение этой прямой относительно 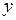, то есть запишем в ви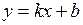де , где 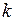– угловой коэффициент:

,

,

.

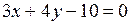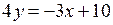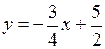Отсюда определяем угловой коэффициент прямой : .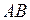

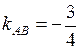Аналогично по двум точкам 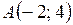и 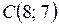, составим уравнение прямой :

,

,

,

,

.

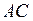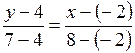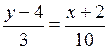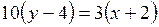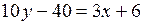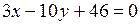Найдем угловой коэффициент 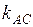прямой :

,

,

.

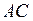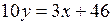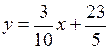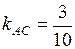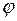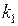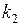3) Угол между двумя прямыми, угловые коэффициенты которых соответственно равны и , находится по формуле:

.

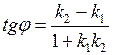Искомый внутренний угол 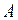образован прямым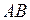и и 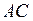, угловые коэффициенты которых 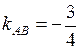, 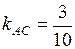. Отмечая на рисунке треугольника 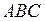в системе координат направление угла 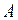против хода часовой стрелки, определяем порядок прямых: 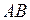–первая, 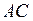– вторая. Следовательно 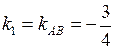, 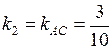. Подставляем угловые коэффициенты в формулу угла между прямыми:

.

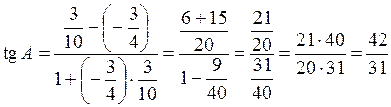Тогда .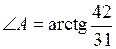

4) Высота 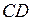перпендикулярна стороне 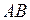, поэтому угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, то есть .

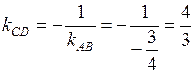Уравнение прямой, проходящей через точку 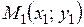в заданном угловым коэффициентом 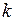направлении, имеет вид:

.

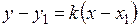Для составления уравнения высоты 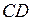, подставим в эту формулу координаты точки 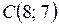и угловой коэффициент :

,

,

,

.

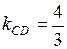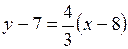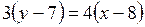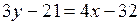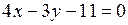Найдем длину высоты 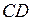, то есть расстояние от точки 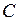до прямой 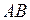. Расстояние от точки 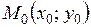до прямой 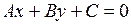находится по формуле:

.

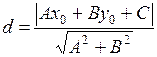Подставим в нее координаты точки 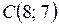и коэффициенты из уравнения прямой : .

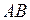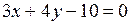Тогда .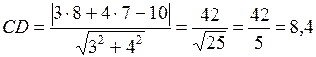

5) Точка 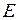– середина отрезка 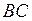. Для определения ее координат применим формулы деления отрезка пополам:

, .

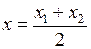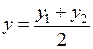Подставляем в них координаты точек 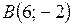и :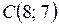

, .

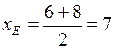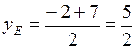То есть .

Найдем длину медианы 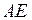, то есть расстояние между точкам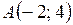и и :

.

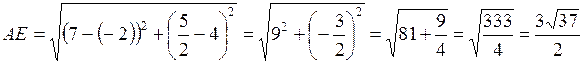6) Точка 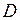– точка пересечения прямых 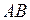и 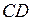. Чтобы найти ее координаты, решим систему уравнений этих прямых:

.

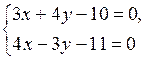Применим правило Крамера:

,

,

,

,

, .

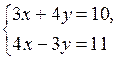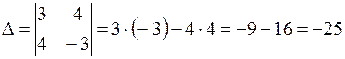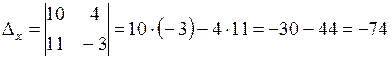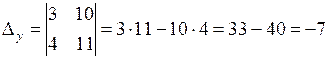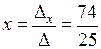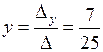Итак, .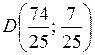

Найдем координаты центра окружности, то есть середину отрезка 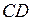, где , :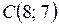

, .

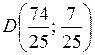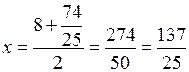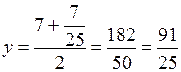Итак, 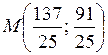– центр окружности.

Радиус окружности 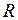равен половине длины отрезка :

.

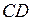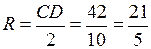Уравнение окружности имеет вид:

,

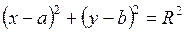где 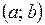– координаты центра окружности; 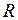– ее радиус.

Подставив в него координаты точк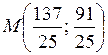и и 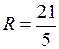, получим уравнение окружности, для которой 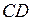является диаметром:

,

.

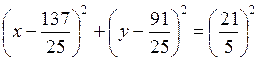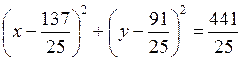7) Точка пересечения медиан делит каждую медиану в отношении 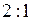, начиная от вершины. Найдем координаты точки 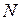, делящей медиану 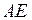в отношении 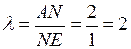. Используем формулы деления отрезка в данном отношении:

, .

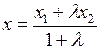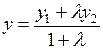Подставим в них координаты точек 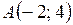, и :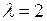

, .

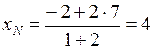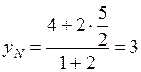Итак, 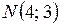– точка пересечения медиан.

8) Составим уравнение прямой 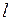, проходящей через точку 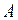, параллельно стороне 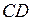. Из условия параллельности прямых 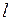и 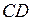следует, что их угловые коэффициенты равны, то есть 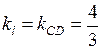. Подставляя в формулу 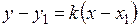координаты точк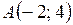и и 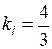, получим уравнение прямой :

,

,

.

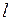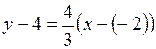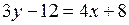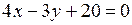При пересечении данных прямых получается треугольник 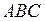(рис. 1).

Рис. 1. Треугольник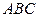

Задание № 2.

Дано уравнение эллипса 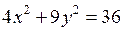. Построить эллипс. Найти полуоси, координаты вершин, фокусов, эксцентриситет.

Решение.

Приведем уравнение эллипса к каноническому виду:

.

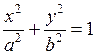Для этого обе части равенства разделим на 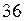и выполним сокращения:

.

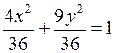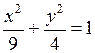– каноническое уравнение эллипса.

Так как 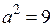, то 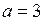– большая полуось, 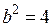, 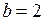– малая полуось.

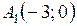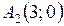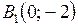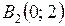, , , – вершины эллипса.

Найдем 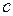– расстояние от центра эллипса до каждого фокуса по формуле связи 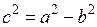, получим 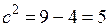, 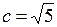. Тогда 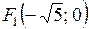, 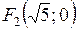– фокусы эллипса.

Эксцентриситет вычислим по формуле 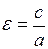, получим .

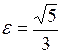По полученным данным можно построить эллипс (рис. 2).

Рис. 2. Эллипс

Задание № 3.

Даны действительная полуось 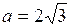и эксцентриситет 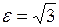гиперболы. Построить гиперболу и найти координаты вершин, фокусов, уравнения асимптот гиперболы.

Решение

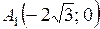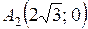, – вершины гиперболы.

Из формулы для нахождения эксцентриситета гиперболы 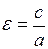найдем значение 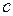– расстояние от центра гиперболы до каждого фокуса:

.

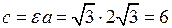Тогда 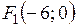, 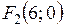– фокусы гиперболы.

Из формулы связи 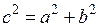найдем мнимую полуось :

,

.

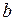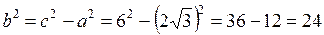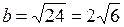Составим каноническое уравнение гиперболы, которое имеет вид:

.

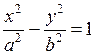Получим .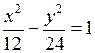

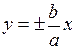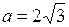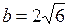Уравнения асимптот гиперболы: . Подставив , и , получим .

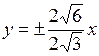После преобразований имеем: 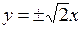– уравнения асимптот данной гиперболы.

Построим гиперболу (рис. 3).

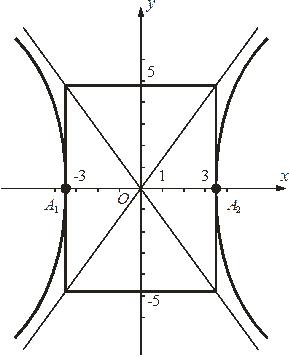
Рис. 3. Гипербола

Задание № 4.

Дано уравнение параболы 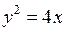. Построить параболу и найти координаты фокуса и уравнение директрисы параболы.

Решение.

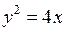– уравнение параболы, с вершиной в начале координат, симметричной относительно оси 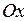, с ветвями, идущими вправо.

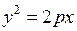– общий вид уравнения такой параболы, где 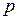– расстояние между фокусом и директрисой.

Из уравнения находим: 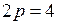, откуда , .

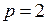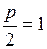Директрисой параболы 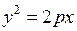является прямая, параллельная оси 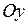, с уравнением 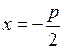, а фокус имеет координаты .

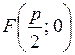Таким образом, для данной параболы директрисой служит прямая 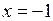, а точка 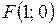– фокусом.

По данным исследования построим параболу (рис. 4).

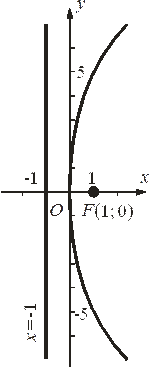
Рис. 4. Парабола

Задание № 5.

Даны координаты точек , , , .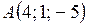

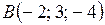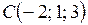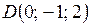Требуется:

1) написать уравнение плоскости ;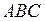

2) написать уравнение плоскости, проходящей через точку 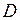параллельно плоскости ;

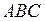3) написать канонические и параметрические уравнения прямой ;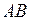

4) написать канонические уравнения прямой, проходящей через точку 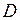перпендикулярно плоскости ;

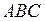5) найти расстояние от точки 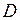до плоскости .

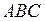Решение.

1) Уравнение плоскости, проходящей через три точки 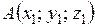, , 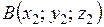, 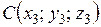имеет вид:

.

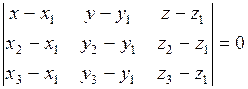Подставим в него координаты точек , , :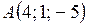

,

,

,

,

,

.

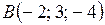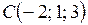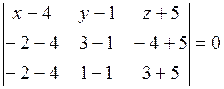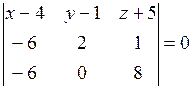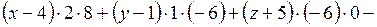
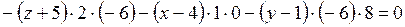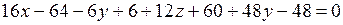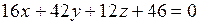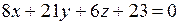Таким образом, 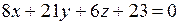– уравнение плоскости .

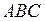2) Для составления уравнения плоскости 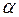, проходящей через точку 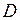параллельно плоскости 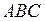, найдем координаты ее нормального вектора, в качестве которого можно взять нормальный вектор плоскости 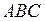в силу их параллельности.

Если общее уравнение плоскости имеет вид 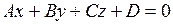, то ее нормальный вектор имеет координаты .

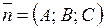Для плоскости 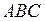с уравнением 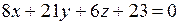нормальным вектором является вектор 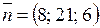. Он же служит и нормальным вектором для плоскости .

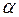Если плоскость проходит через точку 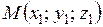перпендикулярно нормальному вектору 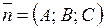, то ее уравнение имеет вид:

.

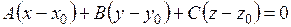Подставим в него координаты точки 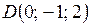и нормального вектора :

,

,

.

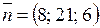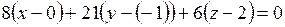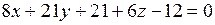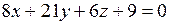Таким образом, 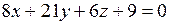– уравнение плоскости 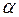, проходящей через точку 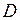параллельно плоскости .

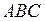3) Канонические уравнения прямой, проходящей через две данные точки 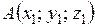, , 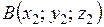имеют вид:

.

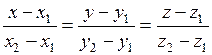Подставив в них координаты точек 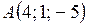и 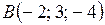, получим канонические уравнения прямой :

,

.

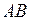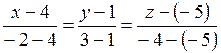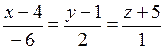От канонических уравнений прямой 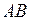, введя параметр 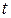, перейдем к ее параметрическим уравнениям:

,

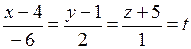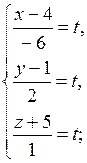
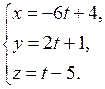
4) Составим канонические уравнения прямой 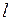, проходящей через точку 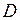перпендикулярно плоскости 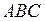. В качестве направляющего вектора 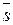прямой 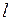можно взять нормальный вектор перпендикулярной ей плоскости 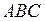, то есть .

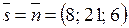Если прямая проходит через точку 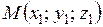параллельно направляющему вектору , то ее канонические уравнения имеют вид:

.

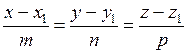Подставив в них координаты точки 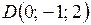и направляющего вектора 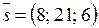, получим канонические уравнения прямой 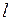, проходящей через точку 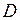перпендикулярно плоскости :

,

.

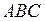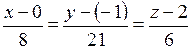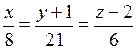5) Расстояние от точки 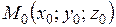до плоскостис уравнением 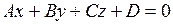находим по формуле:

.

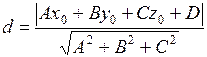Подставим в нее координаты точки 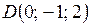и коэффициенты из уравнения плоскости :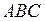

.

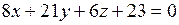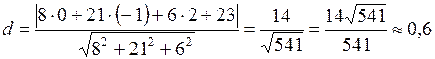Таким образом, расстояние от точки 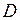до плоскости 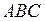равно 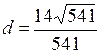.