Використання математичних методів у дослідженнях
Лекція № 5. Математичні методи
Вирішення практичних завдань математичними методами послідовно здійснюється шляхом математичного формулювання завдання (розробки математичної моделі), вибору методу проведення дослідження отриманої математичної моделі, аналізу отриманого математичного результату.
Математичне формулювання завдання зазвичай представляється у вигляді чисел, геометричних образів, функцій, систем рівнянь і тому подібне. Опис об'єкту (явища) може бути представлений за допомогою неперервної або дискретної, детермінованої або стохастичної та іншими математичними формами.
Математична модель є системою математичних співвідношень - формул, функцій, рівнянь, систем рівнянь, що описують ті або інші сторони об'єкту, що вивчається, явища, процесу.
Першим етапомматематичного моделювання є постановка завдання, визначення об'єкту і цілей дослідження, задання критеріїв (ознак) вивчення об'єктів і управління ними. Неправильна або неповна постановка завдання може звести нанівець результати всіх подальших етапів.
Вельми важливим на цьому етапі є встановлення меж області впливу об'єкту, що вивчається. Межі області впливу об'єкту визначаються областю значущої взаємодії із зовнішніми об'єктами. Дана область може бути визначена на основі наступних ознак: межі області охоплюють ті елементи, дія яких на досліджуваний об'єкт не дорівнює нулеві; за цими межами дія досліджуваного об'єкту на зовнішні об'єкти прямує до нуля. Урахування області впливу об'єкту при математичному моделюванні дозволяє включити в цю модель всі істотні чинники і розглядати модельовану систему як замкнуту, тобто з відомим ступенем наближення, незалежну від зовнішнього середовища. Останнє значно спрощує математичне дослідження.
Наступним етапом моделювання є вибір типу математичної моделі. Вибір типу математичної моделі є найважливішим моментом, що визначає напрям всього дослідження. Зазвичай послідовно будується декілька моделей. Порівняння результатів їх дослідження з реальністю дозволяє встановити найкращу з них.
На етапі вибору типу математичної моделі за допомогою аналізу даних пошукового експерименту встановлюються: лінійність або нелінійність, динамічність або статичність, стаціонарність або нестаціонарність, а також степінь детермінованості досліджуваного об'єкту або процесу.
Лінійність встановлюється за характером статичної характеристики досліджуваного об'єкту. Під статичною характеристикою об'єкту розуміється зв'язок між величиною зовнішньої дії на об'єкт (величиною вхідного сигналу) і максимальною величиною його реакції на зовнішню дію (максимальною амплітудою вихідної характеристики системи). Під вихідною характеристикою системи розуміється зміна вихідного сигналу системи в часі. Якщо статична характеристика досліджуваного об'єкту виявляється лінійною, то моделювання цього об'єкту здійснюється з використанням лінійних функцій. Нелінійність статичної характеристики і наявність запізнювання в реагуванні об'єкту на зовнішню дію є яскравими ознаками нелінійності об'єкту. В цьому випадку для його моделювання повинна бути прийнята нелінійна математична модель.
Застосування лінійної математичної моделі значно спрощує її подальший аналіз, оскільки така модель дозволяє користуватися принципом суперпозиції. Принцип суперпозиції стверджує, що коли на лінійну систему впливають одночасно декілька вхідних сигналів, то кожен з них фільтрується системою так, ніби ніякі інші сигнали на неї не діють. Загальний вихідний сигнал лінійної системи за принципом суперпозиції утворюється в результаті підсумовування її реакції на кожен вхідний сигнал.
Встановлення динамічності або статичності здійснюється за поведінкою досліджуваних показників об'єкту у часі. Стосовно детермінованої системи можна говорити про статичність або динамічність по характеру її вихідної характеристики. Якщо середнє арифметичне значення вихідного сигналу на різних відрізках часу не виходить за допустимі межі, що визначені точністю методики вимірювання досліджуваного показника, то це свідчить про статичність об'єкту. Стосовно ймовірнісних систем їх статичність встановлюється по мінливості рівня їх відносної організації. Якщо мінливість цього рівня не перевищує допустимі межі, то система визначається як статична.
Вельми важливим є вибір відрізків часу, на яких встановлюється статичність або динамічність об'єкту. Якщо об'єкт на малих відрізках часу виявився статичним, то при збільшенні цих відрізків результат не зміниться. Якщо ж статичність встановлена для великих відрізків часу, то при їх зменшенні результат може змінитися і статичність об'єкту може перейти в динамічність.
При виборі типу (класу) моделі ймовірнісного об'єкту важливим є встановлення його стаціонарності. Зазвичай про стаціонарність або нестаціонарність ймовірнісних об'єктів судять за зміною в часі параметрів законів розподілу випадкових величин. Частіш за все, для цього використовують середнє арифметичне 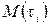 і середнє квадратичне відхилення випадкових величин
і середнє квадратичне відхилення випадкових величин 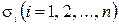 від середнього арифметичного та середнього квадратичне відхилення у часі.
від середнього арифметичного та середнього квадратичне відхилення у часі.
З ряду середніх арифметичних 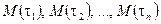 вибирається мінімальне значення
вибирається мінімальне значення 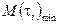 і будується інтервал з межами
і будується інтервал з межами
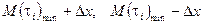 ,
,
де 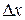 - величина, що характеризує точність методики вимірювання досліджуваного показника.
- величина, що характеризує точність методики вимірювання досліджуваного показника.
Якщо всі значення 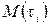 укладаються в цей інтервал, то об'єкт визначається як стаціонарний за середнім арифметичним
укладаються в цей інтервал, то об'єкт визначається як стаціонарний за середнім арифметичним 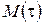 .
.
Аналогічно визначається стаціонарність за середнім квадратичним відхиленням.
Граничні значення 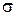 при встановленні стаціонарності визначаються за формулами
при встановленні стаціонарності визначаються за формулами
 ,
,
де
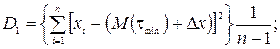
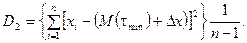
Тут 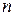 - число спостережень.
- число спостережень.
Якщо всі значення 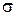 укладаються в інтервал
укладаються в інтервал 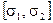 , то об'єкт вважається стаціонарним. Інакше об'єкт визначається як ймовірнісний нестаціонарний, навіть якщо величина середнього арифметичного М не змінюється в часі.
, то об'єкт вважається стаціонарним. Інакше об'єкт визначається як ймовірнісний нестаціонарний, навіть якщо величина середнього арифметичного М не змінюється в часі.
Встановлення загальних характеристик об'єкту дозволяє підібрати математичний апарат, на базі якого будується математична модель. Вибір математичного апарату може бути здійснений відповідно до схеми, представленої на рис. 5.1. Як видно з даної схеми, вибір математичного апарату не є однозначним і жорстким.
Так, для детермінованих об'єктів може використовуватися апарат лінійної і нелінійної алгебри, теорії диференціальних і інтегральних рівнянь, теорії автоматичного регулювання.
Адекватним математичним апаратом для моделювання ймовірнісних об'єктів є теорія детермінованих і випадкових автоматів з детермінованими і випадковими середовищами, теорія випадкових процесів, теорія марковських процесів, евристичне програмування, методи теорії інформації, методи теорії управління і оптимальні моделі.
При описі квазідетермінованих (ймовірнісно-детермінованих) об'єктів може використовуватися теорія диференціальних рівнянь з коефіцієнтами, що підпорядковані певним законам.
Мета і завдання, які ставляться при математичному моделюванні, відіграють важливу роль при виборі типу (класу) моделі. Практичні завдання вимагають простого математичного апарату, а фундаментальні - складнішого, допускають проходження ієрархії математичних моделей, починаючи від чисто функціональних і кінчаючи моделями, що використовують строго встановлені
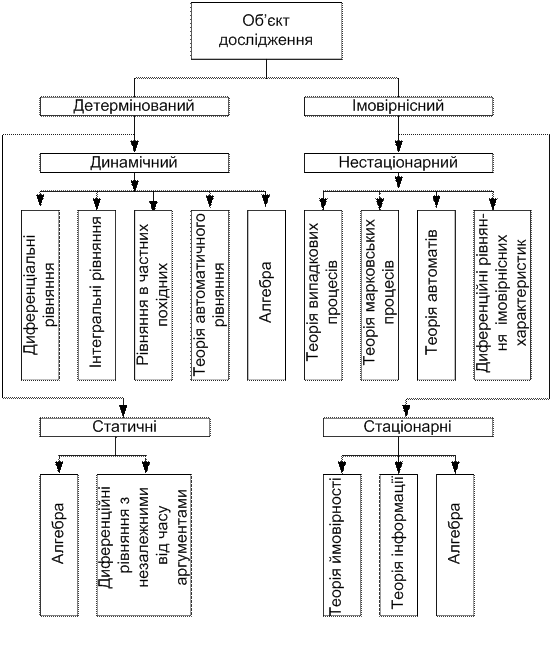
Рис. 5.1. Математичний апарат для побудови математичної моделі
закономірності і структурні параметри.
Не менше значення для вибору моделі має аналіз інформаційного масиву, отриманого як результат аналітичного огляду результатів досліджень інших авторів або пошукового експерименту. Розділення масиву на залежні і незалежні чинники, на вхідні і вихідні змінні, попередній пошук взаємозв'язку між різними даними вибірки дозволяє визначити адекватний математичний апарат.
Аналіз інформаційного масиву дозволяє встановити неперервність або дискретність досліджуваного показника і об'єкту в цілому.
У неперервних об'єктах всі сигнали є неперервними функції часу. У дискретних об'єктах всі сигнали квантуються за часом і амплітуді. Якщо сигнали квантуються тільки за часом, тобто представляються у вигляді імпульсів з відповідною амплітудою, то такі об'єкти називають дискретно-неперервними.
Встановлення неперервності об'єкту дозволяє використовувати для його моделювання диференціальні рівняння. У свою чергу, дискретність об'єкту зумовлює використання для математичного моделювання апарату теорії автоматів.
Окрім вищевикладеного на встановлення типу (класу) математичної моделі може істотно вплинути необхідність певного відображення гіпотези.
Врахування цілей і завдань математичного моделювання, характеру гіпотези і аналізу інформаційного масиву дозволяє конкретизувати модель, тобто у вибраному типі (класі) моделей визначити їх вид. Вибір виду математичної моделі в даному їх класі є третім етапом математичного моделювання. Даний етап пов'язаний із визначенням областей означення досліджуваних параметрів об'єкту, тобто значення, які є допустимими, і встановленням залежностей між ними. Для кількісних (числових) параметрів залежності задаються у вигляді систем рівнянь (алгебричних або диференціальних), для якісних - використовуються табличні способи задання функцій.
Якщо параметри описуються суперечливими залежностями, то визначаються їх вагові коефіцієнти, виражені в долях одиниці, балах. Тим самим суперечливі залежності переводяться в імовірнісні.
Для опису складних об'єктів з великою кількістю параметрів можливе розбиття об'єкту на елементи (підсистеми), встановлення ієрархії елементів і опис зв'язків між ними на різних рівнях ієрархії.
Особливе місце на етапі вибору виду математичної моделі займає опис перетворення вхідних сигналів у вихідні характеристики об'єкту.
Якщо на попередньому етапі було встановлено, що об'єкт є статичним, то побудова функціональної моделі здійснюється за допомогою рівнянь алгебри. При цьому окрім простих алгебричних залежностей використовуються регресійні моделі і системи алгебричних рівнянь.
Якщо заздалегідь відомий характер зміни досліджуваного показника, то кількість можливих структур алгебричних моделей різко скорочується і перевага віддається тій структурі, яка відображає найбільш загальну закономірність або загальновідомий закон. Якщо характер зміни досліджуваного показника заздалегідь невідомий, то ставиться пошуковий експеримент. Перевага віддається тій математичній формулі, яка дає якнайкращий збіг з даними пошукового експерименту.
Результати пошукового експерименту і апріорний інформаційний масив дозволяють встановити схему взаємодії об'єкту із зовнішнім середовищем за співвідношенням вхідних і вихідних величин. В принципі можливе встановлення чотирьох схем взаємодії:
─ одновимірно-одновимірна схема (рис. 5.2, а) - на об'єкт впливає тільки один фактор і його поведінка розглядається теж лише за одним показником (один вихідний сигнал);
─ одновимірна - багатовимірна схема (рис. 5.2, б) - на об'єкт впливає один фактор, а його поведінка оцінюється за декількома показниками;
─ багатовимірно-одновимірна схема (рис. 5.2, в) - на об'єкт впливає декілька факторів, а його поведінка оцінюється за одним показником;
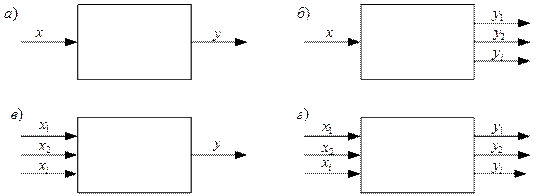
Рис. 5.2. Схеми взаємодії об'єкту із зовнішнім середовищем
─ багатовимірно-багатовимірна схема (рис. 5.2, г) - на об'єкт впливає декілька факторів і його поведінка оцінюється за кількома показниками.
При одновимірно-одновимірній взаємодії статичного стаціонарного детермінованого об'єкту із зовнішнім середовищем постійна вхідна дія зв'язується з постійним вихідним сигналом через постійний коефіцієнт. Якщо ж цей об'єкт є нестаціонарним, то вказаний зв'язок описується різними функціями 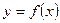 . Найчастіше такі функціональні залежності описуються поліномами.
. Найчастіше такі функціональні залежності описуються поліномами.
У разі виявлення багатовимірно-одновимірної схеми статичний стаціонарний детермінований об'єкт описується наступною моделлю:
при рівнозначності зовнішніх впливів
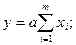
при нерівнозначності зовнішніх впливів
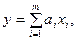
де 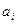 - постійний коефіцієнт; m - число зовнішніх впливів (факторів).
- постійний коефіцієнт; m - число зовнішніх впливів (факторів).
Для статичного нестаціонарного об'єкту (при тій же схемі взаємодії) часто використовується модель у вигляді повного степеневого полінома:
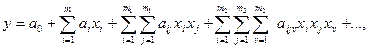
де 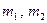 - кількість парних і потрійних поєднань вхідних факторів (
- кількість парних і потрійних поєднань вхідних факторів ( 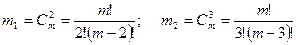 ).
).
При одновимірно-багатовимірній схемі статичний стаціонарний і нестаціонарний об'єкт описується аналогічно одновимірно-одновимірній схемі взаємодії статичного стаціонарного об'єкту із зовнішнім середовищем. При цьому визначаються окремо математичні моделі вхідної дії з кожним вихідним сигналом. Вихідні сигнали вважаються незалежними.
Багатовимірно-багатовимірна взаємодія зводиться до багатовимірно-одновимірної і математична модель об'єкту приймається аналогічною наведеній вище. Для нестаціонарної одновимірно-одновимірної (багатовимірної) взаємодії алгебричні функції можуть бути розв’язками відповідних диференціальних рівнянь. При цьому необхідно розглядати похідні математичного сподівання за змінним фактором. Наприклад, експоненційна залежність може бути розв’язком наступного диференціального рівняння:
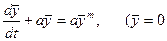 при
при 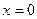 ),
),
де 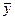 - максимальне значення математичного сподівання.
- максимальне значення математичного сподівання.
Вибір виду моделі динамічного об'єкту зводиться до складання диференціальних рівнянь. Модель динамічного об'єкту, може бути побудована і в класі алгебричних функцій. Проте такий підхід є обмеженим, оскільки не дозволяє в математичному описі врахувати дію вхідних впливів вхідних дій на динаміку виходу без істотної перебудови самих алгебричних функцій (структури і коефіцієнтів):
Тому за повнотою моделі віддається перевага математичним моделям, побудованим у класі диференціальних рівнянь.
Якщо змінні, що цікавлять дослідника, є лише функціями часу, то для моделювання використовуються звичайні диференціальні рівняння. Якщо ж ці змінні є також функціями просторових координат, то для опису таких об'єктів недостатньо звичайних і слід використовувати більш складні диференціальні рівнянням, а саме диференціальні рівняння в частинних похідних.
Методологія моделювання динамічних систем в класі диференціальних рівнянь істотно залежить від схеми взаємодії об'єкту з середовищем і степені знання входу і виходу об'єкту.
Розглянемо випадок, коли вхід і вихід об'єкту відомі.
При одновимірно-одновимірній і одновимірно-багатовимірній взаємодії детермінованого об'єкту з середовищем структура диференціального рівняння визначається за виглядом вихідної характеристики об'єкту для типового вхідного впливу (наприклад, ступінчастого) .
Однєю з найбільш простих вихідних характеристик об'єкту, є лінійна (рис. 5.3, а). Така зміна виходу визначається розв’язком диференціального рівняння
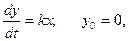
де 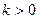 - коефіцієнт розмірності і пропорційності;
- коефіцієнт розмірності і пропорційності; 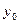 - початкове значення вихідного сигналу; t - час.
- початкове значення вихідного сигналу; t - час.
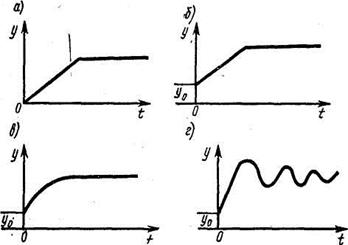
Рис. 6.3. Вихідні характеристики детермінованого об'єкту при ступінчастій зовнішній дії
Якщо 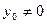 , то вихідна характеристика об'єкту відповідає рис.5.3, б. Проте диференціальне рівняння залишається незмінним.
, то вихідна характеристика об'єкту відповідає рис.5.3, б. Проте диференціальне рівняння залишається незмінним.
Складніший вид реакції об'єкту на ступінчастий вхідний вплив (рис. 5.3, в) може бути описаний повним неоднорідним диференціальним рівнянням першого порядку:
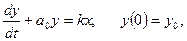
де 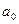 - коефіцієнт диференціального рівняння.
- коефіцієнт диференціального рівняння.
Реакція об'єкту, що відповідає рис. 5.3, г, дозволяє використовувати як математичну модель об'єкту диференціальне рівняння другого порядку:
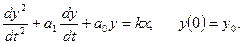
Розглянуті види математичних моделей відповідають постійному впливу 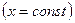 . Якщо вхідні впливи є деякими функціями часу, зокрема алгебричними, то в наведених диференціальних рівняннях у правій частини виконується заміна
. Якщо вхідні впливи є деякими функціями часу, зокрема алгебричними, то в наведених диференціальних рівняннях у правій частини виконується заміна 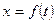 .
.
При багатовимірно-одновимірній взаємодії (у разі детермінованого об'єкту) динамічні моделі також знаходять у класі диференціальних рівнянь. При цьому допускається, що вхідні фактори є незалежними за їх дією на об'єкт. Всі фактори зводяться до суми коефіцієнтами чутливості у правій частині диференціального рівняння. Диференціальне рівняння підбирається за виглядом вихідної характеристики об'єкту.
Якщо припущення про незалежність впливів факторів невірне, то заздалегідь встановлюється вплив кожного з факторів на вихідний показник об'єкту і за виглядом вихідних характеристик підбираються відповідні диференціальні рівняння. При одночасній дії факторів вважається, що вихідна характеристика об'єкту є сумою розв’язків незалежних диференціальних рівнянь, кожен з яких відповідає окремому фактору.
Для багатовимірно-багатовимірної взаємодії побудова динамічних моделей може бути зведене до багатовимірно-одновимірної схеми взаємодії.
За відсутності апріорної інформації про вхід і вихід об'єкту диференціальні рівняння, що моделюють динаміку об'єкту, складаються на основі припущень або знань про властивості і структуру об'єкту.
