В ответе укажите номер верного ответа.

ИНСТРУКЦИЯ

ПО ПРОВЕДЕНИЮ КОНТРОЛЬНОЙ ДИАГНОСТИЧЕСКОЙ

РАБОТЫ (КДР) № 2

ПО МАТЕМАТИКЕ В 8 КЛАССАХ

ТЕМА: Повторение курса математики 5 - 7 и 8 (1 полугодие) классов

Цель работы:

-отследить уровень усвоения учащимися основных тем школьного курса математики 5 – 7 классов и 8 класс (1 полугодие: геометрия до теоремы Пифагора и алгебра до свойств квадратного корня (включительно))

- планомерная подготовка к ОГЭ 2016 по математике.

Задачи:

● психологическая подготовка учащихся к новой форме итоговой аттестации;

● выявление пробелов учащихся;

● анализ ошибок и определение системы методических рекомендаций, которые помогут в улучшении качества подготовки к ОГЭ 2016 по математике.

Сроки проведения: с 15 по 21 декабря2015 г.

Срок сдачи анализа работы: отчет сдавать не надо.

Структура работы:

Вариант работы состоит из 2–х частей, которые содержат задания из открытого банка задач по подготовке к ГИА по математике (mathgia.ru). Задания первой части выполняются с краткой записью ответа или выбором правильного ответа. Задания второй части предусматривают полное решение с записью ответа и расположены по нарастанию сложности. Использование калькулятора запрещается. Можно использовать справочные материалы, только утвержденные ФИПИ (см. демоверсию 2016)

Данная работа рассчитана на 90 – 120 минут (2 урока + 2 переменки).

Система оценивания работы:

1. За верное выполнение заданий части 1 (1 – 12) учащийся получает 1 балл.

2. За любое неверное выполнение задания части 1 - 0 баллов.

3. Оценивание заданий 2 части:

- за верное и обоснованное решение заданий № 13 или № 15, учащийся получает 2 балла;

- за верное и обоснованное решение заданий № 14 или № 16, учащийся получает 3 балла;

- за не грубую (вычислительную) ошибку или описку учащийся получает минус 1 балл (подробно см. критерии оценивания заданий 2 части).

4. Максимальный балл за всю работу – 22 балла

5. Работа носит рекомендательный, но желательный, характер. Рекомендуем работу проводить на бланках ОГЭ.

КДР – 8 – 2

Вариант 1

Часть 1

При выполнении заданий этой части необходимо дать краткий ответ (задания 1-12), ответом является целое число или конечная десятичная дробь. Наименования писать не нужно.

Модуль «Алгебра»

1. Товар на распродаже уценили на 10%, при этом он стал стоить 900 р. Сколько стоил товар до распродажи?

2. Расположите в порядке возрастания числа: 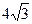, , 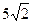6.

В ответе укажите номер верного ответа.

3. Решите уравнение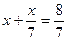

4. Решить неравенство 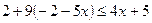. В ответе укажите наименьшее целое решение.

5. Вычислите координаты точки пересечения прямых 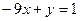и 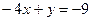. В ответ запишите сумму абсциссы и ординаты точки пересечения прямых.

6. Най­ди­те зна­че­ние вы­ра­же­ния .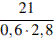

7. На ко­ор­ди­нат­ной пря­мой от­ме­че­ны числа p, q и r.

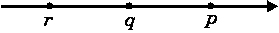Какая из раз­но­стей p − r, p − q, r − q от­ри­ца­тель­на?

1) p – r; 2) p – q; 3) r – q; 4) ни одна из них.В ответ укажите номера верных ответов без знаков препинания и пробелов.

8. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида у = kх + b. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и зна­ка­ми ко­эф­фи­ци­ен­тов k и b.

А	Б	В

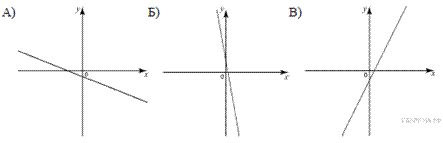
1) k < 0, b < 0; 2) k > 0, b > 0; 3) k < 0, b > 0; 4) k > 0, b < 0. Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке.

9. Упро­сти­те вы­ра­же­ние 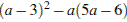, най­ди­те его зна­че­ние при 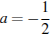. В ответ за­пи­ши­те по­лу­чен­ное число.

Модуль «Геометрия»

10. Какое из ниже перечисленных утверждений является верным:

1) В параллелограмме противоположные углы равны.

2) Сумма углов в выпуклом четырехугольнике не больше 180º.

3) При пересечении двух прямых смежные углы всегда равны.

4) Если сторона и два угла одного треугольника соответственно равны стороне и двум

углам другого треугольника, то такие треугольники равны

5) Площадь трапеции равна произведению суммы ее оснований на половину высоты

этой трапеции.