Деревья, остовы, разрезы
Кафедра «Математика и математические методы в экономике»
А.Л. Пирозерский
Л.П. Пирозерская
МАТЕМАТИКА
Основы ДИСКРЕТНОЙ МАТЕМАТИКИ
Методические указания по изучению курса
Санкт-Петербург
Одобрены на заседании кафедры «Математика и математические методы в экономике», протокол №10 от 07.05.2002 г.
Утверждены Методическим Советом ИЭУПС, протокол №24 от 28.05.2002 г.
Математика. Основы дискретной математики.Методические указания по изучению курса. – СПб.: Изд-во СПбГАСЭ, 2004. – 39 с.
В работе рассмотрены основные понятия теории графов и её приложения к исследованию линейных систем и задачам минимизации и сетевого планирования. Рассмотрены с подробными объяснениями примеры решения задач различной сложности. Имеются задачи для самостоятельной работы.
Данные методические указания предназначены для самостоятельной работы студентов всех специальностей дневной и заочной форм обучения.
Составители: канд. физ.-мат. наук, доц. А.Л. Пирозерский;
ст. преп. Л.П. Пирозерская
Рецензент: ст. преп. И.Ю. Попова
Ó Санкт-Петербургская государственная академия сервиса и экономики
2004 г.
Содержание
Основные понятия и определения.. 4
Деревья, остовы, разрезы... 5
Ориентированные графы... 7
Уравнения и графы... 9
§5. Правила упрощения орграфов
для систем уравнений.. 11
Построение нормализованного графа.. 16
§7. Задача о кратчайшем пути на графе.
Алгоритм Дейкстры... 21
§8. Сетевое планирование.. 25
Задачи для самостоятельной работы... 35
Литература.. 39
Основные понятия и определения
Графомназывается совокупность точек, называемых вершинами, и соединяющих их линий, которые называются ребрами. На рис. 1 изображен граф, у которого 5 вершин и 7 ребер.
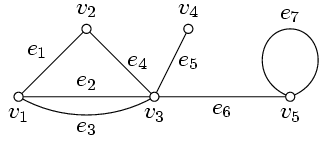 Рис. 1. Рис. 1. | 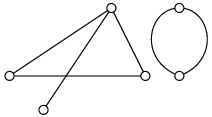 Рис. 2. Рис. 2. |
Ребра, имеющие одинаковые концевые вершины, называются параллельными (e2. e3 на рис.1). Ребро, концевые вершины которого совпадают, называется петлей (e7 на рис.1). Вершина и ребро называются инцидентными друг другу, если вершина является для этого ребра концевой точкой. Две вершины, являющиеся концевыми для некоторого ребра, называются смежными вершинами. Два ребра, инцидентные одной и той же вершине, называются смежными ребрами. Например, на рис. 1, вершина v3 и ребро e6 инцидентны друг другу, v1 и v2 – смежные вершины, e5 и e2 – смежные ребра.
Граф называется полным, если любые две его различные вершины соединены ребром, и он не содержит параллельных рёбер.
Маршрутом в графе называется последовательность ребер, ведущая от некоторой начальной вершины vi в конечную вершину vj, в которой каждые два соседних ребра имеют общую вершину. Маршрут называется путем, если все составляющие его ребра различны. Например, в графе, изображенном на рис. 1, последовательность ребер (e1, e4, e3, e2, e6, e7) образует путь, ведущий от вершины v1 к вершине v5. Циклом называется путь, начальная и конечная вершины которого совпадают. На рис. 1 ребра (e1, e4, e2) образуют цикл. Путь (цикл) называется простым, если он не проходит ни через одну вершину более одного раза. Длиной пути (цикла) называется число содержащихся в нем рёбер.
Граф называется связным, если для любых двух его вершин существует путь, их соединяющий. В противном случае граф называется несвязным. Любой несвязный граф Гявляется совокупностью связных графов, обладающих тем свойством, что никакая вершина одного из них не связана путем ни с какой вершиной другого. Каждый из таких графов называется компонентой графа Г. Граф, изображенный на рис. 1, является связным, а на рис. 2 – несвязный и состоит из 2 компонент.
Рассмотрим граф Г=(V,E) с множеством вершин V и множеством ребер E. Граф Г'=(V', E') называется подграфом графа Г, если V' и E' являются подмножествами V и E, причем ребро содержится в E' только в том случае, если его концевые вершины содержатся в V'.
Эйлеровым путем (циклом) графа называется путь (цикл), содержащий все ребра графа ровно один раз. Граф, обладающий эйлеровым циклом, называется эйлеровым графом. Можно доказать, что граф является эйлеровым тогда и только тогда, когда он связен и все его вершины имеют четную степень.
Гамильтоновым путем (циклом) графа называется путь (цикл), проходящий через каждую вершину в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым. Достаточным условием гамильтоновости является полнота графа.
Деревья, остовы, разрезы
Деревом называется связный граф, не содержащий циклов. Граф, не имеющий циклов и состоящий из k компонент, называется лесом из k деревьев. Можно показать, что граф Гс n вершинами является деревом тогда и только тогда, когда он связен ичисло егоребер равно (n—1).
Деревом некоторого графа Г называется его связный подграф без циклов. Дерево графа Г, содержащее все его вершины, называется остовом графа Г или его покрывающим деревом. Выбор остова графа в общем случае неоднозначен; например, граф, приведенный на рис. 1, имеет несколько остовов, три из которых показаны на следующем рисунке:

Если остов выбран, то составляющие его рёбра называются ветвями, а рёбра, введение которых приводит к образованию замкнутых контуров, называются хордами. Количество хорд определяется по формуле 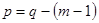 , где
, где 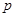 - количество хорд,
- количество хорд, 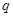 - количество рёбер,
- количество рёбер,  - количество вершин. Для приведенных выше остовов имеется по три хорды: (e1, e3, e7), (e2, e3, e7) и (e2, e4, e7), соответственно. Число хорд графа называется дефицитом графа иличислом Бетти. Число Бетти равно числу рёбер графа, которые надо удалить из него, чтобы получить дерево.
- количество вершин. Для приведенных выше остовов имеется по три хорды: (e1, e3, e7), (e2, e3, e7) и (e2, e4, e7), соответственно. Число хорд графа называется дефицитом графа иличислом Бетти. Число Бетти равно числу рёбер графа, которые надо удалить из него, чтобы получить дерево.
Многие важные задачи, возникающие, например, при изучении потоков в сетях (см. §7), приводят к понятию разреза. Перед тем, как дать его формальное определение, введем более общее понятие. Пусть Г=(V, Е) – связный граф и 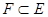 – некоторое подмножество его рёбер. При этом F называется разделяющим множеством тогда и только тогда, когда подграф Г'=(V, Е-F) несвязен. Здесь через Е-F обозначено множество ребер, которые принадлежат Е, но не принадлежат F. Разделяющие множества всегда существуют (если граф Г имеет, по крайней мере, две вершины), так как всегда можно положить F=E.
– некоторое подмножество его рёбер. При этом F называется разделяющим множеством тогда и только тогда, когда подграф Г'=(V, Е-F) несвязен. Здесь через Е-F обозначено множество ребер, которые принадлежат Е, но не принадлежат F. Разделяющие множества всегда существуют (если граф Г имеет, по крайней мере, две вершины), так как всегда можно положить F=E.
В общем случае, если задан связный граф Г=(V, Е),и множество его вершин разбито на два непустых подмножества W и W', то множество ребер, соединяющих W и W', называется разрезом. Для любого W это множество ребер будет непусто в силу связности графа Г, и следовательно, разрез определен.
Ориентированные графы
Граф называется ориентированным, или орграфом, если на каждом ребре задано направление, т. е. у каждого ребра фиксируются начало и конец. Направление ребра указывается стрелкой. Такие направленные ребра называются дугами. Цепью в орграфе называется такая последовательность дуг, в которой каждые две соседних дуги имеют общую вершину и никакая дуга не встречается более одного раза. Если направление цепи совпадает с направлением всех принадлежащих ей дуг, то цепь называется путем. В орграфах циклом называется путь, начало и конец которого совпадают.
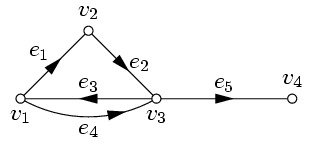
Рис. 3.
На рис. 3 дуги (e1, e4, e5) образуют цепь, а дуги (e1, e2, e5) – путь. Последовательность дуг (e1, e2, e3) составляет цикл, а последовательность (e1, e2, e4) не является циклом.
Каждая дуга считается положительно инцидентной для своей конечной вершины и отрицательно инцидентной для начальной. Число дуг, положительно инцидентных вершине v, называется положительной степенью vи обозначается δ+(v). Аналогично определяется отрицательная степень δ–(v). Например, на рис. 3 ребро e3 положительно инцидентно вершине v1,рёбра e1, e4 – отрицательно, следовательно, δ+(v)=1, δ–(v)=2.
При решении задач, связанных с графами, на компьютере, графическое задание орграфа оказывается неудобным. Вместо него используются так называемые матрицы инцидентности, которые определяются следующим образом. Пусть некоторый граф Г имеет m вершин v1… vmи n рёбер e1… en. Матрица инцидентности будет состоять из m строк и n столбцов, каждая строка соответствует вершине, столбец – ребру. Элемент aij, соответствующий вершине vi и ребру ej, равен +1, если вершина является начальной для ребра, -1 – если конечной, 2 – если и то и другое (т.е. если ej – петля в вершине vi), 0 –в остальных случаях. Таким образом, в каждом столбце имеется один или два отличных от нуля элемента. Например, для графа, изображенного на рис. 3, матрица инцидентности имеет вид:
| e1 | e2 | e3 | e4 | e5 | |||
| v1 | 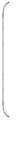 | -1 | 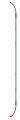 | ||||
| v2 | -1 | ||||||
| v3 | -1 | -1 | |||||
| v4 | -1 |
Матрицей инцидентности можно задавать и неориентированный граф, в этом случае для каждого ребра обеим концевым вершинам ставится в соответствие 1 , остальным – 0.
При использовании терминов «дерево», «лес», «разделяющее множество», «разрез» без специальной оговорки считается, что направления дуг не учитываются и рассматривается соответствующий неориентированный граф. Ориентированным деревом, растущим из корня v0 , называется ориентированный граф, если: (1) он образует дерево в неориентированном смысле, и (2) единственная цепь между v0 и любой другой вершиной w является путем из v0 в w. Очевидно, что любое дерево может иметь не более одного корня, и, вообще говоря, деревья орграфа могут быть неориентированными.
Аналогичным образом вводится понятие ориентированного покрывающего дерева. Например, для графа на рис. 3 единственное ориентированное покрывающее дерево имеет следующий вид:
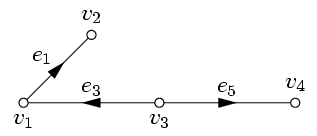 | (корнем является вершина v3 ) |
Сетью называется связный ориентированный граф G без петель, каждой дуге ej которого поставлено в соответствие некоторое число 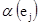 (или несколько чисел), т.е. на множестве ребер орграфа задана некоторая числовая функция
(или несколько чисел), т.е. на множестве ребер орграфа задана некоторая числовая функция 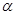 , которая обычно считается неотрицательной. Число
, которая обычно считается неотрицательной. Число 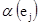 в зависимости от контекста называется либо длиной, либо весом, либо пропускной способностью дуги. При изображении сети
в зависимости от контекста называется либо длиной, либо весом, либо пропускной способностью дуги. При изображении сети 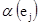 проставляется рядом с дугой ej. Подробно сети будут рассматриваться ниже в §7.
проставляется рядом с дугой ej. Подробно сети будут рассматриваться ниже в §7.
Уравнения и графы
Рассмотрим систему, состоящую из нескольких узлов, каждому из которых соответствует некоторый узловой сигнал (воздействие) 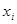 . Узлы связаны направленными линиями, по которым они могут принимать или передавать сигналы другим узлам. Каждая линия характеризуется величиной, которая называется передачей,иопределяется как отношение сигнала на выходе линии к сигналу на ее входе. Узел называется зависимым, если имеет одну или несколько входящих линий. Узловой сигнал предполагается равным сумме входных сигналов. Наличие выходящихлиний из узла
. Узлы связаны направленными линиями, по которым они могут принимать или передавать сигналы другим узлам. Каждая линия характеризуется величиной, которая называется передачей,иопределяется как отношение сигнала на выходе линии к сигналу на ее входе. Узел называется зависимым, если имеет одну или несколько входящих линий. Узловой сигнал предполагается равным сумме входных сигналов. Наличие выходящихлиний из узла 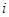 не влияет на сигнал этого узла
не влияет на сигнал этого узла 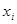 (они влияют на сигналы других узлов).
(они влияют на сигналы других узлов).
Такую систему можно представить в виде некоторого орграфа (сети), в котором узлам системы соответствуют вершины, линиям связи – дуги, направление которых соответствует направлению передачи сигнала. Вершины удобно обозначать их узловыми сигналами 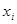 , дуги – парами чисел
, дуги – парами чисел 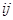 , где
, где 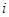 – номер узла, из которого выходит данная линия,
– номер узла, из которого выходит данная линия, 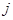 – в который входит. Передача дуги
– в который входит. Передача дуги 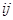 обозначается
обозначается 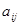 . Например:
. Например:
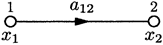
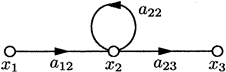
Первому из этих орграфов соответствует простейшее уравнение 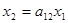 , второму – система уравнений
, второму – система уравнений 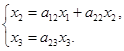
Рассмотрим систему трех уравнений: 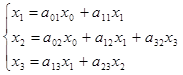
Ее граф имеет вид:
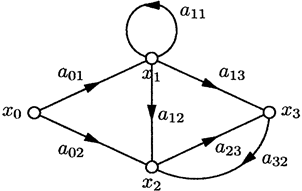
Здесь два контура обратной связи: петля 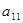 и цикл (
и цикл ( 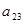 ,
, 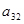 ).
).
Существует три типа вершин:
1) источники – вершины, которые имеют только выходящие дуги;
2) простые каскадные узлы – имеют как выходящие, так и входящие дуги;
3) стоки – вершины, имеющие только входящие дуги.
Источники соответствуют независимым переменным, а стоки - зависимым. Графы, не содержащие контуров обратной связи, называются каскадными графами.
Например, рассмотрим граф, показанный на рис. 4:
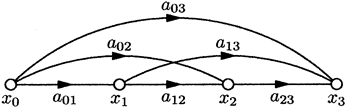 Рис. 4. Рис. 4. | 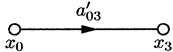 Рис. 5. Рис. 5. |
Он выражает следующие уравнения: 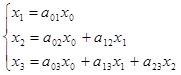 .
.
Так как имеются лишь один источник и один сток, которые связаны только прямыми путями (т.е. такими, вдоль которых номера вершин возрастают), то можно построить простой граф, задающий 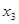 как функцию
как функцию  . Такой упрощенный граф (см. рис. 5) называется приведенным относительно исходного графа.
. Такой упрощенный граф (см. рис. 5) называется приведенным относительно исходного графа.
Искомую передачу легко определить, выразив в уравнениях 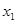 и
и  через
через  :
: 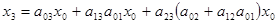 , откуда
, откуда 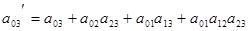 .
.
§5. Правила упрощения орграфов
для систем уравнений
Исключению зависимых переменных из системы уравнений соответствуют преобразования орграфов, позволяющие заменить последовательные и параллельные пути отдельными ветвями и, таким образом, упростить орграф.
Рассмотрим основные правила упрощения орграфов.
1. Передача последовательно соединенных рёбер равна произведению передач этих рёбер (рис.6). Действительно, 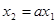 ,
, 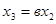 , откуда
, откуда 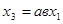 .
.
2. Передача двух параллельных одинаково направленных рёбер равна сумме передач этих рёбер (рис.7).
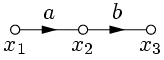 | => | 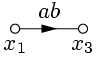 | 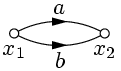 | => | 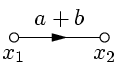 |
| Рис. 6. | Рис. 7. |
3. Устранение простой вершины(не входящей в контур обратной связи).
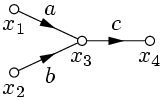 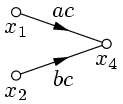 | 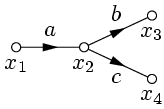 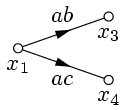 |
| Рис. 8. | Рис. 9. |
Действительно, 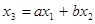 ,
, 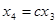 , откуда
, откуда 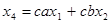 (рис. 8). Аналогично, для рис. 9, находим:
(рис. 8). Аналогично, для рис. 9, находим: 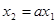 ,
, 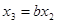 ,
, 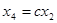 , откуда
, откуда 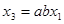 ,
, 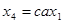 .
.
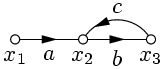
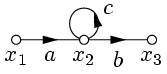
4. Устранение контура на пути (рис. 10).
Имеем: 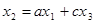 ,
, 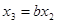 , следовательно,
, следовательно, 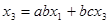 .
.
 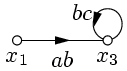 |  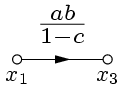 |
| Рис. 10. | Рис. 11. |
5. Исключение петли, когда к узлу подходит и из него отходит по одной ветви (рис. 11).
Очевидно, 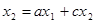 ,
, 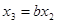 . Из первого равенства
. Из первого равенства 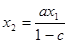 , тогда
, тогда 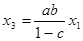 (предполагается, что
(предполагается, что 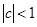 ).
).
6. Исключение петли, когда к узлу подходят и из него выходят несколько рёбер.
В этом случае вводится дополнительная вершина, к которому подходят те же ветви, которые подходили к узлу с петлей.
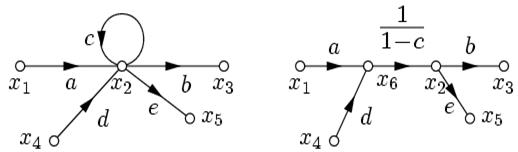
Для первого графа: 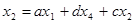 или
или 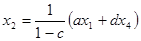 , откуда
, откуда
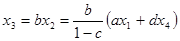 и
и 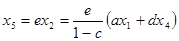 . Для второго графа:
. Для второго графа: 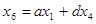 ,
, 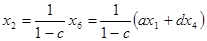 ,
, 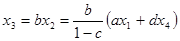 и
и
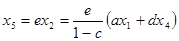 . Таким образом, при исключении петли передачи всех входящих рёбер умножаются на
. Таким образом, при исключении петли передачи всех входящих рёбер умножаются на 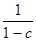 , а исходящие ветви остаются без изменения.
, а исходящие ветви остаются без изменения.
7. Замена двух и большего числа петель одной петлей.
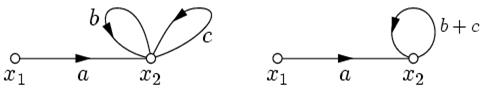
8. Удлинение (растяжение) вершину.
В некоторых случаях при преобразованиях графов оказывается полезным «удлинить» вершину. Пусть, например, надо удлинить вершину 2 графа, приведенного на рис. 12:
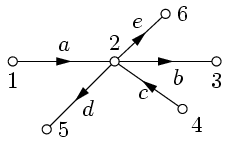 | 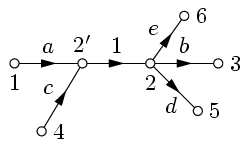 |
| Рис. 12. | Рис. 13. |
Для этого:
1) вершину 2 подразделяют на две: на старую вершину 2, от которой отходят те же ветви, что и в первоначальном графе, и на новую вершину 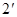 , к которому подходят те же ветви, что подходили к вершине 2 в исходном графе;
, к которому подходят те же ветви, что подходили к вершине 2 в исходном графе;
2) узлы 2 и 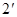 соединяют ребром, передача которого равна 1.
соединяют ребром, передача которого равна 1.
В результате получим граф, изображенный на рис. 13. Справедливость преобразования проверить самостоятельно.
9. Инверсия пути.
Рассмотрим уравнение: 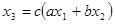 . Соответствующий ему граф показан на рис. 14. Здесь
. Соответствующий ему граф показан на рис. 14. Здесь 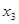 – зависимая переменная. Можно разрешить это уравнение относительно переменной
– зависимая переменная. Можно разрешить это уравнение относительно переменной 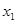 или
или  . Например,
. Например, 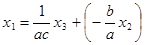 . Ему соответствует граф (см. рис. 15), в котором осуществлена инверсия пути по сравнению с исходным графом.
. Ему соответствует граф (см. рис. 15), в котором осуществлена инверсия пути по сравнению с исходным графом.
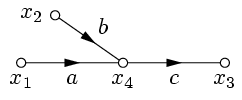 | 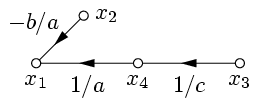 |
| Рис. 14. | Рис. 15. |
Рассмотрим несколько примеров.
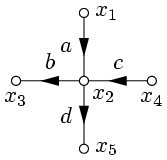
Пример 1. Построить граф по заданной системе уравнений 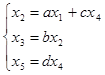 ; исключить вершину
; исключить вершину  и написать соответствующую систему уравнений.
и написать соответствующую систему уравнений.
Данной системе уравнений соответствует граф, показанный на рис. 16.
 |  |
| Рис. 16. | Рис. 17. |
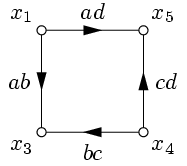
После исключения узла  получим граф, изображенный на рис. 17. Ему соответствует система уравнений
получим граф, изображенный на рис. 17. Ему соответствует система уравнений 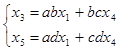 .
.
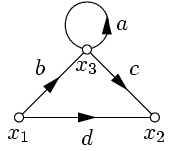
Пример 2. Исключить петлю и упростить граф, изображенный на рис. 18.
 | 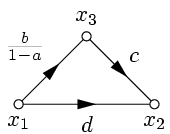 |
| Рис. 18. | Рис. 19. |
Сначала исключим петлю, применив правило 5 (рис. 19). Затем, в соответствии с правилом 1, исключим x3 (рис. 20) и применим правило 2 (рис. 21).
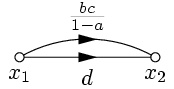 | 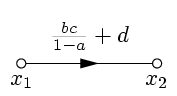 |
| Рис. 20. | Рис. 21. |
Таким образом, 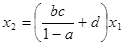 .
.
Пример 3. Исключить петлю и упростить граф, изображенный на рисунке:
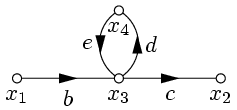
Применим правило 1 (рис. 22), затем правила 5 и 1 (рис. 23).
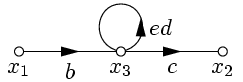 | 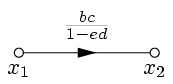 |
| Рис. 22. | Рис. 23. |
Таким образом, 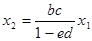 .
.
Пример 4. Упростить граф, изображенный на рисунке:
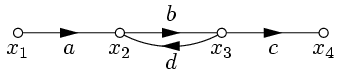
| Первый способ: | Второй способ: | ||
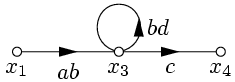 | 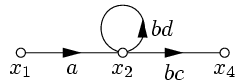 | ||
| Окончательно получим: | 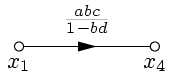 | 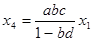 . . | |
Пример 5. Упростить граф, изображенный на рисунке:

Последовательные преобразования графа показаны на рис. 24 – рис. 26.
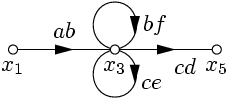 | 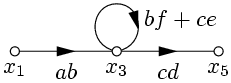 |
| Рис. 24. | Рис. 25. |
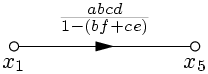 | 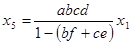 . . |
| Рис. 26. |
Пример 6. Дана система уравнений 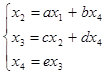 . Построить ее полный граф и упрощенный граф, в котором переменная
. Построить ее полный граф и упрощенный граф, в котором переменная 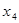 выражена через
выражена через 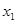 .
.
Полный граф системы показан на рис. 27. Преобразовав его, получим упрощенный граф (рис. 28).
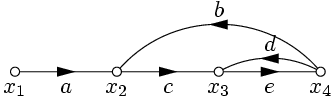 | 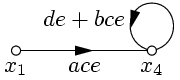 |
| Рис. 27. | Рис. 28. |
Таким образом, 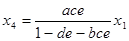 .
.
