Операция произведения двух матриц

Умножение матрицы 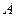размера 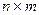на матрицу размера – операция, в результате которой получается матрица размера , каждый элемент которой равен сумме произведений элементов 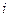-й строки матрицы 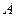на соответствующие элементы 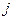-го столбца матрицы .

Рассмотрим матрицы

,

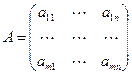здесь число столбцов матрицы равно числу строк матрицы .

, , .

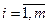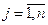Пример 3.

.

Замечание. Операцию умножения можно распространить на матриц , , …, размерности , , … , соответственно. В результате получится матрица размерности .

Пример 4.а) Фирма занимается реализацией четырёх видов товаров в трёх районах. Матрица уровня продаж имеет вид:

(объёмы продаж даны в тысячах штук). Цены (в тыс. руб/тыс. штук) заданы матрицей

.

Тогда для нахождения объёма продаж нужно найти произведение матриц :

б) , .

.

Свойства операции

1. (произведение матриц некоммутативно).

Если , то матрицы называются коммутирующими.

2. .

3. .

4. .

5. .

6. .

Предполагается, что все эти произведения существуют.

Операция транспонирования матрицы.

Транспонирование матрицы – операция, в результате которой строки и столбцы матрицы меняются местами. Обозначение .

, .

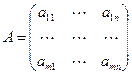Пример 5. , тогда .

Свойства операции транспонирования

1. .

2. .

3. .

4. .

5.Если для квадратной матрицы , то матрица называется симметрической, для неё .

Доказательство свойства 2

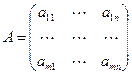размера ,

размера .

Тогда

Следовательно, .

Лекция 2

3. Понятие инверсии. Определитель матрицы n-го порядка.

Миноры, алгебраические дополнения элементов матрицы, определителя. Теорема Лапласа о разложении определителя по строке (столбцу).

3. Понятие инверсии. Определитель матрицы n-го порядка

Каждой квадратной матрице соответствует некоторое число, вычисляемое по определённым правилам. Это число называется определителем и обозначается . Рассмотрим правила вычисления определителей для частных случаев.

1. .

. (1.2)

Пример 1.

.

2. .

(1.3)

Вычисление определителя 3-го порядка по формуле (1.3) называется правилом треугольников. Схематично это правило можно изобразить следующим образом.

Элементы определителя изображены точками, линиями соединены те из них, которые нужно перемножить; «+» означает, что знак данных произведений не меняется, а «-» означает, что у произведения нужно поменять знак.

Пример 2.

Теперь рассмотрим общее правило вычисления определителя 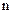-го порядка. Нам потребуются некоторые вспомогательные сведения.

Пусть имеется множество из 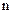элементов.

Определение 1. Множество называется упорядоченным, если каждому элементу данного множества поставлено в соответствие натуральное число от 1 до ( – число элементов множества), причем разным элементам ставятся в соответствие разные числа.

Упорядоченные множества отличаются либо числом элементов, либо порядком элементов.

Определение 2. Упорядоченные множества, составленные из элементов данного множества, отличающиеся лишь порядком элементов, называются перестановками.

Число всех перестановок из элементов обозначается и вычисляется по формуле

. (1.4)

Заметим, что ,

.

Определение 3. Инверсией в перестановке называется тот факт, когда большее число стоит впереди меньшего.

Вернёмся к определителю 3-го порядка. Он равен сумме шести слагаемых, каждое из которых является произведением трёх элементов, причем эти произведения содержат элементы каждой строки и каждого столбца, т.е. имеют вид , где – это числа 1,2,3, расставленные в определённом порядке. Это перестановки 123, 132, 213,231, 312,321, их .

Некоторые произведения входят в сумму со знаком «+», некоторые – со знаком «-». Как выбирается знак?

Со знаком «+» – произведения, у которых вторые индексы элементов образуют перестановки 123,231,312. Каждая из этих перестановок содержит четное число инверсий.

Со знаком «-» – те произведения, у которых вторые индексы элементов образуют перестановки 321, 213, 132. Они содержат нечетное число инверсий.

Таким образом, приходим к следующему правилу вычисления определителя 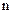- го порядка. Он равен алгебраической сумме произведений, содержащих по одному элементу из каждой строки и из каждого столбца. Произведение берётся со знаком «+», если вторые индексы элементов образуют перестановку с четным числом инверсий, со знаком «-», если с нечетным числом инверсий. При этом первые индексы элементов записаны в порядке возрастания.

, (1.5)

где – число инверсий данной перестановки.

Так как перестановок , то для вычислять определитель по этому правилу сложно.