Задания к лабораторной работе № 1
Задание 1.1.
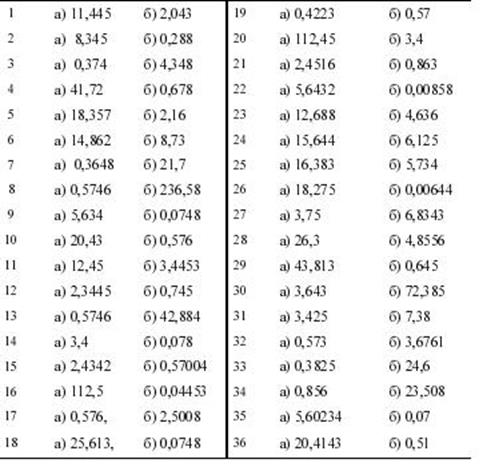
Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры (табл. 1.3):
а) в строгом смысле; б) в широком смысле.
Таблица 1.3. Варианты заданий для выполнения самостоятельной
работы
Задание 1.2.
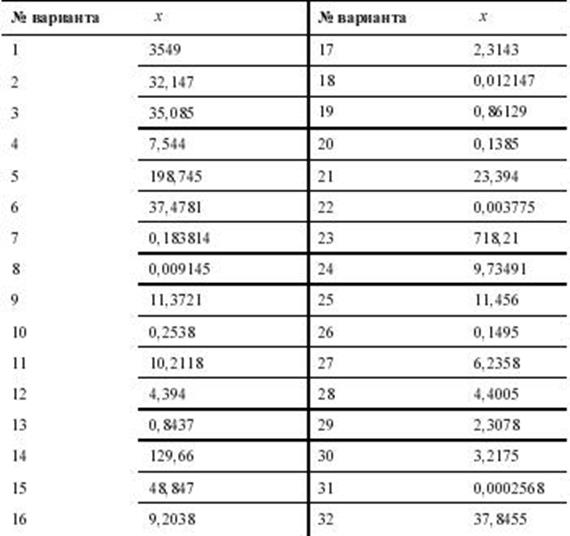
Число х (табл. 1.4.), все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата х1 ≈ х вычислить границы абсолютной и относительной погрешностей. В записи числа х1 указать количество верных цифр по абсолютной и относительной погрешностям
Таблица 1.4. Варианты заданий для выполнения самостоятельной
работы
Задание 1.3.
Вычислить значение величины z (табл. 1.5) при заданных значениях чисел a, b и c,используя систематический учет абсолютных погрешностей после каждой операции, а также с помощью метода границ. Найти абсолютную и относительную погрешности z и определить по ним количество верных цифр в z, если цифры a, и b с верны в строгом смысле.
Таблица 1.5. Варианты заданий для выполнения самостоятельной
работы
| № | Задание | Исходные данные | № | Задание | Исходные данные |
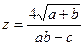 | a = 0,317 b = 3,27 c = 4,7561 | 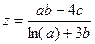 | a = 12,72 b = 0,34 c =0,0290 | ||
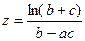 | a = 0,0399 b = 4,83 c =0,0721 | 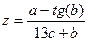 | a = 3,49 b = 0,845 c = 0,0037 | ||
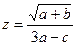 | a = 1,0574 b = 1,40 c = 1,1236 | 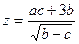 | a = 0,0976 b = 2,371 c = 1,15887 | ||
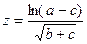 | a = 82,3574 b = 34,12 c = 7,00493 | 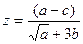 | a = 11,7 b = 0,0937 c = 5,081 | ||
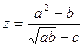 | a = 3,71452 b = 3,03 c = 0,756 | z = 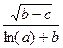 | a = 18,035 b = 3,7251 c = 0,071 | ||
z = 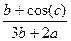 | a = 0,11587 b = 4,256 c = 3,00971 | z = 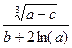 | a = 5,7568 b = 21,7 c = 2,65 | ||
z = 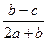 | a = 4,05 b = 6,723 c = 0,03254 | z = 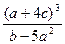 | a = 5,33 b = 23,123 c = 8,802 | ||
z = 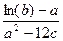 | a = 0,7219 b = 135,347 c = 0,013 | z = 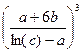 | a = 6,0031 b = 1,005 c = 1,6135 | ||
z = 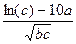 | a = 0,113 b = 0,1056 c = 89,4 | z = 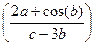 | a = 0,037 b = 5,777 c = 3,441 | ||
z = 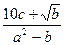 | a = 1,247 b = 0,346 c = 0,051 | z = = 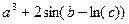 | a = 8,317 b = 13,521 c =6,123 | ||
z = 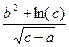 | a = 0,038 b = 3, 9353 c = 5,75 | z = 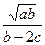 | a = 5,387 b = 13,527 c = 0,7565 | ||
z = 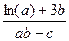 | a = 7,345 b = 0,31 c = 0,09871 | z = 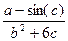 | a = 1,75 b = 1,215 c = 0,041 | ||
z = 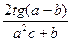 | a = 0,2471 b = 0,0948 c = 4,378 | z = 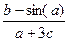 | a = 3,672 b = 4,63 c = 0,0278 | ||
z = 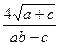 | a = 1,284 b = 4,009 c = 3,2175 | z = 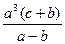 | a = 13,57 b = 3,7 c = 4,226 | ||
z = 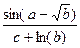 | a = 18,407 b = 149,12 c = 2,3078 | z = 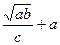 | a = 0,317 b = 13,57 c = 0,751 | ||
z = 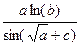 | a = 29,49 b = 87,878 c = 4,403 | z = 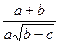 | a = 0,317 b = 33,827 c = 14,85 | ||
z = 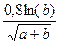 | a = 74,079 b = 5,3091 c = 6,234 | z = 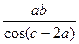 | a = 5,52 b = 3,27 c = 14,123 | ||
z = 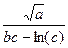 | a = 3,4 b = 6,22 c = 0,149 | z = 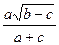 | a = 9,542 b = 3,128 c = 0,17 | ||
z = 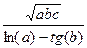 | a = 9,79 b = 2,3327 c = 4,198 | z = 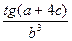 | a = 5,147 b = 6,222 c = 0,0075 | ||
z = 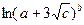 | a = 6,66 b = 3,5 c = 1,141 | z = 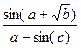 | a = 2,258 b = 0,027 c = 9,87 |
Задание 1.4.
Решить следующие задачи, используя метод границ.
1. Длина воздушной трассы между двумя пунктами равна S км. Самолет преодолевает это расстояние за время t ч. Определить границы средней скорости самолета, если 4950 ≤ S ≤ 5050; 5,9 ≤ t ≤ 6,1.
2. Электроплитка рассчитана на напряжение 220 ± 10 В. Найти сопротивление спирали электроплитки, если известно, что через нее должен пройти ток 5 ± 0,1 А.
3. Медный брусок имеет объем V м3 (0,0064 ≤ V ≤ 0,0065). Найти его массу, если плотность меди γ кг/м3 составляет 8899 ≤ γ ≤ 8901.
Задание 1.5.
Решить следующие задачи, используя общую формулу погрешности.
1. Удельное электрическое сопротивление ρ металла круглого провода длиной l м с поперечным сечением d мм и сопротивлением R Ом определяется по формуле ρ =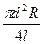 
. Найти ρ, если: l = 12,50 ± 0,01 м, d = 2,00 ± 0,01 мм. R = 0,068 ± 0,0005 Ом, π = 3,141 ± 0,001. Определить относительную погрешность ρ.
2. Вертикальный цилиндрический резервуар наполнен жидкостью. Определить время, необходимое для опорожнения резервуара через круглое отверстие в дне. Диаметр резервуара D = 1 ± 0,01 м, высота уровня жидкости Н = 2± 0,02 м, диаметр отверстия дна d = 0.03 ± 0,001 м, коэффициент расхода μ=0,61± 0,02. Расчет (в секундах) ведется по формуле
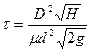
Лабораторная работа №2