III. Подбор сечения балки
Условие прочности для балок с сечениями, симметричными относительно нейтральной оси, имеет вид:
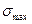 =
= 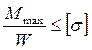 ,
,
где W – осевой момент сопротивления сечения.
Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимую величину осевого момента сопротивления:
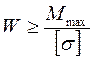 .
.
Исходя из формы поперечного сечения, по найденному моменту его сопротивления находят размеры сечения.
Требуется:
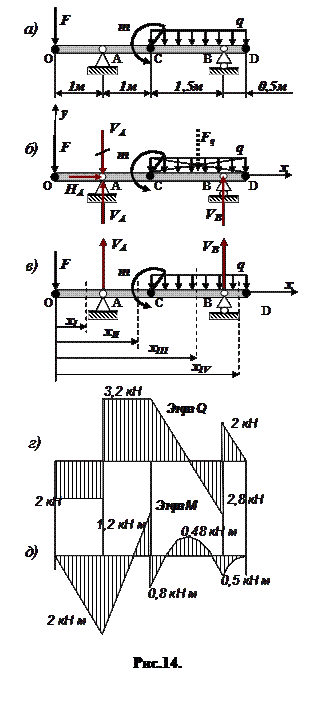
Выполнить расчет балки на двух опорах, изображенной на рис.14.а. Для этого необходимо решить следующие задачи:
a. Построить эпюры поперечных сил Q и изгибающих моментов М.
b. Из расчета на прочность подобрать сечение балки из пластичного материала следующих профилей:
- - в форме сплошного круга,
- - в форме прямоугольника с соотношением сторон 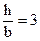 .
.
При расчетах принять: 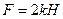 ,
, 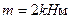 ,
, 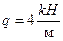 ,
, 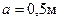 ,
, 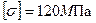 .
.
Решение:
Расчет выполняется в полном соответствии с п.3.4.1
I. Определение опорных реакций (рис.14.б)
Вначале освободим балку от опор, изобразив все действующие на нее нагрузки, включая неизвестные (направления векторов последних выберем произвольно). Вектор 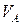 -вниз,
-вниз, 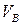 – вверх.
– вверх.
Назначаем систему координат, связанную с левым концом балки. Ось Х направляем вдоль оси балки вправо. Ось Y – вертикальна. Ввиду отсутствия внешней нагрузки, имеющей горизонтальную составляющую, из уравнения статического равновесия проекций всех нагрузок на ось Х можно сразу установить, что
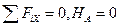 .
.
При составлении уравнений статического равновесия моментов примем для удобства правило знаков, по которому сила или сосредоточенный момент, поворачивающие балку вокруг данной точки в направлении вращения часовой стрелки, обуславливают положительное слагаемое в данном уравнении моментов.
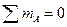 ,
, 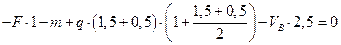 ,
,
откуда 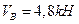 .
.
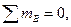
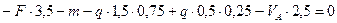 ,
,
откуда 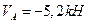 .
.
Обратим внимание на знаки вычисленных реакций 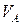 и
и 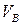 . В случае с
. В случае с 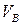 назначенное направление этого вектора оказалось удачным, об этом свидетельствует положительное значение
назначенное направление этого вектора оказалось удачным, об этом свидетельствует положительное значение 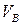 .Реакция
.Реакция 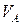 получила отрицательное значение, что означает необходимость изменить направление этого вектора на противоположное, т.е. направить его вверх. Прежний вектор
получила отрицательное значение, что означает необходимость изменить направление этого вектора на противоположное, т.е. направить его вверх. Прежний вектор 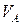 пометим короткой наклонной чертой, в дальнейших расчетах он не используется.
пометим короткой наклонной чертой, в дальнейших расчетах он не используется.
Проверку осуществим на основе уравнения 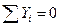
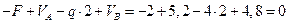 .
.
Следовательно, опорные реакции определены верно.
Разделим балку на участки:
I участок 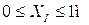 II участок
II участок 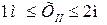
III участок 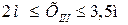 IV участок
IV участок 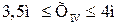 .
.
Для дальнейших расчетов представляем расчетную схему балки согласно рис.15.в.
II.Построение эпюр поперечных сил (рис.14.г)
На участке I величину и знак Q определим, проведя на нем произвольное сечение и рассматривая равновесие левой отсеченной части (отдельно ее не показываем). Внешней нагрузкой, действующей на левую отсеченную часть балки, является сила 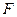 , стремящаяся повернуть эту часть против хода часовой стрелки. Следовательно, здесь Q отрицательна.
, стремящаяся повернуть эту часть против хода часовой стрелки. Следовательно, здесь Q отрицательна.
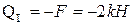 .
.
На этом участке эпюра Q – прямая, параллельная оси абсцисс.
На участке II поперечная сила также постоянна. На левую отсеченную часть действуют силы F и 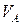 .
.
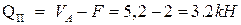
Отметим, что в сечении балки над левой опорой А на эпюре Q получается скачок на величину силы VA.
На участке III действует распределенная нагрузка, поэтому поперечная сила Q будет изменяться по линейному закону в виде наклонной прямой в зависимости от значения текущей координаты 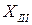 . Сечение балки в точке С, где начинает действовать распределенная нагрузка, сдвинуто вправо от точки О начала координат на 2м. По этой причине выражение для Q выглядит следующим образом:
. Сечение балки в точке С, где начинает действовать распределенная нагрузка, сдвинуто вправо от точки О начала координат на 2м. По этой причине выражение для Q выглядит следующим образом:
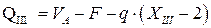 .
.
 Произведение
Произведение 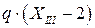 представляет собой выражение для внешней силы от распределенной нагрузки.
представляет собой выражение для внешней силы от распределенной нагрузки.
Подставляя крайние значения 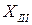 получаем величины Q в точках С и В.
получаем величины Q в точках С и В.
При 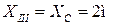
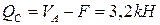 .
.
При 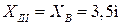
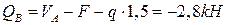 .
.
Поскольку на этом участке наблюдается изменение знака Q, то найдем координату 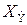 , при которой поперечная сила становится равной нулю. С этой целью решаем уравнение
, при которой поперечная сила становится равной нулю. С этой целью решаем уравнение
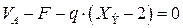 .
.
Получаем 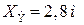 .
.
Выражение для QIV на последнем участке отличается от QIII на величину 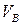
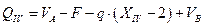 .
.
При 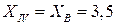 м
м 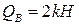 .
.
При 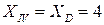 мQD = 0.
мQD = 0.
Полученные значения поперечной силы наносим на эпюру Q, соединяя прямыми линиями значения Q на краях каждого участка.
III.Построение эпюр изгибающих моментов (рис.14.д)
На участке I изгибающий момент изменяется по линейному закону.
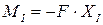 .
.
Знак минус перед силой F поставлен по той причине, что левая часть балки на этом участке от силы F изгибается выпуклостью вверх, т.е. сжатые волокна балки находятся снизу.
При 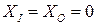
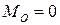 ,
,
при 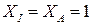 м
м 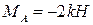 м.
м.
На участке II эпюра момента также имеет линейный вид:
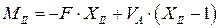 .
.
Здесь сила VA приложена к балке снизу, поэтому от нее балка изгибается выпуклостью вниз, т.е. сжатые волокна расположены сверху. Плечо момента от силы VA до рассматриваемого сечения с координатой 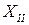 равно
равно 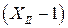 , т.к. оно короче плеча до силы F на 1м.
, т.к. оно короче плеча до силы F на 1м.
Подставляем крайние значения текущей координаты.
При 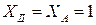 м
м 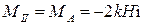 ,
,
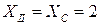 м
м 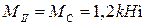 .
.
На участке III для сечения с координатой 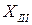 начинает действовать распределенная нагрузка, что является причиной для изменения характера эпюры момента; она становится квадратичной параболой.
начинает действовать распределенная нагрузка, что является причиной для изменения характера эпюры момента; она становится квадратичной параболой.
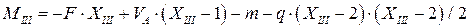 .
.
В этом выражении составляющая изгибающего момента от распределенной нагрузки имеет 3 сомножителя. Второй сомножитель 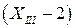 является расстоянием от сечения с координатой
является расстоянием от сечения с координатой 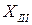 до сечения, где начинает действовать распределенная нагрузка, т.е. до точки
до сечения, где начинает действовать распределенная нагрузка, т.е. до точки 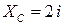 . Суммарное воздействие на балку от распределенной нагрузки, равное
. Суммарное воздействие на балку от распределенной нагрузки, равное 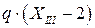 , эквивалентно сосредоточенной нагрузке того же значения, но приложенной точно посередине этого участка. По этой причине плечо эквивалента распределенной нагрузки до рассматриваемого сечения всегда вдвое короче длины нагруженного распределенной нагрузкой участка, а именно:
, эквивалентно сосредоточенной нагрузке того же значения, но приложенной точно посередине этого участка. По этой причине плечо эквивалента распределенной нагрузки до рассматриваемого сечения всегда вдвое короче длины нагруженного распределенной нагрузкой участка, а именно: 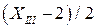 .
.
Следует обратить внимание, что в точке С приложен сосредоточенный момент, что вызывает соответствующий скачок изгибающего момента на эпюре. Сосредоточенный момент берется со знаком минус, т.к. он гнет левую часть балки выпуклостью вверх (сжатые волокна снизу).
При 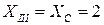 м
м 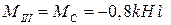 ,
,
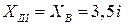
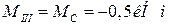 .
.
Найдем вершину квадратичной параболы, т.е. экстремальное значение изгибающего момента в той координате 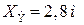 , которой соответствует нулевое значение QIII.
, которой соответствует нулевое значение QIII.
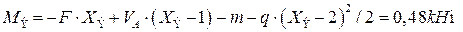 .
.
Для IV участка изгибающий момент имеет следующий вид
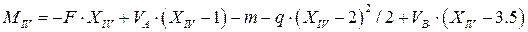 .
.
По крайним значениям строим эпюру, которая также имеет вид квадратичной параболы, выпуклой частью обращенной навстречу распределенной нагрузке.
При 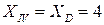 м
м 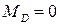 .
.
