Наивная и аксиоматическая теория множеств аксиома выбора и гипотеза континуума
Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным «множеством». Например, натуральное число, по Кантору, следовало рассматривать как множество, состоящее из единственного элемента другого множества, называемого «натуральным рядом» — который, в свою очередь, сам представляет собой множество, При этом общему понятию «множества», рассматривавшемуся им в качестве центрального для математики, Кантор давал мало что определяющие определения вроде «множество есть многое, мыслимое как единое», и т. Д. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» могут существенно зависеть от выбора аксиоматики. Аксио́ма вы́бора утверждает: «Для каждого семейства 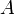 непустых непересекающихся множествсуществует множество
непустых непересекающихся множествсуществует множество 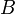 , имеющее один и только один общий элемент с каждым из множеств
, имеющее один и только один общий элемент с каждым из множеств 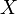 , принадлежащих
, принадлежащих 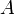 ». В 1877 году Георг Кантор выдвинул и впоследствии безуспешно пытался доказать так называемуюконти́нуум-гипо́тезу, оказалась гипотеза континуума, которая состоит в том, что между множеством натуральных чисел и множеством всех вещественных чисел, как между двумя мощностями, нет других мощностей. Оказалось, что эта гипотеза может быть принята или в таком виде (т. е. таких множеств нет) или в виде отрицания ее (т. е. такие множества есть), от этого не меняется система основных аксиом теории множеств'. Т. е. эта гипотеза - то самое утверждение, которое обещала теорема Геделя о неполноте любой аксиоматической теории.
». В 1877 году Георг Кантор выдвинул и впоследствии безуспешно пытался доказать так называемуюконти́нуум-гипо́тезу, оказалась гипотеза континуума, которая состоит в том, что между множеством натуральных чисел и множеством всех вещественных чисел, как между двумя мощностями, нет других мощностей. Оказалось, что эта гипотеза может быть принята или в таком виде (т. е. таких множеств нет) или в виде отрицания ее (т. е. такие множества есть), от этого не меняется система основных аксиом теории множеств'. Т. е. эта гипотеза - то самое утверждение, которое обещала теорема Геделя о неполноте любой аксиоматической теории.
13. конструктивная математика и проблемы построения анализа
Конструктивная математика, абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и о их результатах — конструктивных объектах. Абстрактность К. м. проявляется прежде всего в том, что в ней систематически применяются две абстракции: абстракция потенциальной осуществимости и абстракция отождествления. Абстракцию потенциальной осуществимости используют, когда отвлекаются от практических ограничений конструктивных возможностей в пространстве, времени и материале. Абстракцию отождествления используют, когда говорят о двух в том или ином смысле одинаковых объектах как об одном и том же объекте. В К. м. не применяется характерная для теоретико-множественной математики абстракция актуальной бесконечности, связанная с рассмотрением никогда не завершаемых процессов как бесконечно продолженных и тем самым как бы завершенных.
