Коэффициент перекрытия
На рис. 5.15 изображена пара взаимодействующих зубьев в двух положениях – в момент начала их участия в зацеплении в точке  и в момент окончания – в точке
и в момент окончания – в точке  .
.
С момента входа какого-либо зуба в зацепление до момента выхода из него каждое из колес пары повернется на так называемый угол перекрытия  и
и  . Если каждый из этих углов равен угловому шагу соответствующего колеса, т.е.
. Если каждый из этих углов равен угловому шагу соответствующего колеса, т.е.
 ,
,  , (5.47)
, (5.47)
 |
| Рис. 5.15 |
то каждая пара профилей входит в зацепление именно в тот момент, когда предыдущая пара (т.е. пара, ранее вступившая в контакт) выходит из зацепления.
Для того чтобы процесс зацепления пары колес был непрерывным, необходимо, очевидно, чтобы каждая новая пара профилей вступала в контакт до выхода из зацепления предыдущей пары; это возможно только при  .
.
Отношение  одинаково для обоих колес, его обозначают
одинаково для обоих колес, его обозначают  и называют торцовым коэффициентом перекрытия; поскольку углы поворота зацепляющихся эвольвентных колес пропорциональны перемещению контактной точки по линии зацепления, то
и называют торцовым коэффициентом перекрытия; поскольку углы поворота зацепляющихся эвольвентных колес пропорциональны перемещению контактной точки по линии зацепления, то
 . (5.48)
. (5.48)
Для прямозубых колес вместо обозначения  обычно используют символ e и в названии термина опускают слово «торцовый».
обычно используют символ e и в названии термина опускают слово «торцовый».
Можно показать, что для любого колеса пары
 , (5.49)
, (5.49)
с учетом (5.42), (5.44) и (5.47), коэффициент перекрытия
 . (5.50)
. (5.50)
Подытоживая сказанное, отметим, что коэффициент перекрытия характеризует непрерывность и плавность зацепления пары; теоретически работа передачи возможна при  , но на практике считают, что передача спроектирована верно, если для нее
, но на практике считают, что передача спроектирована верно, если для нее  .
.
Характерные точки активных профилей зубьев и линии зацепления
На рис. 5.16 показан активный профиль  колеса
колеса 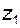 и соответствующая активная линия зацепления
и соответствующая активная линия зацепления  пары с коэффициентом перекрытия
пары с коэффициентом перекрытия  (т.е. при длине активной линии зацепления
(т.е. при длине активной линии зацепления  ).
).
 |
| Рис. 5.16 |
Если считать колесо 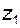 в этой паре ведущим, то на рисунке показан момент входа в зацепление изображенного зуба в точке
в этой паре ведущим, то на рисунке показан момент входа в зацепление изображенного зуба в точке  линии зацепления.
линии зацепления.
Поскольку расстояние по линии зацепления между соседними контактными точками равно основному шагу  , то при контактировании профилей на участке
, то при контактировании профилей на участке  другая (соседняя) пара профилей обязательно будет взаимодействовать на участке
другая (соседняя) пара профилей обязательно будет взаимодействовать на участке  линии зацепления. Следовательно, точки
линии зацепления. Следовательно, точки  и
и  (построение точек понятно из рисунка) выделяют на линии зацепления, и на сопряженных профилях так называемые зоны двупарной (
(построение точек понятно из рисунка) выделяют на линии зацепления, и на сопряженных профилях так называемые зоны двупарной (  и
и  – на рисунке выделены двойными линиями) и однопарной(
– на рисунке выделены двойными линиями) и однопарной(  ) работызубьев.
) работызубьев.
Отметим, что при однопарной работе зубьев их рабочие поверхности испытывают наибольшие контактные напряжения.
5.7. Последовательность проектирования
эвольвентной зубчатой передачи,
составленной из колес, нарезанных
стандартным реечным инструментом
Исходные данные
В практике проектирования зубчатых передач встречаются разные задачи и различные варианты сочетания исходных данных; ограничимся случаем, когда проектировщику заданы:
модуль m, мм;
числа зубьев колес 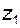 и
и 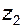 .
.
Кроме указанных параметров может оказаться заданным межосевое расстояние  (когда проектируемую передачу требуется по условиям компоновки агрегата вписать в заранее заданные габариты); возможен также случай, когда это расстояние не задано, но его требуется округлить, подчиняясь каким-либо правилам (до целого числа миллиметров, или выбрать его из ряда стандартных чисел и т.д.). Большинство приводимых ниже формул и выражений уже встречались ранее, здесь они приведены в строгую систему и расположены в требуемой последовательности.
(когда проектируемую передачу требуется по условиям компоновки агрегата вписать в заранее заданные габариты); возможен также случай, когда это расстояние не задано, но его требуется округлить, подчиняясь каким-либо правилам (до целого числа миллиметров, или выбрать его из ряда стандартных чисел и т.д.). Большинство приводимых ниже формул и выражений уже встречались ранее, здесь они приведены в строгую систему и расположены в требуемой последовательности.
Наиболее распространен случай, когда  не задано, но его необходимо на определенном этапе проектирования округлить.
не задано, но его необходимо на определенном этапе проектирования округлить.
Предлагается такой порядок действий:
выбор коэффициентов смещения  и
и  ; обычно здесь руководствуются рекомендациями, приведенными в литературе или каких-либо указаниях, учитывающими требования к проектируемой передаче.
; обычно здесь руководствуются рекомендациями, приведенными в литературе или каких-либо указаниях, учитывающими требования к проектируемой передаче.
При необходимости последующего округления  эти значения
эти значения  и
и  следует считать предварительными, подлежащими последующему уточнению.
следует считать предварительными, подлежащими последующему уточнению.
Далее рассчитываются следующие величины:
