Тема 1. «Множества. Числовые множества: комплексные числа»
Контрольная работа № 2 студентов группы 3ЭЭб -01-11зп
1. Рецензии преподавателя на контрольные работы позволяют студенту судить о степени усвоения им соответствующего раздела курса, указывают на имеющиеся у него пробелы и помогают сформулировать вопросы для постановки их перед преподавателем на консультации.
2. Следует приступать к выполнению контрольных заданий только после изучения теоретического материала и приобретения навыков решения соответствующих задач.
3. При подготовке к выполнению контрольной работы студент может использовать общие рекомендации по работе над курсом математики.
4. При выполнении контрольных работ нужно соблюдать следующие требования:
1) контрольная работа выполняется в тетради (Распечатать титульный лист, его см. на 2 стр, и приклеить на первый лист тетради);
2) у каждого студента свой номер варианта (в тексте задания фигурирует номер варианта):
| Номер варианта | Фамилия студента | Номер варианта | Фамилия студента |
| № 1 | Беляев Е.Н. | № 20 | Медников С.Е. |
| № 2 | Виноградов С.И. | № 21 | Морозов К.С. |
| № 3 | Волкова М.С. | № 22 | Мохов А.А. |
| № 4 | Воронов А.С. | № 23 | Носков А.И. |
| № 5 | Гончаренко М.В. | № 24 | Носов И.В. |
| № 6 | Денисов А.А. | № 25 | Орехов А.В. |
| № 7 | Долгодворов Н.А. | № 26 | Панифодов Е.С. |
| № 8 | Егоровцев А.В. | № 27 | Посланский А.А. |
| № 9 | Епишин М.М. | № 28 | Сергиенко С.В. |
| № 10 | Звонцев А.Д. | № 29 | Серебров С.Н. |
| № 11 | Ивашинин К.В. | № 30 | Мамутов Р.У. |
| № 12 | Калев С.А. | № 31 | Смирнов В.Е. |
| № 13 | Карлов Д.О. | № 32 | Соколов А.С. |
| № 14 | Келбусов В.А. | № 33 | Степакова А.А. |
| № 15 | Комлев А.А. | № 34 | Тарасов И.С. |
| № 16 | Копылов И.В. | № 35 | Ушков И.В. |
| № 17 | Кузнецов И.С. | № 36 | Хрынов А.Л. |
| № 18 | Кукауппи М.И. | № 37 | Цветков С.В. |
| № 19 | Куницин К.В. | № 38. | Юрковская Н.Н. |
3) задания выполняются строго по порядку, каждое задание – с новой страницы;
4) текст задачи переписывается в тетрадь, решение сопровождается краткими пояснениями;
5) чертежи выполняются с помощью линейки и карандаша;
6) работа над ошибками выполняется в той же тетради после заголовка «Работа над ошибками».
5. Контрольная работа сдается на кафедру математики и информатики (ауд. 403) до начала сессии. Преподавателю на проверку полагается две недели! К экзамену допускаются студенты, имеющие зачет по работе.
| МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» |
| Институт информационных технологий |
| наименование института (факультета) |
| кафедра математики и информатики |
| наименование кафедры |
| Контрольная работа № ___2_____ по дисциплине Высшая математика |
| наименование дисциплины в соответствие с учебным планом |
| студента (студентки) |
| фамилия, имя, отчество |
| Специальность: |
| Группа: 3ЭЭб -01-11зп |
| Вариант № ______ Шифр зачетной книжки ______________________ Проверил _____ Кашинцева О.А. ФИО преподавателя Оценка ________________________ Количество баллов _____________ Подпись _______________________ Дата ___________________________ |
Литература.
1. Задачник – практикум по математике. Пособие для студентов – заочников. Под редакцией проф. Н. Я. Виленкина. Москва, «Просвещение», 1977.
2. Данко, П.Е. Высшая математика в упражнениях и задачах. Часть 1. В.: 2 ч. [текст] / П.Е. Данко, А.Г. Попов, Т.А. Кожевникова. – М.: ОНИКС, 21 век. Мир и образование, 2008.–368 с.
3. Киселева Г.А. Математика. Методические указания по подготовке к контрольным работам. Часть 2. Часть 3. ГОУ ВПО Череповецкий государственный университет, 2010.
4. Гордобаева Т.В. Математика. Учебное пособие.
5. Лекции преподавателя.
Контрольная работа № 2.
Тема 1. «Множества. Числовые множества: комплексные числа».
Задание № 1. Найти множества(A È B)\(A Ç B), 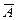 ,
, 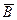 и изобразить их на диаграммах Эйлера-Венна.
и изобразить их на диаграммах Эйлера-Венна.
| Вариант | Множества А и В | Универсальное множество U |
| A = {x| x Î Z,– 2 ≤ x < 2}, B = {x| x = 2n – 3, n Î N, n ≤ 4} | U = {x| x Î Z, x Î [– 4, 7]} | |
| A = {x| x Î Z, – 3 ≤ x < 0}, B = {x| x = – 2n +1, n Î N, n ≤ 5} | U = {x| x Î Z, x Î [– 11, 0]} | |
| A = {x| x = 3n +1, n Î N, n < 5}, B = {x| x Î Z, 5 < x < 12} | U = {x| x Î Z, x Î [2, 14]} | |
| A = {x| x = n – 2, n Î N, n ≤ 5}, B = {x| x Î Z, – 2 ≤ x ≤ 1} | U = {x| x Î Z, x Î [– 4, 5]} | |
| A = {x| x = n + 3, n Î N, 3 ≤ n < 7}, B = {x| x Î Z, 5 ≤ x ≤ 8} | U = {x| x Î Z, x Î [2, 11]} | |
| A = {x| x Î Z, 3 ≤ x < 10}, B = {x| x = 2n+1, n Î N, n < 4} | U = {x| x Î Z, x Î [2, 17]} | |
| A = {x| x = 2n – 1, n Î N, 2 ≤ n ≤ 4}, B = {x| x Î Z, 4 < x ≤ 9} | U = {x| x Î Z, x Î [1, 10]} | |
| A = {x| x = 3n – 2, n Î N, n ≤ 3}, B = {x| x Î Z, 1 < x ≤ 4} | U = {x| x Î Z, x Î [0, 10]} | |
| A = {x| x = n – 4, n Î N, n ≤ 5}, B = {x| x Î Z, – 3 < x ≤ 3} | U = {x| x Î Z, x Î [– 4, 6]} | |
| A = {x| x =5n – 4, n Î N, n ≤ 3}, B = {x| x Î Z, 0 ≤ x ≤ 6} | U = {x| x Î Z, x Î [– 1, 12]} | |
| A = {x| x = n + 2, n Î N, n ≤ 5}, B = {x| x Î Z, – 1 ≤ x ≤ 3} | U = {x| x Î Z, x Î [– 4, 6]} | |
| A = {x| x =2 n + 2, n Î Z, -2 ≤ n ≤ 2}, B = {x| x Î N, x < 3} | U = {x| x Î Z, x Î [– 3, 7]} | |
| A = {x| x Î Z, 3 < x < 7}, B = {x| x = 2n+1, n Î N, n < 2} | U = {x| x Î Z, x Î [2, 10]} | |
| A = {x| x Î N x ≤ 9}, B = {x| x = n - 1, n Î N, x Î Z, n < 4} | U = {x| x Î Z, x Î [-2, 10]} | |
| A = {x| x Î Z,– 3 ≤ x < 2}, B = {x| x = 2n – 2, n Î N, n ≤ 4} | U = {x| x Î Z, x Î [– 4, 8]} | |
| A = {x| x Î Z, – 3 ≤ x < 1}, B = {x| x = – 2n -1, n Î N, n ≤ 5} | U = {x| x Î Z, x Î [– 12, 2]} | |
| A = {x| x = 3n +2, n Î N, n < 3}, B = {x| x Î Z, 5 < x < 10} | U = {x| x Î Z, x Î [2, 14]} | |
| A = {x| x = n 2, n Î N, n ≤ 3}, B = {x| x Î Z, – 2 ≤ x ≤ 3} | U = {x| x Î Z, x Î [– 4, 10]} | |
| A = {x| x = n – 5, n Î N, n ≤ 5}, B = {x| x Î Z, – 3 < x ≤ 5} | U = {x| x Î Z, x Î [– 5, 10]} | |
| A = {x| x =5n – 3, n Î N, n < 3}, B = {x| x Î Z, 0 ≤ x ≤ 5} | U = {x| x Î Z, x Î [– 1, 7]} | |
| A = {x| x Î Z, -3 ≤ x < 7}, B = {x| x = n2, n Î N, n < 3} | U = {x| x Î Z, x Î [-5, 15]} | |
| A = {x| x = 3n – 1, n Î N, 0 < n ≤ 2}, B = {x| x Î Z, -1 < x ≤ 4} | U = {x| x Î Z, x Î [-1, 10]} | |
| A = {x| x = n 2, n Î N, n < 3}, B = {x| x Î Z, – 1 ≤ x < 3} | U = {x| x Î Z, x Î [– 4, 9]} | |
| A = {x| x = n – 3, n Î N, n < 4}, B = {x| x Î Z, – 3 < x ≤ 3} | U = {x| x Î Z, x Î [– 5, 5]} | |
| A = {x| x =3n – 3, n Î N, n < 3}, B = {x| x Î Z, -1 ≤ x < 5} | U = {x| x Î Z, x Î [– 2, 7]} | |
| A = {x| x Î Z, -2 ≤ x < 5}, B = {x| x = n2, n Î N, n ≤ 3} | U = {x| x Î Z, x Î [-5, 15]} | |
| A = {x| x = 3n +1, n Î N, 0 < n ≤ 2}, B = {x| x Î Z, -1 < x ≤ 3} | U = {x| x Î Z, x Î [-1, 10]} | |
| A = {x| x Î Z,– 2 ≤ x < 3}, B = {x| x = 2n – 2, n Î N, n ≤ 4} | U = {x| x Î Z, x Î [– 4, 8]} | |
| A = {x| x Î Z, – 4 ≤ x < 0}, B = {x| x = – 2n +3, n Î N, n ≤ 4} | U = {x| x Î Z, x Î [– 8, 0]} | |
| A = {x| x = 3n +2, n Î N, n < 3}, B = {x| x Î Z, 5 < x < 10} | U = {x| x Î Z, x Î [2, 14]} | |
| A = {x| x = n – 2, n Î N, n ≤ 5}, B = {x| x Î Z, – 2 ≤ x ≤ 3} | U = {x| x Î Z, x Î [– 4, 6]} | |
| A = {x| x = n + 3, n Î N, 2 ≤ n < 7}, B = {x| x Î Z, 3 ≤ x ≤ 9} | U = {x| x Î Z, x Î [2, 11]} | |
| A = {x| x Î Z, 3 ≤ x < 9}, B = {x| x = 2n+1, n Î N, n < 3} | U = {x| x Î Z, x Î [2, 16]} | |
| A = {x| x = 2n – 1, n Î N, 2 ≤ n ≤ 4}, B = {x| x Î Z, 4 < x ≤ 6} | U = {x| x Î Z, x Î [1, 9]} | |
| A = {x| x = 3n – 1, n Î N, n ≤ 3}, B = {x| x Î Z, 1 < x ≤ 5} | U = {x| x Î Z, x Î [0, 10]} | |
| A = {x| x = n – 4, n Î N, n ≤ 3}, B = {x| x Î Z, – 3 < x ≤ 3} | U = {x| x Î Z, x Î [– 6, 6]} | |
| A = {x| x =5n – 3, n Î N, n ≤ 3}, B = {x| x Î Z, -1 ≤ x < 5} | U = {x| x Î Z, x Î [– 2, 12]} | |
| A = {x| x = n + 2, n Î N, n ≤ 4}, B = {x| x Î Z, – 1 < x ≤ 3} | U = {x| x Î Z, x Î [– 4, 7]} |
Задание № 2. Комплексные числа. (Значения косинусов и синусов находить в радианах (cos1 = 0,54, sin1 = 0,84). Ответ записать в виде десятичных чисел).
Вариант № 1.
1) Найти и изобразить геометрически на комплексной плоскости число 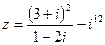 . 2) Найти сумму и частное чисел
. 2) Найти сумму и частное чисел 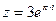 ,
, 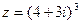 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 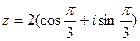 .
.
4) Найти все значения корня из комплексного числа 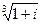 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 0 < Re z < 3, 0 < arg z < 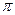 .
.
Вариант № 2.
1) Найти и изобразить геометрически на комплексной плоскости число 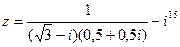 .
.
2) Найти сумму и частное чисел 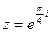 ,
, 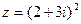 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 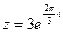 .
.
4) Найти все значения корня из комплексного числа 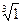 . Изобразить на окружности. 5) Изобразить на комплексной плоскости множество точек, которое определяется условиями:
. Изобразить на окружности. 5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 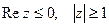 .
.
Вариант № 3
1) Найти и изобразить геометрически на комплексной плоскости число 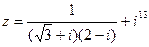 .
.
2) Найти сумму и частное чисел 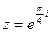 ,
, 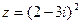 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 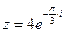 .
.
4) Найти все значения корня из комплексного числа 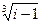 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 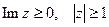 .
.
Вариант № 4
1) Найти и изобразить геометрически на комплексной плоскости число 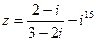 .
.
2) Найти сумму и частное чисел 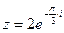 ,
, 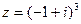 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 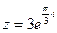 .
.
4) Найти все значения корня из комплексного числа 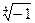 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 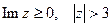 .
.
Вариант № 5
1) Найти и изобразить геометрически на комплексной плоскости число 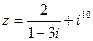 .
.
2) Найти сумму и частное чисел 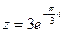 ,
, 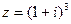 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 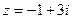 .
.
4) Найти все значения корня из комплексного числа 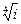 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 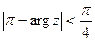 .
.
Вариант № 6
1) Найти и изобразить геометрически на комплексной плоскости число 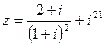 .
.
2) Найти сумму и частное чисел 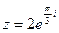 ,
, 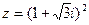 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 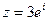 .
.
4) Найти все значения корня из комплексного числа 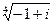 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 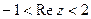 ,
, 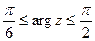 .
.
Вариант № 7
1) Найти и изобразить геометрически на комплексной плоскости число 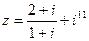 .
.
2) Найти сумму и частное чисел 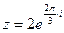 ,
, 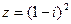 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 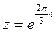 .
.
4) Найти все значения корня из комплексного числа 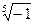 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 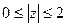 ,
, 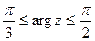 .
.
Вариант № 8
1) Найти и изобразить геометрически на комплексной плоскости число 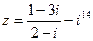 .
.
2) Найти сумму и частное чисел 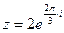 ,
, 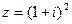 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 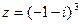 .
.
4) Найти все значения корня из комплексного числа 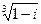 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 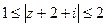 .
.
Вариант № 9
1) Найти и изобразить геометрически на комплексной плоскости число 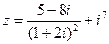 .
.
2) Найти сумму и частное чисел 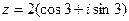 ,
, 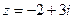 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 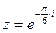 .
.
4) Найти все значения корня из комплексного числа 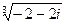 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 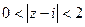 ,
, 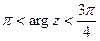 .
.
Вариант № 10
1) Найти и изобразить геометрически на комплексной плоскости число 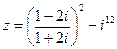 .
.
2) Найти сумму и частное чисел 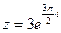 ,
, 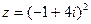 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 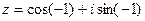 .
.
4) Найти все значения корня из комплексного числа 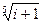 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 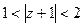 ,
, 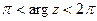 .
.
Вариант № 11
1) Найти и изобразить геометрически на комплексной плоскости число 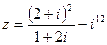 . 2) Найти сумму и частное чисел
. 2) Найти сумму и частное чисел 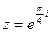 ,
, 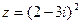 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 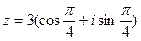 .
.
4) Найти все значения корня из комплексного числа 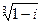 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 0 < Im z < 3, 0 < arg z < 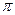 .
.
Вариант № 12
1) Найти и изобразить геометрически на комплексной плоскости число 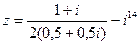 .
.
2) Найти сумму и частное чисел 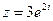 ,
, 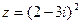 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 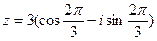 .
.
4) Найти все значения корня из комплексного числа 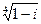 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 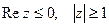 .
.
Вариант № 13
1) Найти и изобразить геометрически на комплексной плоскости число 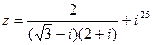 .
.
2) Найти сумму и частное чисел 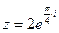 ,
, 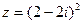 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 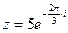 .
.
4) Найти все значения корня из комплексного числа 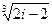 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 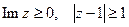 .
.
Вариант № 14
1) Найти и изобразить геометрически на комплексной плоскости число 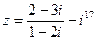 .
.
2) Найти сумму и частное чисел 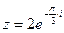 ,
, 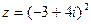 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 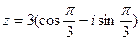 .
.
4) Найти все значения корня из комплексного числа 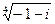 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 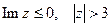 .
.
Вариант № 15
1) Найти и изобразить геометрически на комплексной плоскости число 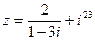 .
.
2) Найти сумму и частное чисел 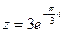 ,
, 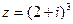 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 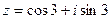 .
.
4) Найти все значения корня из комплексного числа 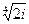 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 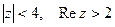 .
.
Вариант № 16
1) Найти и изобразить геометрически на комплексной плоскости число 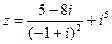 .
.
2) Найти сумму и частное чисел 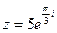 ,
, 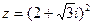 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 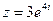 .
.
4) Найти все значения корня из комплексного числа 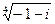 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 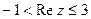 ,
, 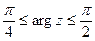 .
.
Вариант № 17
1) Найти и изобразить геометрически на комплексной плоскости число 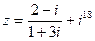 .
.
2) Найти сумму и частное чисел 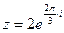 ,
, 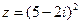 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 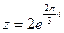 .
.
4) Найти все значения корня из комплексного числа 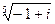 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 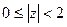 ,
, 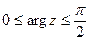 .
.
Вариант № 18
1) Найти и изобразить геометрически на комплексной плоскости число 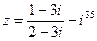 .
.
2) Найти сумму и частное чисел 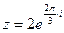 ,
, 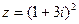 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 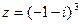 .
.
4) Найти все значения корня из комплексного числа 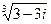 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 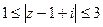 .
.
Вариант № 19
1) Найти и изобразить геометрически на комплексной плоскости число 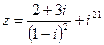 .
.
2) Найти сумму и частное чисел 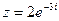 ,
, 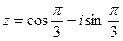 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 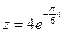 .
.
4) Найти все значения корня из комплексного числа 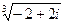 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 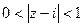 ,
, 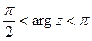 .
.
Вариант № 20
1) Найти и изобразить геометрически на комплексной плоскости число 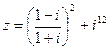 .
.
2) Найти сумму и частное чисел 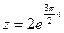 ,
, 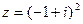 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 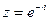 .
.
4) Найти все значения корня из комплексного числа 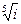 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 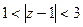 ,
, 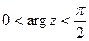 .
.
Вариант № 21
1) Найти и изобразить геометрически на комплексной плоскости число 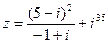 .
.
2) Найти сумму и частное чисел 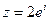 ,
, 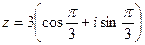 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 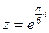 .
.
4) Найти все значения корня из комплексного числа 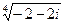 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 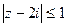 ,
, 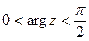 .
.
Вариант № 22
1) Найти и изобразить геометрически на комплексной плоскости число 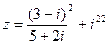 .
.
2) Найти сумму и частное чисел 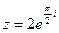 ,
, 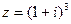 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 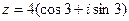 .
.
4) Найти все значения корня из комплексного числа 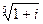 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 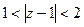 ,
, 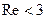 .
.
Вариант № 23
1) Найти и изобразить геометрически на комплексной плоскости число 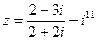 .
.
2) Найти сумму и частное чисел 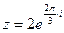 ,
, 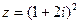 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 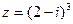 .
.
4) Найти все значения корня из комплексного числа 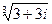 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 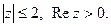
Вариант № 24
1) Найти и изобразить геометрически на комплексной плоскости число 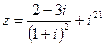 .
.
2) Найти сумму и частное чисел 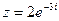 ,
, 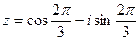 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 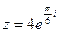 .
.
4) Найти все значения корня из комплексного числа 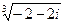 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 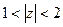 ,
, 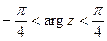 .
.
Вариант № 25
1) Найти и изобразить геометрически на комплексной плоскости число 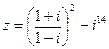 .
.
2) Найти сумму и частное чисел 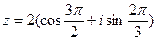 ,
, 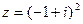 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 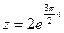 .
.
4) Найти все значения корня из комплексного числа 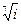 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 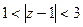 ,
, 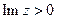 .
.
Вариант № 26
1) Найти и изобразить геометрически на комплексной плоскости число 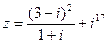 .
.
2) Найти сумму и частное чисел 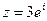 ,
, 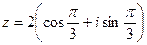 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 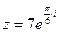 .
.
4) Найти все значения корня из комплексного числа 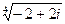 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 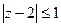 ,
, 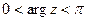 .
.
Вариант № 27
1) Найти и изобразить геометрически на комплексной плоскости число 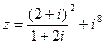 .
.
2) Найти сумму и частное чисел 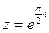 ,
, 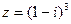 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 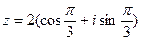 .
.
4) Найти все значения корня из комплексного числа 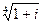 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 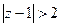 ,
, 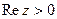 .
.
Вариант № 28
1) Найти и изобразить геометрически на комплексной плоскости число 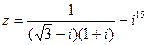 .
.
2) Найти сумму и частное чисел 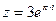 ,
, 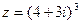 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 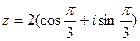 .
.
4) Найти все значения корня из комплексного числа 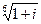 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 0 < Re z < 3, 0 < arg z < 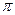 .
.
Вариант № 29.
1) Найти и изобразить геометрически на комплексной плоскости число 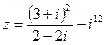 .
.
2) Найти сумму и частное чисел 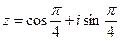 ,
, 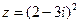 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 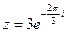 .
.
4) Найти все значения корня из комплексного числа 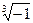 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 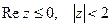 .
.
Вариант № 30
1) Найти и изобразить геометрически на комплексной плоскости число 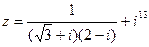 .
.
2) Найти сумму и частное чисел 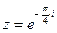 ,
, 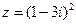 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 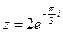 .
.
4) Найти все значения корня из комплексного числа 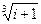 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 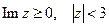 .
.
Вариант № 31
1) Найти и изобразить геометрически на комплексной плоскости число 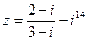 .
.
2) Найти сумму и частное чисел 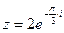 ,
, 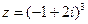 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 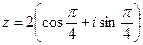 .
.
4) Найти все значения корня из комплексного числа 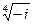 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 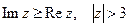 .
.
Вариант № 32
1) Найти и изобразить геометрически на комплексной плоскости число 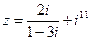 .
.
2) Найти сумму и частное чисел 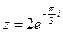 ,
, 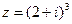 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 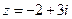 .
.
4) Найти все значения корня из комплексного числа 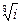 . Изобразить на окружности.
. Изобразить на окружности.
5) Изобразить на комплексной плоскости множество точек, которое определяется условиями: 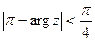 .
.
Вариант № 33
1) Найти и изобразить геометрически на комплексной плоскости число 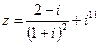 .
.
2) Найти сумму и частное чисел 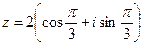 ,
, 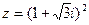 .
.
3) Найти действительную и мнимую части, модуль, аргумент числа, сопряженное комплексному числу 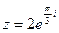 .
.
4) Найти все значения корня из комплексного числа 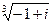 . Изобразить на окружности.
. Изобразить на окружности.
