Нелогичное развитие логичнейшей из наук

Нет, не оплакивать былое —

В нем силу надобно искать.

Уордсворт

На протяжении двух тысячелетий математики были уверены в том, что весьма успешно открывают математические принципы, заложенные в фундаменте мироздания. Но в середине XIX в. они вынуждены были признать, что глубоко заблуждались, принимая математические законы за абсолютные истины. В течение двух тысячелетий математики не сомневались, что неукоснительно следуют предложенной древнегреческими мыслителями схеме постижения истины, выводя с помощью дедуктивных рассуждений из математических аксиом следствия, не уступающие по надежности самим исходным аксиомам. Поскольку математические законы естествознания отличались необычайной точностью, редкие расхождения по поводу корректности некоторых математических рассуждений от «метались как не заслуживающие внимания. Даже самые проницательные и дальновидные математики были убеждены, что любой пробел в математическом доказательстве, если таковой обнаружится, может быть легко восполнен. Но в XIX в. единодушие математиков по поводу безупречной доказательности математических рассуждений явно поколебалось.

Что же открыло математикам глаза? Как они смогли понять, что заблуждались, полагаясь на безупречность математических рассуждений? Некоторые математики еще в начале XIX в. выражали озабоченность в связи с критикой, которой подвергались основные положения математического анализа, но большинство считало эти нападки недостаточно обоснованными и просто игнорировало их. Лишь появление неевклидовой геометрии и кватернионов, которые заставили математику отказаться от многовековых претензий на владение абсолютной истиной, побудило большинство математиков обратить внимание на пробелы в логике математических исследований.

Работы в области неевклидовой геометрии, которые сопровождались постоянными и столь естественными ссылками на аналогичные теоремы и доказательства евклидовой геометрии, привели к поразительному открытию: выяснилось, что евклидова геометрия, которую на протяжении двух тысячелетий специалисты провозглашали неподражаемым образцом строгих доказательств, обладает серьезными логическими изъянами! Создание новых алгебр, начало которому было положено введением кватернионов (гл. IV), настолько обеспокоило математиков, что им захотелось подвергнуть критическому пересмотру логические основы арифметики и алгебры обычных вещественных и комплексных чисел. Такой пересмотр действительно был необходим — хотя бы для того, чтобы убедиться в надежности представлений о свойствах этих чисел. Открытие, которое ожидало математиков в, казалось бы, хорошо известной им области, было поистине удивительным: эти разделы математики, традиционно считавшиеся в высшей степени логичными, развивались алогично!

Если хочешь разобраться в настоящем, следует прежде всего заглянуть в прошлое! Обратившись к прошлому, математики, чье восприятие обострилось в результате последних открытий, наконец увидели то, что ускользало от их предшественников или мимо чего те равнодушно проходили в своем безудержном стремлении постичь истину. Разумеется, математики отнюдь не собирались безропотно отказываться от своей науки. Помимо того что математические методы продолжали оставаться весьма эффективным инструментом естественнонаучного исследования, математика сама по себе превратилась в область знания, которую многие математики вслед за Платоном считали особой «внечувственной реальностью».[60]Естественно, математики сочли, что им под силу по крайней мере пересмотреть логическую структуру математики и восполнить пробелы в ней или изменить те ее области, где обнаружатся изъяны.

Как нам уже известно, родоначальниками дедуктивной математики были древние греки и первым, казалось бы, совершенным математическим построением стали «Начала» Евклида. Начав с определений и аксиом, Евклид далее переходил к доказательству теорем. Повторим, однако, некоторые из определений Евклида:

1. Точка есть то, что не имеет частей.

2. Линия же — длина без ширины.

3. Прямая линия есть та, которая равно расположена по отношению к точкам на ней. ([25], кн. I-VI, с. 11.)

Аристотель учил, что определение должно описывать определяемое понятие через другие, уже известные понятия. А так как с чего-то необходимо начать, утверждал Аристотель, то в качестве исходных необходимо принять какие-то неопределяемые понятия. Хотя, судя по многим данным, Евклид, живший и работавший в Александрии примерно в III в. до н.э., хорошо знал о работах греческих авторов классической эпохи, в частности Аристотеля, он тем не менее дал определение всемгеометрическим понятиям.

Этот просчет Евклида принято объяснять двумя причинами. Либо Евклид был не согласен с Аристотелем в том, что исходные понятия должны быть неопределяемыми, либо, как утверждают некоторые защитники Евклида, он сознавал необходимость неопределяемых понятий, но своими первыми определениями намеревался дать лишь интуитивное представление о смысле определяемых понятий, позволяющее понять последующие аксиомы. Но если справедливо последнее, то в таком случае Евклид вряд ли стал бы включать определения в основной текст «Начал». Каковы бы ни были намерения самого Евклида, никто из математиков, следовавших дедуктивному методу Евклида на протяжении двух тысячелетий, не отметил необходимость неопределяемых понятий. На необходимость таких понятий обратил внимание в своем «Трактате о геометрическом духе» (1658) Паскаль, но это его напоминание просто не было никем замечено.

А как обстояло дело с аксиомами Евклида? Следуя, по-видимому, Аристотелю, Евклид сформулировал ряд общих понятий, применимых к любому рассуждению, и пять постулатов, применимых только к геометрии. Одно из общих понятий гласило: «И если к равным [вещам] прибавляются равные, то и целые будут равны» ([25], кн. I-VI, с. 15). Под словом «вещи» Евклид понимал длины, площади, объемы и целые числа. Разумеется, это слово допускает весьма широкое толкование. Но еще в большей степени может вводить в заблуждение общее утверждение, что фигуры, совпадающие при наложении, равны. С помощью этой аксиомы Евклид доказывал конгруэнтность двух треугольников, налагая один треугольник на другой и выводя из известных геометрических фактов заключение о равенстве углов. Но чтобы наложить один треугольник на другой, его необходимо передвинуть. Евклид предполагал, что перемещение не сказывается на свойствах треугольника. Таким образом, общее понятие, задающее «принцип наложения», по существу, выражает однородность пространства, т.е. независимость свойств геометрических фигур от их расположения в пространстве. Такого рода допущение вполне разумно, но все же является дополнительным допущением: определения в евклидовых «Началах» не затрагивают понятия движения.[61]

В своих доказательствах Евклид нередко прибегал к аксиомам, явно им не сформулированным. Еще Гаусс обратил внимание на то, что Евклид говорит о точках, лежащих между другими точками, и о прямых, лежащих между другими прямыми, ни словом не обмолвившись о понятии «лежать между» и его свойствах. По-видимому, Евклид мысленно представлял геометрические фигуры и использовал в доказательствах теорем свойства реальных фигур, не отраженные в аксиомах. Наглядные геометрические представления могут оказаться весьма полезными и при доказательстве, и при запоминании теоремы, но роль их должна быть лишь вспомогательной. Лейбниц обратил внимание еще на одну аксиому, неявно использованную Евклидом, — аксиому о так называемой непрерывности. Действительно, Евклид широко пользовался тем, что прямая, соединяющая точку A, расположенную по одну сторону от l (рис. 5.1), с точкой B, расположенной по другую сторону от прямой l , имеет с l общую точку. Существование общей точки очевидно из чертежа — однако ни одна аксиома о прямых не гарантирует, что такая общая точка действительно имеется. Впрочем, можно ли говорить, что точки «находятся по разные стороны от прямой»? Подобное словоупотребление также основывается на неявно подразумеваемой, но неформулируемой аксиоме.

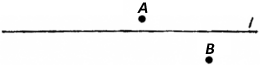
Рис. 5.1. Аксиома, которую не сформулировал Евклид.

Помимо различного рода изъянов и недостатков в определениях и аксиомах «Начала» Евклида содержали также много неадекватных доказательств. Доказательства одних теорем были ошибочными; доказательства других охватывали лишь частный случай утверждения теоремы или конфигурации, о которой в ней говорилось. Такого рода недостатки не столь серьезны, так как их легче исправить. Евклид умышленно проводил правильные доказательства для фигур, весьма отдаленно напоминающих изображаемые. Но если судить о «Началах» в целом, то с полным основанием можно сказать, что в ряде случаев доказательства Евклида, касающиеся легко воспроизводимых на чертежах фигур, имели дефекты. Короче говоря, логика в «Началах» Евклида оставляла желать лучшего.

Несмотря на все недостатки евклидовых «Начал», лучшие математики, естествоиспытатели и философы примерно до конца XVIII в. видели в них идеал математической строгости. Паскаль в своих «Мыслях» выразил это всеобщее восхищение так: «Геометрический дух во всем превосходит те предметы, которые поддаются законченному анализу. Он начинает с аксиом и выводит заключения, истинность которых может быть доказана с помощью универсальных логических правил». Учитель и предшественник Ньютона по кафедре в Кембриджском университете Исаак Барроу перечислил восемь причин непогрешимости геометрии: ясность геометрических понятий; однозначность определений; наша интуитивная уверенность в универсальной истинности общих геометрических понятий; правдоподобность и наглядность геометрических постулатов; малочисленность геометрических аксиом; ясное понимание способа получения всех величин; четкая последовательность доказательств; отказ от использования всего неизвестного. Такого рода признания достоинств геометрии можно было бы продолжить. В 1873 г. известный специалист по теории чисел Генри Джон Стивен Смит сказал: «Геометрия обратилась бы в ничто, если бы не ее строгость… Почти всеми признано, что методы Евклида безупречны с точки зрения строгости».

Тем не менее, работая над созданием неевклидовой геометрии, математики обнаружили в евклидовой схеме построения геометрии столь большое число дефектов, что восхищаться ее совершенством было уже невозможно. Неевклидова геометрия стала тем рифом, о который разбилась геометрия Евклида. То, что ранее казалось надежной твердью, в действительности оказалось предательской топью.

Разумеется, евклидова геометрия составляет лишь часть математики. С начала XVIII в. гораздо более обширной стала часть математики, посвященная свойствам чисел. Но как же развивалось логическое понятие числа?

В Древнем Египте и Вавилоне уже были хорошо знакомы с целыми числами, дробями и даже с такими иррациональными числами, как √ 2 или √ 3. Для практических приложений иррациональные числа аппроксимировали рациональными. Но поскольку математика в Древнем Египте, Вавилоне и даже вплоть до IV в. до н.э. в Древней Греции строилась на интуитивной или эмпирической основе, как восхищение ее логической структурой, так и ее критика были в равной степени беспредметны.

Первое известное нам логически последовательное изложение теории целых чисел содержится в VII, VIII и IX книгах «Начал» Евклида. В них Евклид предлагает, например, такие определения: «Единица есть [то], через что каждое из существующих считается единым; число же — множество, составленное из единиц» ([25], кн. VII-X, с. 9). Ясно, что подобные определения мало что говорят — в их формулировках отражается тот факт, что как в арифметике Евклида, так и в его геометрии проявляется непонимание необходимости неопределяемых понятий. При выводе свойств целых чисел Евклид использует уже упоминавшиеся общие понятия. К сожалению, некоторые из приведенных им доказательств ошибочны. Тем не менее древние греки и их преемники считали, что теория целых чисел обоснована вполне удовлетворительно. Более того, они, не церемонясь, позволяли себе говорить об отношениях целых чисел (у последующих поколений математиков такие отношения получили название дробей ), хотя отношения целых чисел не были ими никак определены.

В логическом развитии теории чисел древние греки столкнулись с трудностью, оказавшейся для них непреодолимой. Как известно, пифагорейцы в V в. до н.э. первыми подчеркнули важность целых чисел и отношений целых чисел для изучения природы. Более того, именно в целых числах и их отношениях пифагорейцы видели «меру» всего. Когда же обнаружилось, что некоторые отношения, например отношение гипотенузы равнобедренного прямоугольного треугольника к катету, непредставимы в виде отношения целых чисел, это и удивило, и обеспокоило пифагорейцов. Отношения, представимые в виде отношений целых чисел, пифагорейцы назвали соизмеримыми, а отношения, непредставимые в виде отношений целых чисел, получили название несоизмеримых. Так, иррациональное число √ 2 может служить примером несоизмеримого отношения. Открытие несоизмеримых соотношений легенда приписывает Гиппазию из Метапонта (V в. до н.э.). По преданию, в тот момент, когда Гиппазий пришел к этому открытию, пифагорейцы находились в открытом море — и они выбросили Гиппазия за борт, обвинив его в том, что он привнес в мироздание элемент, противоречивший пифагорейскому учению о сводимости всех явлений природы к целым числам или к их отношениям.

Доказательство того, что число √ 2 несоизмеримо с 1, т.е. иррационально, было предложено пифагорейцами. По Аристотелю, они доказали иррациональность √ 2 методом от противного (reductio ad absurdum), иначе говоря, избрали косвенный метод доказательства. Пифагорейцы показали, что если гипотенуза равнобедренного прямоугольного треугольника была бы соизмерима с катетом, то одно и то же число должно было бы быть и четным, и нечетным, что невозможно. Доказательство проводилось следующим образом. Предположим, говорили пифагорейцы, что отношение гипотенузы к катету представимо в виде a/b, где a и b — взаимно-простые целые числа (т.е. предполагается, что общие множители, которые первоначально могли входить в числа a и b, уже сокращены). Если a/b = √2, то a2 = 2b2 . Так как a2 — четное число, a также четно, поскольку квадрат любого нечетного числа нечетен.[62]Так как числитель и знаменатель отношения a/b не имеют общих делителей и a четно, число b должно быть нечетно. Число a как четное представимо в виде a = 2c, поэтому a2 = 4c2, а так как а2 = 2b2, то 4c2 = 2b2, или 2c2 = b2. Следовательно, b2 — четное число. Но тогда b также четное число, поскольку если бы оно было нечетным, то и квадрат его был бы нечетным. Но по доказанному ранее b — нечетное число; таким образом, мы приходим к противоречию.

Пифагорейцы и древнегреческие мыслители классического периода, как правило, не принимали иррациональных чисел, ибо в их понимании иррациональные числа не были числами. Действительно, предложенное пифагорейцами доказательство говорит, что число √ 2 непредставимо в виде отношения целых чисел, но умалчивает о том, что такое иррациональное число. Жители Древнего Вавилона, как уже отмечалось, умели работать с иррациональными числами, но они, безусловно, не знали, что используемые ими десятичные (точнее, шестидесятеричные) приближения таких чисел не могут быть абсолютно точными. Мы можем восхищаться жизнелюбием древних вавилонян, но математиками они были неважными. Совсем иной склад ума был у древних греков: они не могли довольствоваться приближениями.

Открытие иррациональных чисел поставило проблему, ставшую центральной для древнегреческой математики. Платон в своих «Законах» призывал к познанию несоизмеримых величин. Решение проблемы предложил Евдокс, некогда бывший учеником Платона: понятие величины надлежит трактовать геометрически. Длины, углы, площади и объемы, величины которых — если их выразить численно — могли оказаться иррациональными, следовало представлять геометрически. Именно так формулирует Евклид теорему Пифагора: квадрат, построенный на гипотенузе прямоугольного треугольника, равен сумме квадратов, построенных на обоих катетах. Под суммой квадратов Евклид понимает, что суммарная площадь фигуры, составленной из двух квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе. Обращение за помощью к геометрии здесь вполне понятно. Если числа 1 и √ 2 рассматривать как длины, т.е. как отрезки прямых, то принципиальное различие между 1 и √ 2 сглаживается и почти перестает быть заметным.

Проблема, возникшая в связи с появлением иррациональных чисел, была шире, чем проблема численного представления длин, площадей и объемов, так как корни квадратных уравнений, например уравнения x2 − 2 = 0, вполне могли быть иррациональными числами. Греки классического периода решали такие уравнения геометрически, т.е. представляли их корни в виде отрезков, тем самым избегая необходимости обращаться к иррациональным числам. Так, если у вавилонян существовала формула для решения квадратного уравнения, то у греков сходную роль играло построение отрезка x, удовлетворяющего, скажем, уравнению х2 + ax = b2. Это направление в развитии математики получило название геометрической алгебры. Таким образом, «Начала» Евклида — трактат не только по геометрии, но и по алгебре.

Превращение всей математики, за исключением разве лишь теории целых чисел, в геометрию привело к нескольким важным последствиям. Прежде всего оно усилило разрыв между теорией чисел и геометрией, ибо несоизмеримые величины целиком подлежали юрисдикции геометрии — арифметике (теории чисел) они были, так сказать, «неподсудны». Со времен Евклида между теорией чисел и геометрией приходилось проводить резкую границу.[63]А поскольку геометрия охватывала значительную часть математики, именно она и стала (по крайней мере до XVII в.) основой почти всей «строгой» математики. Мы до сих пор называем x2 «икс квадратом», x3 — «икс кубом», а не x соответственно во второй и в третьей степени, потому что некогда под x2 и x3 понимался лишь геометрический смысл этих величин.

Разумеется, геометрическое представление чисел и операций над ними не очень подходило для практических целей. Логически вполне удовлетворительно представлять произведение √2∙√3 как площадь прямоугольника. Но если требуется вычислить это произведение, то такого представления явно недостаточно. В естествознании и технике геометрические фигуры значительно менее полезны, чем численный ответ, полученный с требуемой точностью. В приложениях математики и в технике интерес представляют главным образом количественные результаты. Судоводителю в открытом море необходимо знать местоположение судна — численные значения его координат в градусах широты и долготы. Чтобы строить прочные и надежные здания, мосты, суда и плотины, также необходимо знать количественные меры длин, площадей и объемов деталей каждого сооружения. Более того, количественные характеристики, размеры, деталей сооружения необходимо знать заранее, до того как начнется постройка. Но греки классического периода, превыше всего ценившие строгие рассуждения и с пренебрежением относившиеся к приложениям математики в торговых расчетах, навигации, строительстве и составлении календарей, были удовлетворены полученным геометрическим решением проблемы иррациональных чисел.

На смену греческой цивилизации эпохи высокой классики (афинский период) около III в. до н.э. пришла эпоха эллинизма (александрийский период), сложившаяся в результате слияния классической греческой культуры с культурами Египта и Вавилона (гл. I). С точки зрения логики математика александрийского периода представляла собой любопытное смешение дедуктивных и эмпирических подходов. Наиболее выдающиеся математики александрийской эпохи Архимед и Аполлоний следовали образцу аксиоматической, дедуктивной геометрии «Начал» Евклида. Даже в своих трудах по механике Архимед начинал с аксиом и доказывал теоремы, став предтечей Ньютона и его последователей, создавших «математическую физику». Но под влиянием более прагматичных египтян и вавилонян александрийцы начали использовать математику и для удовлетворения запросов практики. В Александрии были выведены формулы, позволяющие вычислять количественные меры длин, площадей и объемов. Так, Герон (I в.) в своем сочинении «Метрика» привел формулу для вычисления площади S треугольника.[64]

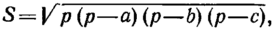
где a, b, c — длины сторон треугольника, p — его полупериметр. Вычисление площади треугольника по формуле Герона нередко приводит к иррациональным числам. Формула Герона замечательна еще в одном отношении: в отличие от греков эпохи высокой классики, которые считали бессмысленным произведение более чем трех чисел, поскольку ему нельзя было придать геометрический смысл, Герон был чужд подобных предрассудков. Во многих чистых и прикладных науках, развитых греческими учеными александрийского периода — составление календаря, измерение времени, навигационные расчеты, оптика, география, пневматика и гидростатика (гл. I), — иррациональные числа находили самое широкое применение.

Высшим достижением александрийцев стало создание Гиппархом и Птолемеем количественной астрономии — геоцентрической системы мира, позволившей человеку предсказывать движение планет, Солнца и Луны (гл. I). Для построения своей количественной теории Гиппарх и Птолемей разработали тригонометрию — область математики, занимающуюся вычислением одних элементов треугольника по данным о других его элементах. Так как подход Птолемея к построению тригонометрии отличался от принятого в то время, ему пришлось вычислять длины хорд окружности. Хотя для получения основных результатов об отношениях длин одних хорд к длинам других Птолемей использовал дедуктивно-геометрический метод, в процессе вычислений длин хорд (а именно они и были конечной целью расчетов) он широко применял арифметику и зачатки алгебры. Длины большинства хорд выражались иррациональными числами. Птолемей довольствовался получением рациональных приближений нужных ему величин, но в ходе вычислений, не колеблясь, употреблял и иррациональные числа.

Арифметика и алгебра, столь свободно используемые александрийцами, которым они достались по наследству от египтян и вавилонян, были лишены логической основы. Птолемей и другие ученые александрийского периода, как правило, перенимали у древних египтян и вавилонян эмпирический подход к математике. Такие иррациональные числа, как π , √2, √3 и другие, вводились некритически и в случае необходимости заменялись рациональными приближениями. Наиболее известный пример использования иррациональных чисел — приближенное вычисление Архимедом числа π. По оценкам Архимеда, значение π заключено между 31/7 и 310/71. Независимо от того, знал или нет Архимед, что число π иррационально, найденные им приближенные значения π содержали нескончаемые нагромождения квадратных корней ([33], с. 266-270, 528-553), а извлечение квадратного корня чревато появлением иррациональных чисел, о чем не мог не знать Архимед.

Для нашего повествования возрождение александрийскими математиками египетской и вавилонской алгебры, не зависящей от геометрии, имеет ничуть не меньшее значение, чем свободное использование иррациональных чисел. Выдающуюся роль в «оживлении» старой традиции сыграли Герон и еще один представитель александрийской школы — Диофант (примерно III в.). И Герон, и Диофант считали, что алгебраические и арифметические задачи представляют самостоятельный интерес и что обращение к геометрии излишне, поскольку не придает ни большей значимости задачам, ни большей логичности решениям. Герон формулировал и решал алгебраические задачи чисто арифметическими средствами. Например, дан квадрат, такой, что сумма его площади и периметра равна 896[65]; требуется найти сторону квадрата. Чтобы решить квадратное уравнение, к которому сводится задача, Герон добавляет к обеим частям полученного равенства по 4 и извлекает из них квадратный корень. Герон не доказывает правильности своих действий, а лишь указывает, в какой последовательности их надлежит выполнить. В работах Герона имеется немало задач такого рода.

В своей «Геометрике» Герон говорит о сложении площади круга, длины окружности и диаметра. Разумеется, под этим он понимает сложение численных значений этих величин. Говоря об умножении квадрата на квадрат, Герон также имеет в виду вычисление произведения тех чисел, которыми выражаются площади квадратов. Тем самым Герон как бы осуществил перевод многого из того, что достигла геометрическая алгебра древних греков, на язык арифметических и алгебраических операций. Некоторые из задач, рассмотренных Героном и его ближайшими последователями, в точности совпадают с задачами, встречающимися в вавилонских и египетских текстах за 2000 лет до н.э. Следует подчеркнуть, что свои алгебраические работы греки излагали в описательной манере. Ни к какой символике они не прибегали. Не приводили они и доказательств правильности используемых приемов. Со времен Герона задачи, приводящие к уравнениям, стали довольно распространенным типом головоломок.

В александрийский период алгебра достигла своего наивысшего расцвета в трудах Диофанта. О происхождении и жизни этого ученого почти ничего не известно. К сожалению, труды Диофанта, намного превосходившие по глубине и значимости сочинения его современников, появились слишком поздно, чтобы оказать сколько-нибудь заметное влияние на развитие математики того времени; разрушительная волна (гл. II) уже надвигалась, погребая под собой греческую цивилизацию. Несколько книг, написанных Диофантом, безвозвратно утеряно, однако шесть частей величайшего сочинения Диофанта «Арифметика», содержавшего, по утверждению самого автора, всего тринадцать частей, дошли до нашего времени [34]. Подобно египетскому папирусу Ринда, «Арифметика» Диофанта представляет собой сборник разрозненных задач. В посвящении говорится, что «Арифметика» задумана как серия задач, призванных помочь одному из учеников Диофанта овладеть различными видами чисел (Диофант [34], с. 41).

Одной из значительных заслуг Диофанта является введение в алгебру некоторой символики. Поскольку мы располагаем не подлинными рукописями самого Диофанта, а лишь поздними (датируемыми не ранее чем XIII в.) копиями, трудно говорить с уверенностью, какими именно символами пользовался сам Диофант. Известно лишь, что он ввел символы, соответствующие нашим обозначениям x, степеням неизвестного x вплоть до x6 и 1/x. Появление такой символики замечательно само по себе, но еще больший интерес представляет введение степеней выше третьей, поскольку, как мы уже отмечали, греки классического периода игнорировали произведения более чем трех сомножителей, так как считали их не имеющими геометрического смысла. Но если подходить к умножению с чисто арифметических позиций, то произведения более трех сомножителей, разумеется, становятся вполне законными. Именно такой подход к произведениям трех и более чисел был избран Диофантом.

Свои решения Диофант излагал словесно — так, как мы пишем прозу. Все необходимые действия он производил исключительно арифметически, не прибегая к геометрии для иллюстрации или в подтверждение своих рассуждений. Произведение (x − 1)(x − 2) Диофант вычислял чисто алгебраически, как это делаем мы. Использовал он и алгебраические тождества, например равенство a2 − b2 = (а − b)(a + b) и более сложные. Строго говоря, в своих вычислениях Диофант выполнял действия, основанные на использовании алгебраических тождеств, хотя сами тождества в явном виде у него не встречались.

Алгебра Диофанта обладала еще одной особенностью: Диофант охотно решал неопределенные уравнения, например одно уравнение с двумя неизвестными. Такие уравнения математики рассматривали и до Диофанта. Так, пифагорейцы нашли целочисленные решения уравнения[66] x2 + y2 = z2. Аналогичные уравнения рассматривались и в других сочинениях. Но Диофант был первым, кто предпринял систематические и обширные исследования неопределенных уравнений, став тем самым основателем нового раздела алгебры, называемого ныне диофантовым анализом .[67]

Хотя применение алгебры снискало Диофанту широкую известность, нельзя не отметить, что он признавал только положительные рациональные корни и отбрасывал все остальные. Даже при решении квадратного уравнения с одним неизвестным, имеющего два положительных рациональных корня, Диофант приводил только один (больший) корень. Если же уравнение имело два отрицательных корня, иррациональные или комплексные, то Диофант отвергал такое уравнение, считая его неразрешимым. Если уравнение, имело иррациональные корни, то Диофант шаг за шагом, от конца к началу, прослеживал полученное решение и показывал, как изменить исходное уравнение, чтобы новое уравнение имело рациональные корни. В этом Диофант отличался от Герона и Архимеда. Герон был инженером, и возникавшие в его расчетах иррациональные числа не пугали его. Для Герона иррациональные величины были вполне приемлемыми, хотя он, разумеется, и заменял их рациональными приближениями. Архимед также стремился получить точные решения и, если ответы выражались иррациональными числами, указывал границы, в которых те были заключены.

Нам не известно доподлинно, как Диофант пришел к своим уравнениям (см. [34]). Поскольку Диофант не пользовался геометрией, маловероятно, что он лишь переложил методы Евклида, приспособив их к решению квадратных уравнений. К тому же у Евклида не встречаются неопределенные уравнения: Диофант был первым из математиков, занявшихся систематическим исследованием таких уравнений. Мы не знаем, существовала ли преемственность в науке в конце александрийского периода, и поэтому нам трудно установить, в какой мере сказались на работах Диофанта идеи его древнегреческих предшественников. Использованные Диофантом методы решения уравнений имеют гораздо больше общего с традициями вавилонской математики. Ее влияние на Диофанта косвенно подтверждается и другими фактами. Однако алгебра Диофанта существенно отличается от вавилонской: Диофант ввел символику и стал систематически решать неопределенные уравнения. В целом деятельность Диофанта стала заметной вехой в истории алгебры.

Работы Герона и Диофанта, Архимеда и Птолемея по различным вопросам арифметики и алгебры не отличались по своему стилю от «рецептурных» текстов египтян и вавилонян, содержавших четкие указания относительно того, что и в какой последовательности следует делать. Дедуктивные, проводимые «по всей форме» доказательства геометрии Евклида, Аполлония и Архимеда были здесь преданы забвению. Все проблемы рассматривались индуктивно: автор указывал способ решения конкретной задачи, предположительно пригодный для решения более широкого круга задач, границы которого были нечетки. Нужно ли говорить, что при этом различные типы чисел (целые числа, дроби, иррациональные числа) вообще не определялись, если не считать маловразумительных определений целых чисел, предложенных Евклидом. Не существовало и аксиоматической основы, на которой можно было бы построить дедуктивную систему, пригодную для решения арифметических и алгебраических проблем.

Таким образом, греки завещали потомкам две совершенно различные математические науки: с одной стороны — дедуктивную, систематически развитую и излагаемую, хотя и не свободную от ошибок, геометрию, с другой — эмпирическую арифметику и алгебру как ее обобщение. Поскольку, согласно представлениям греческих мыслителей классического периода, математические результаты должны были выводиться дедуктивно и базироваться на явно заданной аксиоматической основе, возникновение независимых арифметики и алгебры, не обладающих собственной логической структурой, привело к одной из величайших аномалий в истории математики.

Индийцы и арабы, подхватившие эстафету развития математики после окончательного уничтожения арабами эллинистической (александрийской) греческой цивилизации, в еще большей мере нарушили концепцию математики, сложившуюся у греков классического периода. Подобно своим предшественникам — грекам, индийские и арабские математики использовали целые числа и дроби, но они, не колеблясь, оперировали и иррациональными числами. Именно они ввели новые, верные, правила сложения, вычитания, умножения и деления иррациональных чисел. Как же индийцам и арабам удалось придумать правила, лишенные логического обоснования и тем не менее оказавшиеся верными? Загадка решается довольно просто: индийцы и арабы рассуждали по аналогии. Так, правило √ab = √a∙√b они считали верным для любых чисел a и b, поскольку оно выполнялось, например, в случае √36 = √4∙√9. Фактически индийцы считали, не оговаривая этого специально, что с квадратными корнями из целых чисел можно обращаться так же, как с целыми числами.

Индийцы были менее изощренными математиками, чем греки, и не видели, какие логические трудности таятся в понятии иррационального числа. Интересуясь «рецептурной», или алгоритмической, стороной вычислений, индийцы не заметили те различия, которым греки придавали столь большое значение. Но производя сложение и вычитание, умножение и деление иррациональных чисел по таким же правилам, по каким производятся арифметические операции над рациональными числами, индийцы внесли посильный вклад в развитие математики. Кроме того, вся их арифметика была полностью независимой от геометрии.

Введя в обращение отрицательные числа для обозначения денежных долгов, или пассива, индийцы преумножили и без того многочисленные логические трудности математиков (положительные числа при таком подходе должны означать наличность, или актив). Первым ввел отрицательные числа Брахмагупта (около 628 г.), но он лишь сформулировал правила четырех арифметических действий над отрицательными числами, не приведя никаких определений, аксиом или теорем. Выдающийся индийский математик XII в. Бхаскара обратил внимание на то, что квадратный корень из положительного числа имеет два значения — положительное и отрицательное. Бхаскара рассмотрел также вопрос о квадратном корне из отрицательных чисел и пришел к выводу, что такой корень не существует, так как иначе его квадрат должен был бы быть отрицательным числом, а отрицательное число не может быть квадратом.

Далеко не все индийцы восприняли нововведение Бхаскары. Даже сам Бхаскара, приводя в качестве решений одной задачи два числа (50 и −50), утверждал: «Второе значение следует отбросить как неприемлемое, ибо люди не одобряют отрицательных решений». Тем не менее отрицательные числа вскоре после того, как они были введены, начали распространяться все шире.

Индийцам удалось достичь некоторых успехов и в алгебре. Для описания операций и неизвестных они ввели сокращенные слова и специальные символы, И хотя символика индийцев не была всеобъемлющей, их алгебра обладала определенными преимуществами по сравнению с алгеброй Диофанта. Решая задачу, индийцы указывали только основные этапы решения, не приводя никаких обоснований или доказательств. Отрицательные и иррациональные корни квадратных уравнений индийцы рассматривали наряду с положительными и рациональными корнями.