Задания для самостоятельного решения. 1.2. Упростите выражение:
I уровень
1.1. Вычислите:
1) 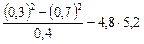 ; 2)
; 2) 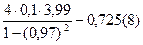 ;
;
3) 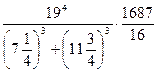 .
.
1.2. Упростите выражение:
1) 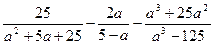 ;
;
2) 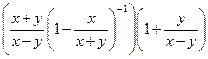 ;
;
3) 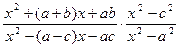 .
.
1.3. Известно, что 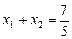 и
и 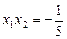 . Найдите:
. Найдите:
1) 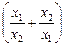 ; 2)
; 2) 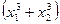 .
.
1.4. Докажите, что при 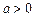 и
и 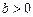 , дробь
, дробь 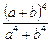 – неправильная.
– неправильная.
1.5. Разложите по формуле бинома Ньютона:
1) 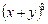 ; 2)
; 2) 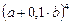 ; 3)
; 3) 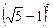 .
.
II уровень
2.1. Упростите выражение:
1) 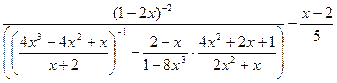 ;
;
2) 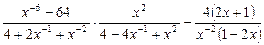 .
.
2.2. Известно, что 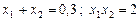 , найдите:
, найдите:
1) 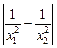 ; 2)
; 2) 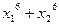 .
.
2.3. Докажите, что
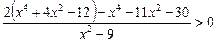 , при любых
, при любых 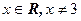 .
.
2.4. Разложите по формуле бинома Ньютона и упростите полученное выражение:
1) 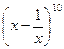 ; 2)
; 2) 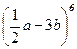 ; 3)
; 3) 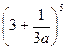 .
.
2.5. Вычислите:
1) 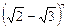 ; 2)
; 2) 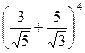 ; 3)
; 3) 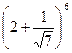 .
.
III уровень
3.1. Определить знак выражения при а >1:
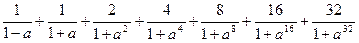 .
.
3.2. Сократите дробь:
1) 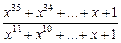 ; 2)
; 2)
3.3. Найдите значение выражения 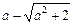 , если
, если 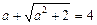 .
.
3.4. Вычислите значение выражения
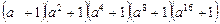 при
при 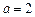 .
.
3.5. Докажите, что
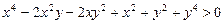 при любых х; у.
при любых х; у.
3.6. Упростите выражение 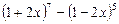 .
.
3.7. Найдите разность между коэффициентом и биноминальным коэффициентом при 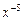 для выражения
для выражения 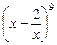 .
.
Многочлены. Действия над многочленами
Выражение вида
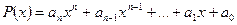 , (3)
, (3)
где 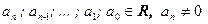
называется многочленом n-ой степени от одной переменной х, записанным в стандартном виде.
Числа 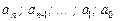 называются коэффициентами данного многочлена,
называются коэффициентами данного многочлена, 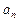 – старшим коэффициентом,
– старшим коэффициентом, 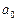 – свободным членом.
– свободным членом.
Если необходимо указать степень многочлена 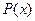 , то пишут
, то пишут 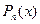 .
.
Если 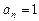 , то
, то 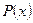 называется приведенным многочленом.
называется приведенным многочленом.
Если кроме 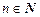 рассмотреть случай
рассмотреть случай 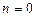 , то многочлен вида
, то многочлен вида 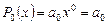 называется многочленом нулевой степени, он есть число.
называется многочленом нулевой степени, он есть число.
Каждое слагаемое вида 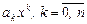 многочлена (3) называется одночленом.
многочлена (3) называется одночленом.
Два многочлена, заданные в виде (3), называются равными, если равны все их коэффициенты при соответствующих степенях переменной х.
Для всякого многочлена 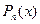 и многочлена
и многочлена 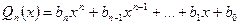 определены следующие операции:
определены следующие операции:
1) Умножение на число 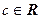 :
:
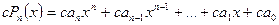 ;
;
2) Сложениемногочленов:
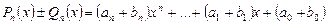 ;
;
3. Умножениемногочленов производят по следующему правилу: каждый член одного многочлена умножают на каждый член второго многочлена и приводят подобные. 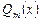 и привести подобные.
и привести подобные.
4. Деление многочленов (при условии, что степень делителя меньше или равна степени делимого) выполняется по правилу «деления углом» (см. далее пример ).
Результат деления записывается в виде:
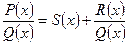 или
или
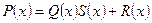 (4)
(4)
где 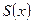 – частное (многочлен),
– частное (многочлен), 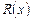 – остаток (степень остатка меньше степени делителя).
– остаток (степень остатка меньше степени делителя).
Многочлен 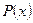 делится нацело на
делится нацело на 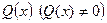 , если
, если 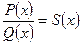 или
или
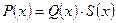 .
.
Если 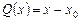 , где
, где 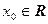 , то результат деления многочлена
, то результат деления многочлена 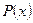 на
на 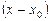 , согласно формуле (4), можно записать в виде равенства
, согласно формуле (4), можно записать в виде равенства
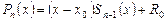 , (5)
, (5)
где R0 – число.
Коэффициенты многочлена 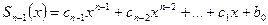 и остаток R0 в Равенстве (5) можно вычислить по схеме Горнера:
и остаток R0 в Равенстве (5) можно вычислить по схеме Горнера:
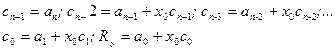 (6)
(6)
При вычислении коэффициентов (6) используют таблицу:
| an | an-1 | an-2 | . . . | a1 | a0 | |
| x0 | сn-1 | сn-2 | сn-3 | . . . | с0 | R0 |
Верхняя строка заполняется коэффициентами заданного многочлена (3), нижняя – числами, которые вычисляют по формулам (6).
Число 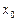 ,
, 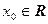 называется корнем многочлена
называется корнем многочлена 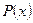 , если
, если 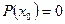 .
.
Число 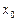 называется корнем кратностиk многочлена
называется корнем кратностиk многочлена 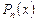 , если
, если
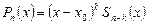 и
и 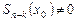 .
.
Теорема 1. (Безу).
Число х0 является корнем многочлена 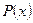 , тогда и только тогда, когда
, тогда и только тогда, когда 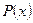 делится нацело на
делится нацело на 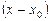 .
.
Теорема 2.
Число 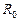 является остатком от деления многочлена
является остатком от деления многочлена 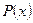 на
на 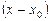 , тогда и только тогда, когда
, тогда и только тогда, когда 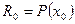 .
.
Теорема 3.
Пусть 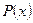 – приведенный многочлен с целыми коэффициентами. Если он имеет целые корни, то они содержатся среди целых делителей свободного члена.
– приведенный многочлен с целыми коэффициентами. Если он имеет целые корни, то они содержатся среди целых делителей свободного члена.
Представление многочлена 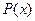 в виде произведения двух или нескольких многочленов (если это возможно) называется разложением
в виде произведения двух или нескольких многочленов (если это возможно) называется разложением 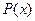 на множители.
на множители.
Общий вид разложения 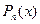 на множители:
на множители: 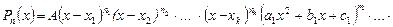
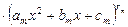 ,
,
где А, a1; …; b1; …; c1; … 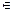 R (const);
R (const);
х1; х2; …; хk – корни многочлена 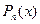 .
.
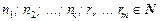 ;
;
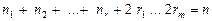 ;
;
квадратные трехчлены не имеют действительных корней.
Основные методы разложения:
1) вынесения общего множителя за скобки;
2) метод группировки
– непосредственно;
– с предварительными преобразованиями слагаемых;
3) использование формул сокращенного умножения;
4) использование формул разложения квадратного трехчлена на множители 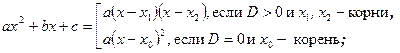
5) выделение полного квадрата и сведение к разности квадратов;
6) введение новой переменной;
7) поиск корней многочлена среди делителей свободного члена, использование теоремы Безу.
Многочлен может зависеть не только от одной переменной, но и от двух 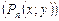 ; трех
; трех 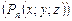 и т.д. Данные многочлены называются многочленами от нескольких переменных. Тогда их одночленом называют выражение, представляющее собой произведение чисел и переменных в некоторых степенях. Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Старшая степень многочлена нескольких переменных определяется старшей степенью его одночлена.
и т.д. Данные многочлены называются многочленами от нескольких переменных. Тогда их одночленом называют выражение, представляющее собой произведение чисел и переменных в некоторых степенях. Степенью одночлена называют сумму показателей степеней всех входящих в него переменных. Старшая степень многочлена нескольких переменных определяется старшей степенью его одночлена.
Многочлен от двух переменных 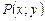 называется симметрическим, если при замене переменных x на у и у на x выражение
называется симметрическим, если при замене переменных x на у и у на x выражение 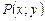 не меняется.
не меняется.
Над многочленами от нескольких переменных можно выполнять действия, аналогичные действиям над многочленами от одной переменной. Для разложения данных многочленов на множители применяются те же методы, что и длямногочленов от одной переменной.
Пример 1.Представить многочлен в стандартном виде, определить его степень:
1) 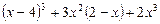 ; 2)
; 2) 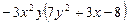 .
.
Решение.
- Раскроем скобки и приведем подобные:
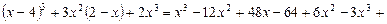
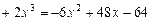 .
.
Данный многочлен является многочленом 2-й степени относительно х.
2. Умножим многочлен на одночлен
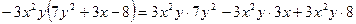 .
.
Приведем подобные и получаем многочлен
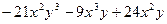 ,
,
который является многочленом 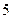 -й степени от двух переменных х, у (наибольшее суммарное значение показателей имеем в первом одночлене:
-й степени от двух переменных х, у (наибольшее суммарное значение показателей имеем в первом одночлене: 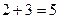 ).
).
Пример 2. Найти частное и остаток от деления многочлена 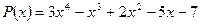 на многочлен
на многочлен 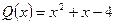 . Результат деления записать в виде равенства.
. Результат деления записать в виде равенства.
Решение.
Воспользуемся правилом «деления углом»:
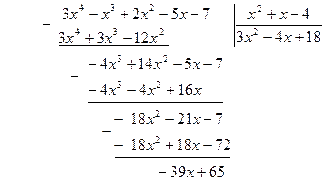
Получаем:
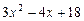 – частное (целая часть);
– частное (целая часть);
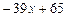 – остаток (многочлен первой степени).
– остаток (многочлен первой степени).
Тогда
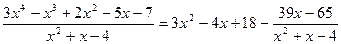 .
.
Пример 3. Проверить, делится ли многочлен 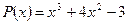 нацело на
нацело на 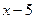 .Если нет, то найти значение остатка (не выполняя деления).
.Если нет, то найти значение остатка (не выполняя деления).
Решение.
У данного многочлена 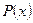 свободный член есть число
свободный член есть число 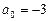 . Поскольку число 5 не является делителем числа
. Поскольку число 5 не является делителем числа 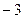 , то
, то 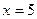 – не является корнем многочлена
– не является корнем многочлена 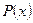 (см. теорему 3). Значит, согласно теореме 1,
(см. теорему 3). Значит, согласно теореме 1, 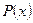 не разделится нацело на
не разделится нацело на 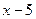 .
.
Остаток находим по теореме ??????????
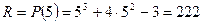 .
.
Пример 4. Разложить многочлен на множители:
1) 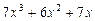 ; 2)
; 2) 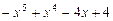 ;
;
3) 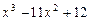 ; 4)
; 4) 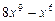 ;
;
5) 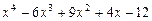 ; 6)
; 6) 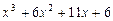 ;
;
7) 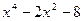 .
.
Решение.
1. Используем метод вынесения общего множителя за скобки:
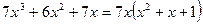 .
.
Поскольку у квадратного трехчлена 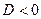 , то получен ответ.
, то получен ответ.
2. Воспользуемся методом группировки:
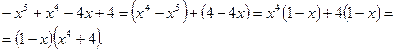 Для дальнейшего разложения выделим полный квадрат и сведем
Для дальнейшего разложения выделим полный квадрат и сведем 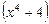 к разности квадратов:
к разности квадратов:
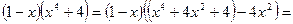
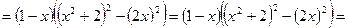
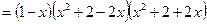 .
.
Поскольку дискриминанты квадратных трехчленов отрицательны, окончательно получаем разложение
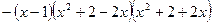 .
.
3. Вначале преобразуем данное выражение, а затем используем метод группировки и формулу разности квадратов

Вычисляем корни полученного квадратного трехчлена
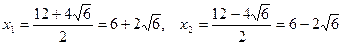 .
.
Поэтому 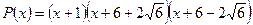
4. Вынесем общий множитель за скобки и воспользуемся формулой разности кубов:
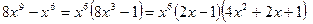 .
.
Получили искомое разложение.
5. Для многочлена 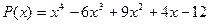 запишем целые делители свободного члена:
запишем целые делители свободного члена: 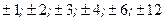 (см. теорему 3).
(см. теорему 3).
Подставим данные значения вместо 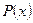 , убеждаемся, что
, убеждаемся, что 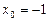 является корнем, т.к.
является корнем, т.к. 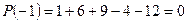 .
.
Разделим заданный многочлен на 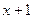 :
:
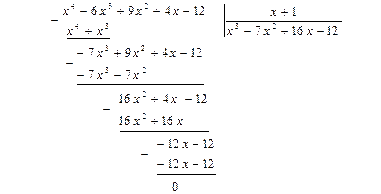
Получаем 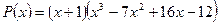 .
.
Для многочлена 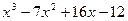 выполним аналогичные действия.
выполним аналогичные действия.
Проверкой делителей свободного члена находим корень 2.
Делим:
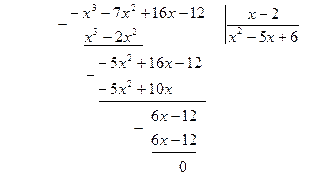
Тогда 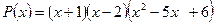
Квадратный трехчлен 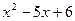 разлагаем на множители, используя формулы корней.
разлагаем на множители, используя формулы корней.
Окончательно получаем: 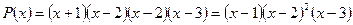 .
.
6. Для многочлена 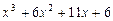 найдем целый корень среди делителей свободного члена
найдем целый корень среди делителей свободного члена 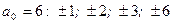 . Это число
. Это число 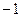 . Для дальнейшего разложения воспользуемся схемой Горнера:
. Для дальнейшего разложения воспользуемся схемой Горнера:
х3 х2 х1 х0
| х+1 | ||||
| -1 |
х2 х1 х0
Таким образом, 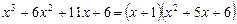 . Квадратный трехчлен
. Квадратный трехчлен 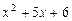 имеет корни
имеет корни 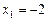 и
и 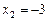 , а потому окончательно получаем:
, а потому окончательно получаем:
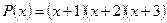 .
.
7. Для разложения многочлена 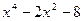 воспользуемся методом введения новой переменной. Пусть
воспользуемся методом введения новой переменной. Пусть 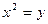 . Тогда имеем
. Тогда имеем 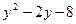 . Корни этого многочлена – числа
. Корни этого многочлена – числа 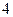 и
и 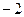 . Поэтому
. Поэтому 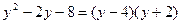 . Возвращаясь к старой переменной, имеем
. Возвращаясь к старой переменной, имеем
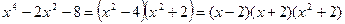 .
.
Пример 5. Найти a и b из заданного равенства и доказать, что a+b=0
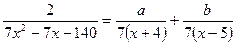 .
.
Решение.
Приведем правую часть заданного равенства к общему знаменателю:
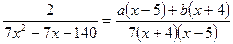
или
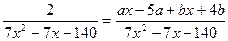 .
.
Поскольку знаменатели дробей равны, приравняем числители и сгруппируем в правой части коэффициенты при х. Многочлен в правой части запишем в стандартном виде.
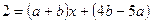 .
.
Из определения равенства многочленов получаем систему и решаем ее:
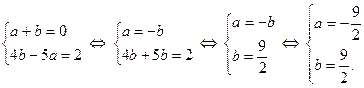
Находим сумму
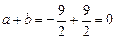 .
.
Доказательство завершено.
