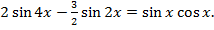Задания для самостоятельного решения

Решить системы уравнений:

1)

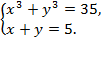
Ответ: х₁ = 2, у₁ = 3 или х₂ = 3, у₂ = 2;

2)

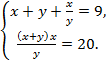
Ответ: 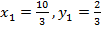или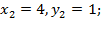

3)

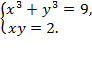
Ответ: х₁ = 1, у₁ = 2 или х₂ = 2, у₂ = 1;

4)

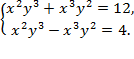
Ответ: х = 1, у = 2;

5)

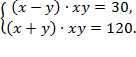
Ответ: х = 5, у = 3;

6)

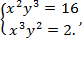
Ответ: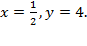

7)

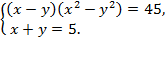
Ответ: х₁ = 4, у₁ = 1 или х₂ = 1, у₂ = 4;

8)

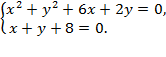
Ответ: х₁ = – 6, у₁ = –2 или х₂ = – 4, у₂ = – 4;

9)

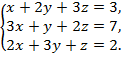
Ответ: х = 2, у = –1, z = 1;

10)

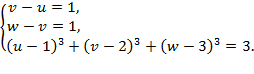
Ответ: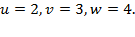

ВАРИАНТЫ ПИСЬМЕННОГО ВСТУПИТЕЛЬНОГО ЭКЗАМЕНА ПО МАТЕМАТИКЕ.

Вариант 1

1.Двое рабочих, действуя одновременно, выполнили задание за 5 дней. Если бы первый работал вдвое быстрее, а второй – вдвое медленнее, то работа заняла бы у них 4 дня. За сколько времени выполнил бы всю работу один первый рабочий?

2. Решить уравнение:

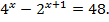
3. Доказать:

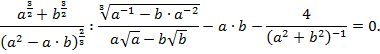
4. Решить уравнение:

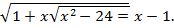
5. Решить уравнение:

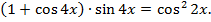
6. Построить область решения системы неравенств:

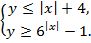
7. Найти наибольшее и наименьшее значение функции f (x) = y на отрезке [a, b].

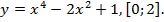
Вариант 2

1. Вычислить:

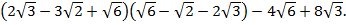
2. Решить уравнение:

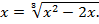
3. Решить уравнение:

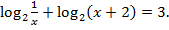
4. Решить неравенство:

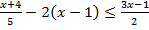
5. Имеются два раствора кислоты разной концентрации. Объем одного раствора 4 л, другого – 6 л. Если их слить вместе, то получится 35%-й раствор кислоты. Если же слить равные объемы этих растворов, то получится 36%-й раствор кислоты. Сколько литров кислоты содержится в каждом из первоначальных растворов?

6. Найти объем правильной треугольной пирамиды, сторона основания которой равна λ и образует с боковой гранью угол β.

7. Найти область решения системы на плоскости ХОУ:

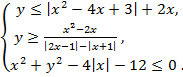
8. Решить уравнение:

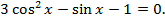
9. Решить уравнение:

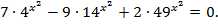
Вариант 3

1. Два велосипедиста одновременно выезжают из пункта А, направляясь в пункт В, расположенный в 56 км от А. Второй велосипедист отстает от первого каждый час на 2 км и прибывает в пункт В на 30 минут позже, чем первый. С какой скоростью едет каждый велосипедист?

2. Радиус основания конуса относится к высоте конуса как b : l. Площадь основания конуса равна S. Найти объем конуса.

3. Решить уравнение:

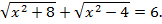
4. Решить уравнение:

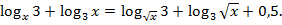
5. Найти на плоскости ХОУ область решения системы:

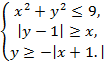
6. Найти площадь, ограниченную линиями:

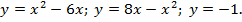
7. Решить уравнение:

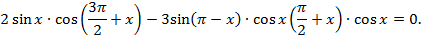
Вариант 4

1. Расстояние между станцией и поселком равно 4 км. Мальчик и автомобиль отправились одновременно со станции в поселок. Через 10 минут мальчик встретил автомобиль, возвращающийся из поселка. Когда мальчик прошел 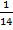км от места встречи, автомобиль, который дошел до станции и опять направился в поселок, нагнал мальчика. Найти их скорости, если известно, что они двигались равномерно и не делали остановок.

2. Диагонали осевого сечения усеченного конуса точкой пересечения делят в отношении 2:1, считая от большого основания. Угол между диагоналями, обращенный к основаниям конуса, равен α. Длина диагонали равна L. Найти объем усеченного конуса.

3. Решить уравнение:

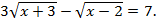
4. Решить уравнение:

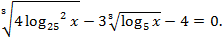
5. Найти на плоскости ХОУ область решения системы:

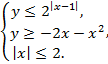
6. Найти площадь, ограниченную линиями:

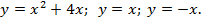
7. Решить уравнение: