Определение мощности множества всех подмножеств конечного множества (с использованием формулы бинома Ньютона)
Пусть А произвольное конечное n- элементное множество. Найдем мощность множества P(A), |P(А)|= 
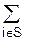
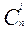 , где S={0,1,...,n}.
, где S={0,1,...,n}.
Для определения величины |Р(А)| воспользуемся формулой бинома Ньютона.
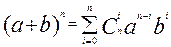 , при условиях, что a=в=1.
, при условиях, что a=в=1.
Получаем, 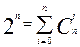 =|P(A)|.
=|P(A)|.
Замечание.
Множество 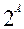 называется булеаноммножества А.
называется булеаноммножества А.
Понятия алгебраических и кардинальных операций. Алгебраические операции над множествами. Покрытие и разбиение множества.
Алгебраическимиоперациями называют такие, при выполнении которых результирующее множество либо пусто, либо состоит из элементов, из которых состоят и множества, подвергающиеся операциям.
Кардинальными операциями называют такие операции, при выполнении которых появляются новые элементы.
Основными алгебраическими операциями над множествами являются следующие:
- пересечение множеств,
- объединение множеств.
-разность множеств.
Пусть А и В - произвольные множества. Их пересечением называется множество
А 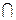 В={x| x
В={x| x  A и x
A и x  B}.
B}.
Объединениеммножеств А и В называется множество
А  В={x|x
В={x|x  A или x
A или x  B}.
B}.
Разностьюмножеств А и В называется множество А\В={x|x  A, но x
A, но x 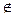 B}.
B}.
Используя понятие универса, можно ввести еще две операции над множествами - дополнение и симметрическую разность множеств.
Дополнением множества А (до универса J) называется множество 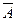 =J\A, т.е.
=J\A, т.е. 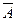 ={x| x
={x| x  J, но x
J, но x 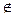 A}.
A}.
Симметрической разностьюмножеств А и В называется множество
А  В=(A\B)
В=(A\B)  (B\A).
(B\A).
Если А 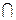 В=
В=  , то говорят, что множества А и В не пересекаются.
, то говорят, что множества А и В не пересекаются.
Если X - некоторое множество и X=A  В
В  ...
...  С, то множества А,В,...,С образуют покрытие множества X. Если при этом все множества А,В,...,С попарно не пересекаются, то система множеств А,В,...,С называется разбиением множестваX.
С, то множества А,В,...,С образуют покрытие множества X. Если при этом все множества А,В,...,С попарно не пересекаются, то система множеств А,В,...,С называется разбиением множестваX.
Поэлементное доказательство теоретико-множественных равенств.
Пусть А и В некоторые множества. Для того, чтобы проверить являются ли они равными, необходимо установить два соответствия : А  В и В
В и В  А.
А.
Для установления соответствия А  В необходимо показать, что текущий (т.е. произвольный) элемент множества А принадлежит множеству В. Такое доказательство называется поэлементным.
В необходимо показать, что текущий (т.е. произвольный) элемент множества А принадлежит множеству В. Такое доказательство называется поэлементным.
Покажем, например, справедливость утверждения:
(А  В)\ (А
В)\ (А 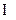 В)= (А\В)
В)= (А\В)  (В\А).
(В\А).
Пусть N=(А  В)\(А
В)\(А 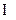 В), M=(А\В)
В), M=(А\В)  (В\А).
(В\А).
Надо показать, что N M и M
M и M N.
N.
Покажем, что N M.
M.
Пусть x  N, т.е. x
N, т.е. x  (А
(А  В), но x
В), но x 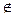 (А
(А 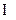 В).
В).
Если x 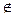 А и x
А и x  (А
(А  В), то x
В), то x  В, а отсюда x
В, а отсюда x  B\A.
B\A.
Если x 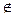 B и x
B и x  (А
(А  В), то x
В), то x  A, а отсюда x
A, а отсюда x  A\B.
A\B.
Получили, что всегда x принадлежит либо (А\В) либо (В\А), т.е x  M.
M.
Покажем, что M N.
N.
Пусть x  M, т.е. x
M, т.е. x  А\В или x
А\В или x  В\А.
В\А.
Если x  А\В, то x
А\В, то x  А и тем самым x
А и тем самым x  А
А  В.
В.
Так как x 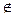 В, то x
В, то x 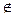 А
А 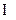 В, а тем самым x
В, а тем самым x  (А
(А  В)\ (А
В)\ (А 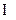 В)=N.
В)=N.
Аналогично доказывается и для случая x  В\А.
В\А.
