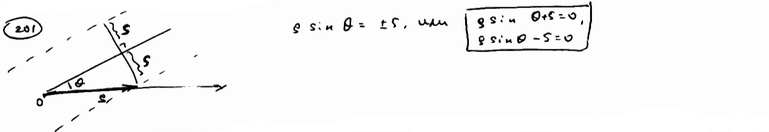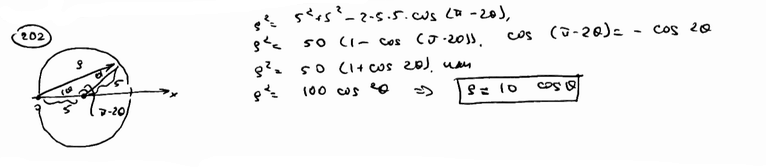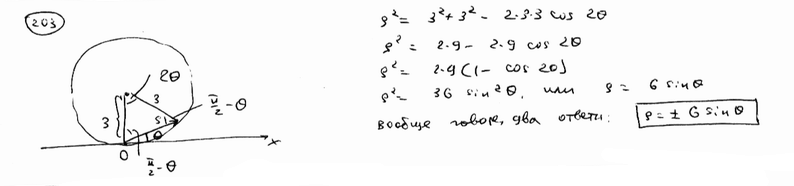| | | Вывести уравнение геометрического места точек, одинаково удаленных от координатных осей.  |
| | | Вывести уравнение геометрического места точек, находящихся на расстоянии а от оси Оу.  |
| | | Вывести уравнение геометрического места точек, находящихся на расстоянии b от оси Ох.  |
| | | Из точки Р(6; -8) проведены всевозможные лучи до пересечения с осью абсцисс. Составить уравнение геометрического места их середин. 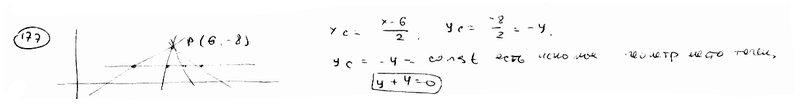 |
| | | Из точки С(10; -3) проведены всевозможные лучи до пересечения с осью ординат. Составить уравнение геометрического места их середины.  |
| | | Вывести уравнение траектории точки, которая в каждый момент движения одинаково удалена от точек: |
| | 179.1 | А(3; 2) и В(2; 3); |
| | 179.2 | А(5; -1) и В(1; -5); |
| | 179.3 | А(5; -2) и В(-3; -2); |
| | 179.4 | А(3; -1) и В(3; 5).  |
| | | Составить уравнение геометрического места точек, разность квадратов расстояний которых до точек А(-а; 0) и В(а; 0) равна с. 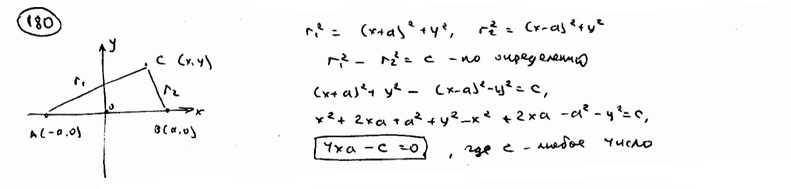 |
| | | Вывести уравнение окружности, имеющей центр в начале координат и радиус r.  |
| | | Вывести уравнение окружности, имеющей, имеющей центр С( 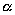 ; ; 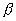 ) и радиус r. ) и радиус r.  |
| | | Дано уравнение окружности 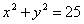 . Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8. . Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8.  |
| | | Составить уравнение геометрического места точек, сумма квадратов расстояний которых до точек А(-3; 0) и В(3; 0) равна 50. 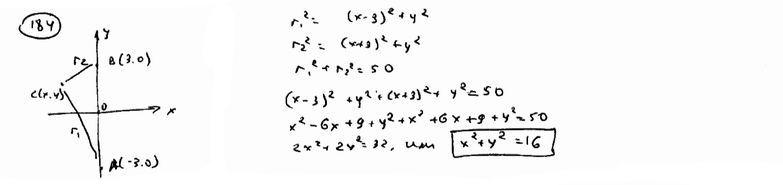 |
| | | Ввершины квадрата суть точки А(а; а), В(-а; а), С(-а; -а) и D(а; -а). Составить уравнение геометрического места точек, сумма квадратов расстояний которых до сторон этого квадрата есть величина постоянная, равна 6а2. 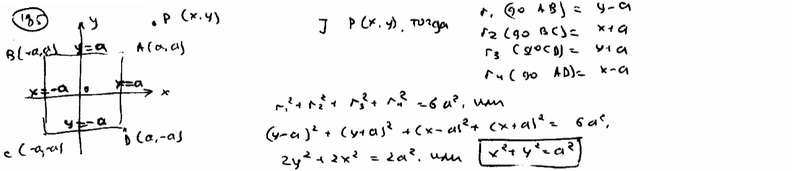 |
| | | Через начало координат проведены всевозможные хорды окружности 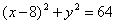 . Составить уравнение геометрического места середин этих хорд. . Составить уравнение геометрического места середин этих хорд. 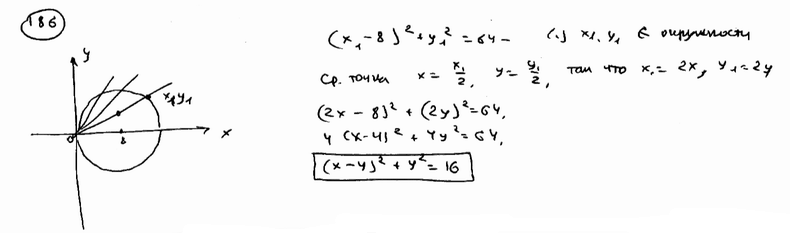 |
| | | Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F1(-3; 0), F2(3; 0) есть величина постоянная, равная 10. 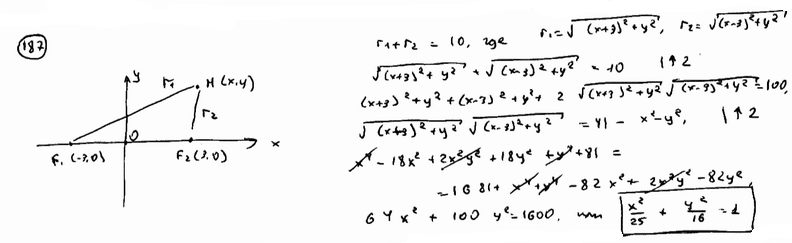 |
| | | Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F1(-5; 0), F2(5; 0) есть величина постоянная, равная 6. 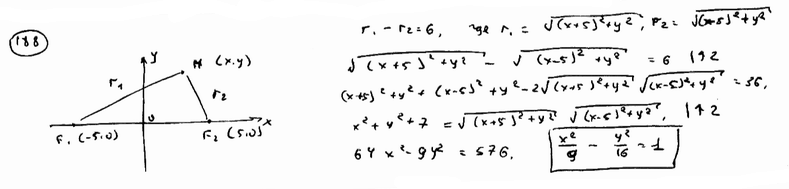 |
| | | Вывести уравнение геометрического места точек, для которых расстояние до данной точки F(3; 0) равно расстоянию до данной прямой 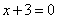 . . 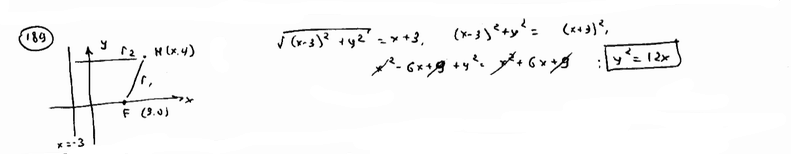 |
| | | Вывести уравнение геометрического места точек, сумма расстояний которых до двух данных точек F1(-c; 0), F2(c; 0) есть величина постоянная, равная 2а. Это геометрическое место называется эллипсом, точки F1 и F2 – фокусами эллипса. Доказать, что уравнение эллипса имеет вид  , где , где 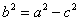 . .  |
| | | Вывести уравнение геометрического места точек, разность расстояний которых до двух данных точек F1(-c; 0), F2(c; 0) есть величина постоянная, равная 2а. Это геометрическое место называется гиперболой, точки F1 и F2 – фокусами гиперболы. Доказать, что уравнение гиперболы имеет вид 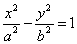 , где , где 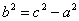 . .  |
| | | Вывести уравнение геометрического места точек, для которых расстояние до данной точки F(p/2; 0) равно расстоянию до данной прямой x=-p/2. Это геометрическое место называется параболой, точка F – фокусом параболы, данная прямая – ее директрисой. 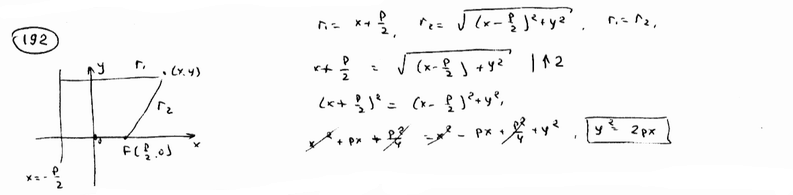 |
| | | Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки F(-4; 0) к расстоянию до данной прямой 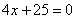 равно 4/5. равно 4/5. 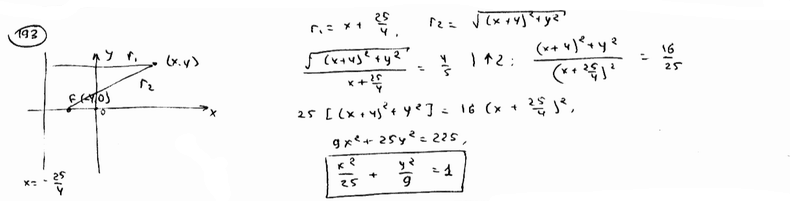 |
| | | Вывести уравнение геометрического места точек, для которых отношение расстояния до данной точки F(-5;0) к расстоянию до данной прямой 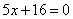 равно 5/4. равно 5/4. 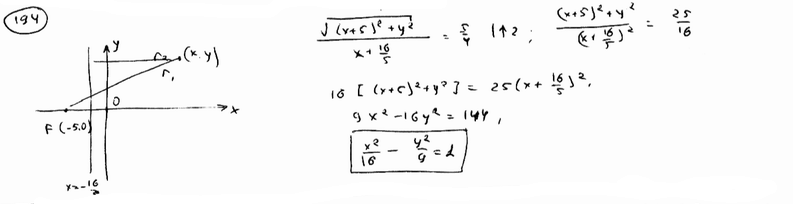 |
| | | Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей 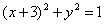 , , 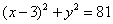 равны между собой. равны между собой.  |
| | | Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей 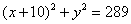 , , 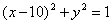 равны между собой. равны между собой. 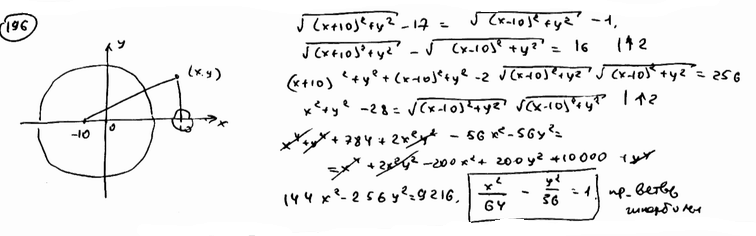 |
| | | Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до данной окружности 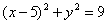 и до данной прямой и до данной прямой 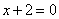 равны между собой. равны между собой. 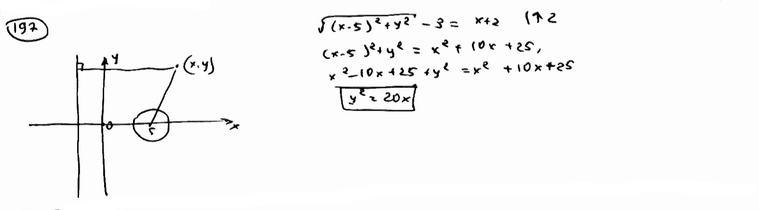 |
| | | Прямая перпендикулярна полярной оси и отсекает на ней отрезок, равный 3. Составить уравнение этой прямой в полярных координатах.  |
| | | Луч выходит из полюса и наклонен к полярной оси под углом 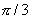 . Составить уравнение этого луча в полярных координатах. . Составить уравнение этого луча в полярных координатах.  |
| | | Прямая проходит через полюс и наклонена к полярной оси под углом 450. Составить уравнение этой прямой в полярных координатах.  |
| | | В полярных координатах составить уравнение геометрического места точек, расстояния которых от полярной оси равны 5. 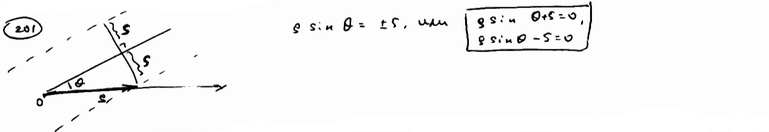 |
| | | Окружность радиуса R=5 проходит через полюс, ее центр лежит на полярной оси. Составить уравнение этой окружности в полярной системе координат. 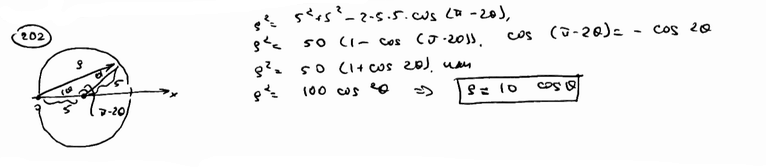 |
| | | Окружность радиуса R=3 касается полярной оси в полюсе. Составить уравнение этой окружности в полярной системе координат. 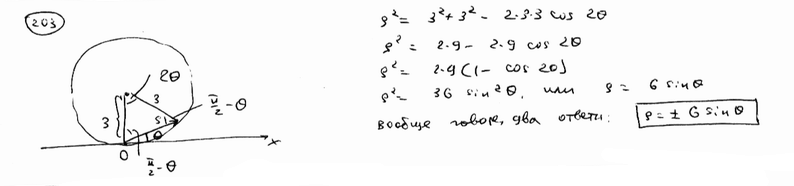 |



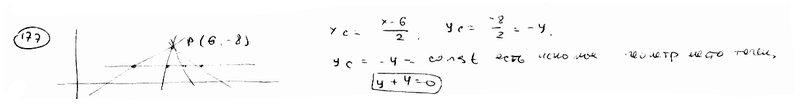
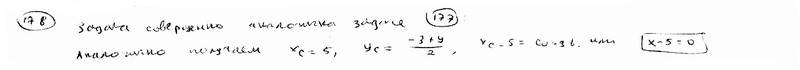

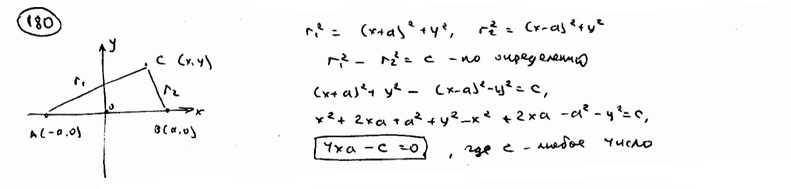

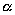 ;
; 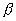 ) и радиус r.
) и радиус r. 
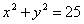 . Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8.
. Составить уравнение геометрического места середин тех хорд этой окружности, длина которых равна 8. 
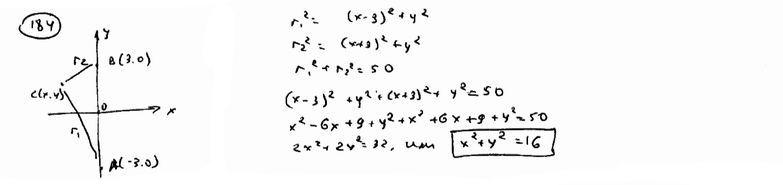
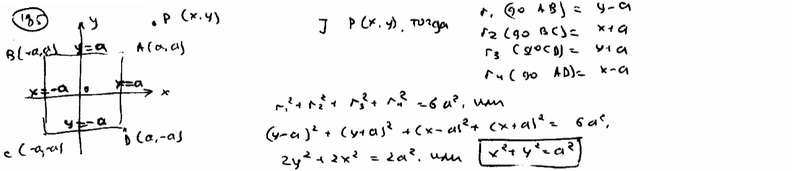
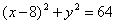 . Составить уравнение геометрического места середин этих хорд.
. Составить уравнение геометрического места середин этих хорд. 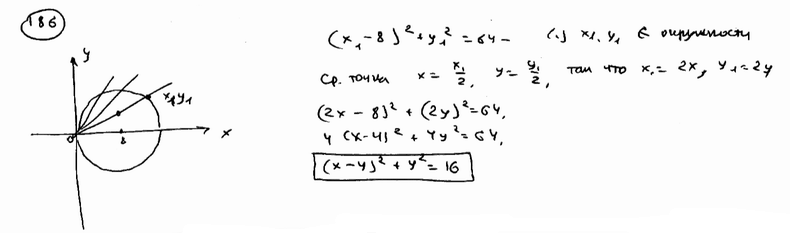
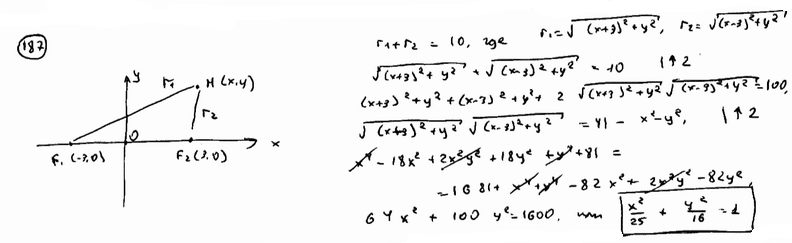
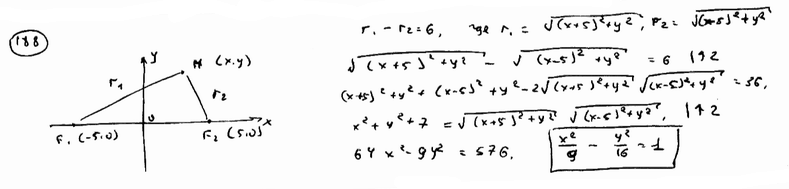
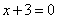 .
. 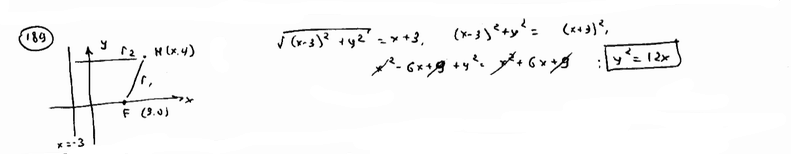
 , где
, где 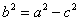 .
. 
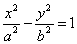 , где
, где 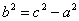 .
. 
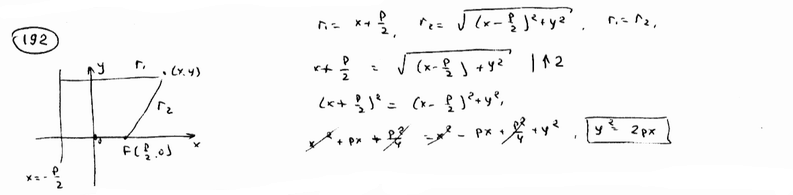
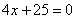 равно 4/5.
равно 4/5. 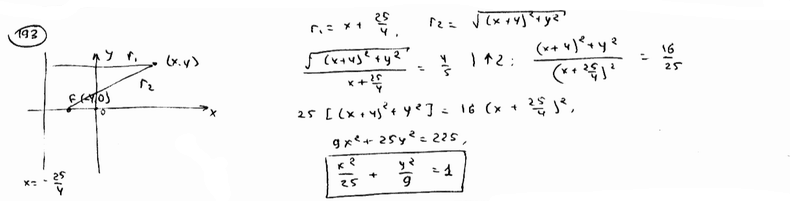
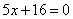 равно 5/4.
равно 5/4. 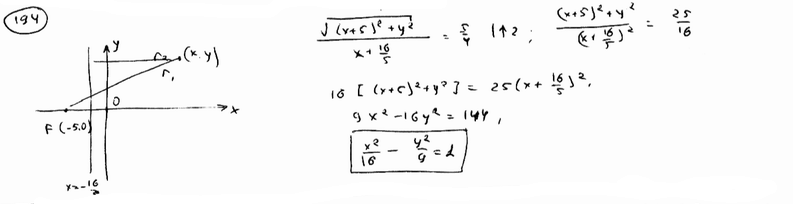
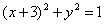 ,
, 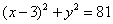 равны между собой.
равны между собой. 
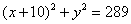 ,
, 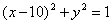 равны между собой.
равны между собой. 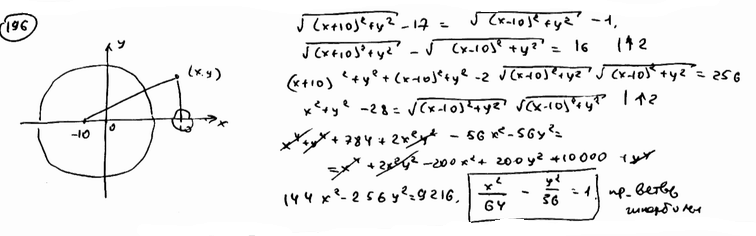
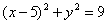 и до данной прямой
и до данной прямой 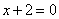 равны между собой.
равны между собой. 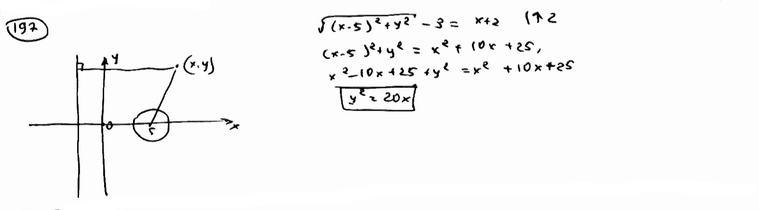

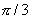 . Составить уравнение этого луча в полярных координатах.
. Составить уравнение этого луча в полярных координатах.