Признаки неизменяемости шарнирных систем

Равновесие плоской системы сил.

Для равновесия любой системы сил необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю, т.е. чтобы выполнялись условия: 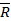=0, 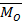=0, где О- любой центр.

Условия являются необходимыми, так как если какое-нибудь из них не выполняется, то система действующих на тело сил приводится или к равнодействующей (когда 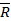≠0), или к паре сил (когда 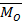≠0) и , следовательно, не является уравновешенной. Одновременно эти условия являются и достаточными, потому что при 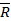=0система сил может приводится только к паре с моментом 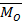, а так как 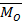=0, то имеет место равновесие.

На этом результате основана теорема Вариньона о моменте равнодействующей: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра О равен сумме моментов сил системы относительно того же центра.

На основании изложенного можно сформулировать аналитические условия равновесия плоской системы сил в трех различных формах:

1.Основная форма условий равновесия. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю. Одновременно это является условием равновесия твердого тела, находящегося под действием любой плоской системы сил.

2. Вторая форма условий равновесия.Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-нибудь центров А и В и сумма их проекций на ось Ох, не перпендикулярную прямой АВ, были равны нулю.

3. Третья форма условий равновесия.(уравнения трех моментов) Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых трех центров А, В и С не лежащих на одной прямой, были равны нулю.

Для получения более простых уравнений следует:

- составляя уравнения проекций, проводить координатную ось перпендикулярно какой-нибудь неизвестной силе;

- составляя уравнения моментов, брать центр моментов в точке, где пересекается большее количество неизвестных сил.

Признаки неизменяемости шарнирных систем.

Сооружение должно быть геометрически неизменяемым, т. е. постоянно сохранять геометрическую форму, заданную при возведении. Изменяемые системы недопустимы, так как они резко меняют форму, получая произвольные перемещения без изменения длин стержней. Неизменяемые же системы могут менять форму только в результате деформаций стержней. Примером простейшей неизменяемой системы является шарнирный треугольник, единственно возможный при заданных длинах стержней. Простейшей изменяемой системой является шарнирный четырехугольник, в котором перемещения узлов могут быть конечными без изменения длин стержней системы.

При расчете сооружений нередко используют основную схему в виде так называемой кинематической цепи — изменяемой системы. Важно знать степень свободы кинематической цепи и уметь перейти от этой цепи к неизменяемой системе путем ведения соответствующих связей.

Степенью свободы системы называется число независимых геометрических перемещений, определяющих ее положение (например, линейных перемещений узлов). Степень свободы шарнирного четырехугольника равна единице (достаточно поставить раскос по диагонали четырехугольника, чтобы обратить систему в неизменяемую).

Формула для определения числа связей плоской стержневой системы. Рассмотрим плоские шарнирно-стержневые системы стержней или дисков. Пусть задана шарнирно- стержневая система по рис. 1.3.1, в которой шесть шарнирных узлов связаны стержнями (ab,ac,ad….). Установим соотношение между числом узлов системы k и числом стержней s. Под k понимаем число узлов без опорных, а под s - число стержней вместе с опорными. При отсутствии всех s стержней системы степень свободы будет 2 k так как степень свободы каждого узла на плоскости равна двум.

При наличии связей числом s = 2 k система может быть неподвижна, если стержни расположены целесообразно. Условие неизменяемости системы будет

s = 2 k (1.3.1)

для системы по рис. 1.2.1. s = 12, k=6

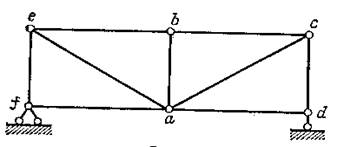
Рисунок 1.3.1.

Мы получили аналитический признак геометрической неизменяемости, согласно которому число связей между узлами равно возможной степени свободы узлов. Если s< 2k, система изменяема, она не имеет необходимого числа связей. Если s=2k , система обладает достаточным количеством связей для создания геометрически неизменяемой системы. Если же связи расположены нецелесообразно, система может оказаться изменяемой. Итак соотношение s=2k является необходимы, но недостаточным условием геометрической неизменяемости. То же можно сказать и относительно соотношения s>2k.

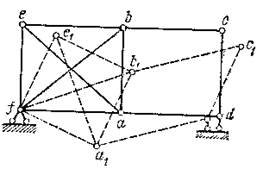
Рисунок 1.3.2.

В качестве примера приведем ферму в первой панели которой имеем два раскоса, а во второй раскоса нет (рис.1.3.2). Общее число стержней и узлов в данном случае s= 12; k= 6, т.е. s = 2k. Однако система изменяема, так как она сводится к шарнирному четырехугольнику (имеем диск abef, который заменяем одним стержнем).