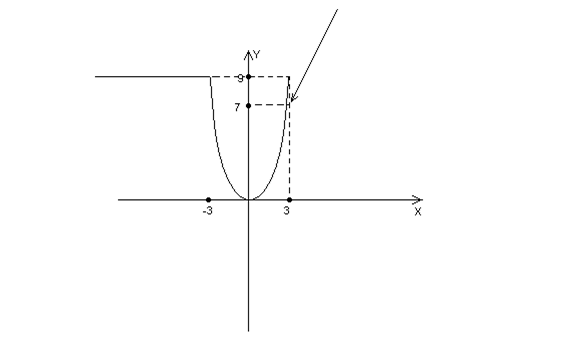Глава 3. Введение в анализ. Дифференциальное исчисление функции одной переменной
Теоретические вопросы
1. Понятие функции одной переменной.
2. Предел функции.
3. Непрерывность функции.
4. Бесконечно малые функции и их свойства.
5. Бесконечно большие функции и их свойства.
6. Односторонние пределы.
7. Производная функции.
8. Таблица производных.
9. Правила дифференцирования.
10. Производная сложной функции.
11. Производные высших порядков. Правило Лопиталя.
12. Исследование функций с помощью производных.
Литература
1. Н.С. Пискунов Дифференциальное и интегральное исчисления для втузов.- М.:Наука,1989,т.1,2.
2. В.С. Щипачев Высшая математика.- М.: Высшая школа, 1990.
3. П.Е. Данко, А.Г.Попов, Т.Я.Кожевникова Высшая математика в упражнениях и задачах.- М.: Высшая школа,1998,ч.1,2.
Предел функции
Пусть функция 
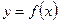 определена на множестве
определена на множестве 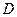 . Число А называется пределом функции
. Число А называется пределом функции 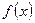 при
при 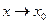 , если
, если 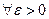
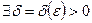 , что
, что 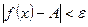 при
при 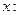
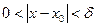 .
.
Это записывают так:
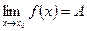 .
.
Если 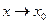 и
и 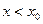 , то используют запись
, то используют запись 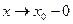 ; если
; если 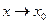 и
и 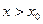 , то
, то 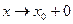 .
.
Числа 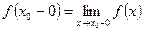 и
и 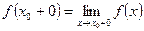 называются соответственно левосторонним и правосторонним пределами функции
называются соответственно левосторонним и правосторонним пределами функции 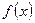 в точке
в точке 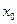 .
.
Если существуют пределы 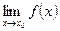 и
и 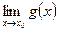 , то:
, то:
1) 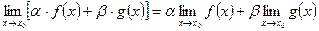 , где
, где 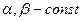 ;
;
2) 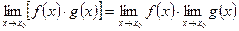 ;
;
3) 
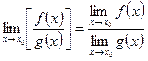
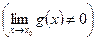 .
.
При решении задач полезно знать следующие “замечательные” пределы:
1) 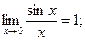 2)
2) 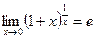 ; 3)
; 3) 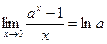 ; 4)
; 4) 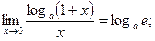
5) 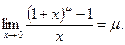
Нарушение ограничений, накладываемых на функции при вычислении их пределов, приводит к неопределенностям вида 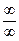 ,
, 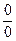 ,
, 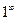 ,
, 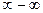 , и т.д.
, и т.д.
Существуют различные приемы раскрытия данных неопределенностей:
деление числителя и знаменателя на старшую степень переменной (при 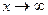 ); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т.п.
); сокращение на множитель, создающий неопределенность; применение “замечательных” пределов и т.п.
Задание 1. Найти пределы функций, не пользуясь правилом Лопиталя.
1) 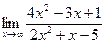
Решение. При 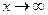 получаем неопределенность вида
получаем неопределенность вида 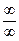 . Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на
. Чтобы найти предел данной дробно - рациональной функции, необходимо предварительно разделить числитель и знаменатель дроби на 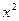 , т.к. степень
, т.к. степень 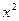 - наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
- наивысшая степень многочленов, определяющих данную рациональную функцию. Применяя основные теоремы о пределах и свойства бесконечно малых величин, получаем:
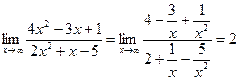
2) 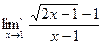
Решение. Непосредственная подстановка предельного значения аргумента 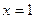 приводит к неопределенности вида
приводит к неопределенности вида 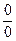 . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сумму 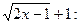
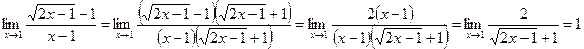
3) 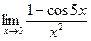
Решение Здесь имеет место неопределенность вида 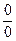 . Вычисление данного предела основано на применении первого “ замечательного” предела (
. Вычисление данного предела основано на применении первого “ замечательного” предела ( 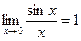 ).Имеем:
).Имеем: 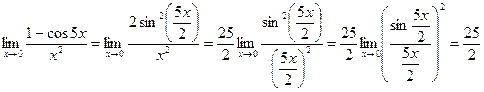
4) 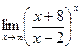
Решение. При 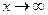 данная функция представляет собой степень, основание которой стремится к 1, а показатель – к
данная функция представляет собой степень, основание которой стремится к 1, а показатель – к 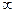 (неопределенность вида
(неопределенность вида 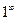 ). Преобразуем функцию так, чтобы использовать второй “замечательный” предел (
). Преобразуем функцию так, чтобы использовать второй “замечательный” предел ( 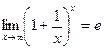 ). Получим:
). Получим:
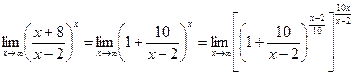 .
.
Так как 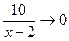 при
при 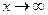 ,то
,то 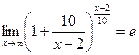 . Учитывая, что
. Учитывая, что 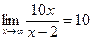 , находим
, находим 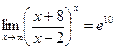 .
.
Непрерывность функции
Функция 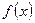 называется непрерывной в точке
называется непрерывной в точке 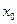 , если:
, если:
1) эта функция определена в некоторой окрестности точки 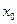
2) 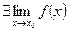
3) 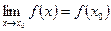 .
.
Теорема. Для того чтобы функция 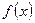 была непрерывна в точке
была непрерывна в точке 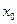 , необходимо и достаточно, чтобы выполнялись равенства:
, необходимо и достаточно, чтобы выполнялись равенства: 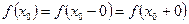 .
.
Точка 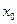 называется точкой разрыва непрерывности функции, если в этой точке функция не является непрерывной, т.е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.
называется точкой разрыва непрерывности функции, если в этой точке функция не является непрерывной, т.е. если в этой точке нарушается хотя бы одно из условий определения непрерывности функции.
Если существуют конечные односторонние пределы 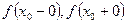 , причем не все три числа
, причем не все три числа 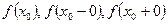 равны между собой, то
равны между собой, то 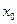 называется точкой разрыва первого рода. В частности, если:
называется точкой разрыва первого рода. В частности, если:
1) 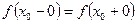 , то
, то 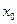 называется устранимой точкой разрыва;
называется устранимой точкой разрыва;
2) 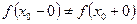 , то
, то 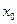 называется точкой разрыва типа скачка, причем разность
называется точкой разрыва типа скачка, причем разность 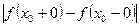 называется скачком функции
называется скачком функции 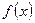 в точке
в точке 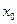 .
.
Точки разрыва функции, не являющиеся точками разрыва первого рода, называются точками разрыва второго рода.
Справедливо следующее утверждение.
Задание 2. Задана функция 
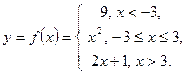
Исследовать функцию на непрерывность. Сделать чертеж.
Решение Функция 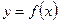 задана различными непрерывными аналитическими выражениями для различных областей изменения аргумента
задана различными непрерывными аналитическими выражениями для различных областей изменения аргумента 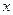 . Следовательно, точками разрыва данной функции могут быть только те точки, в которых меняются аналитические выражения функции, т.е. точки
. Следовательно, точками разрыва данной функции могут быть только те точки, в которых меняются аналитические выражения функции, т.е. точки 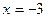 и
и 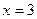 . Определим значения функции и ее односторонние пределы в этих точках:
. Определим значения функции и ее односторонние пределы в этих точках:
1) 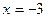 :
:
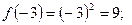
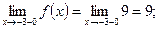
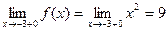 .
.
Так как 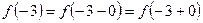 , то в точке
, то в точке 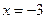 функция
функция 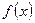 непрерывна.
непрерывна.
2) 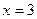 :
:
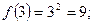
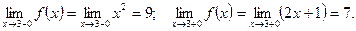
Так как 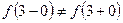 , то точка
, то точка 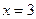 является точкой разрыва непрерывности функции
является точкой разрыва непрерывности функции 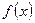 первого рода типа скачка.
первого рода типа скачка.
Скачок функции в точке разрыва равен: 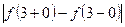 =2. График функции
=2. График функции 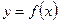 представлен на рисунке:
представлен на рисунке: