Теоретическое обоснование. Кручением называется такой вид деформации, при котором в любом поперечном сечении
Кручением называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент.
Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов. Крутящий момент в сечениях бруса определяется с помощью метода сечений (РОЗУ). Крутящий момент в каком-либо поперечном сечении вала численно равен алгебраической сумме внешних моментов, приложенных к брусу справа или слева от сечения
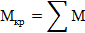
Знаки внешнего момента:
· вал рассматриваем слева направо – по часовой стрелке знак плюс, против - минус;
· вал рассматривается справа налево – знаки наоборот.
Прочность бруса, работающего на кручение, считают обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышает допускаемых
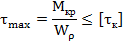
где 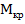 – момент крутящий, внутренний силовой фактор при деформации кручение; (Нм)
– момент крутящий, внутренний силовой фактор при деформации кручение; (Нм)
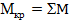
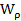 - полярный момент сопротивления, геометрическая характеристика прочности бруса круглого поперечного сечения при кручении;
- полярный момент сопротивления, геометрическая характеристика прочности бруса круглого поперечного сечения при кручении; 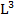
для круга 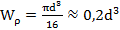
для кольца 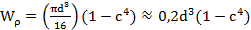
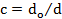
Три типа расчета на прочность:
1. Проверка прочности (проверочный расчет)
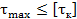
Незначительное превышение расчетного напряжения (до 5…6%) над допускаемым не опасно. Процент недогрузки может составлять 5-10%, т.е. 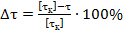
2. Подбор сечения (проектный расчет)
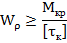
3. Определение допускаемого крутящего момента
(расчет допускаемой нагрузки)
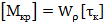
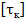 – допускаемое напряжение, МПа
– допускаемое напряжение, МПа
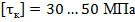
Кроме прочности к валам предъявляется требование жесткости. За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины) вала
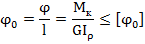 | 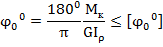 |
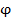 - полный угол закручивания, рад
- полный угол закручивания, рад
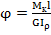
По условию жесткости выполняют три вида расчета:
1. Проверка прочности (проверочный расчет)
Условие жесткости бруса при кручении состоит в том, чтобы относительный угол закручивания 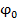 не превосходил некоторого заданного допускаемого значения
не превосходил некоторого заданного допускаемого значения 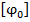 , т.е.
, т.е.
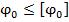
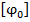 - допускаемый угол закручивания, зависит от назначения вала
- допускаемый угол закручивания, зависит от назначения вала
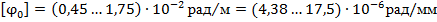
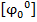 - допускаемый угол закручивания в градусах
- допускаемый угол закручивания в градусах
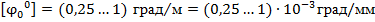
2. Подбор сечения (проектный расчет)
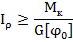
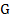 – модуль сдвига или модуль упругости второго рода, характеризует жесткость материала, МПа.
– модуль сдвига или модуль упругости второго рода, характеризует жесткость материала, МПа.
Между модулем упругости 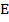 и модулем сдвига
и модулем сдвига 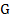 существует зависимость
существует зависимость
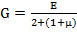
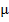 – коэффициент поперечной деформации, коэффициент Пуассона
– коэффициент поперечной деформации, коэффициент Пуассона
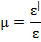
Далее, в зависимости от формы сечения (круг или кольцо)по найденному значению 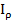 определяют диаметры
определяют диаметры
3. Определение допускаемого крутящего момента
(расчет допускаемой нагрузки)
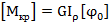
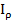 - полярный момент инерции - характеризует геометрию плоского сечения при деформации кручение, т.е. сопротивление сечения повороту вокруг полюса, начала координат. Единицы измерения
- полярный момент инерции - характеризует геометрию плоского сечения при деформации кручение, т.е. сопротивление сечения повороту вокруг полюса, начала координат. Единицы измерения 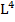
Осевые моменты инерции:
для круга 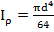
для кольца 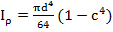
Для обеспечения прочности и жесткости одновременно из двух найденных значений выбираем большее. Полученное значение следует округлить, чтобы число заканчивалось на 5 или 0.
Алгоритм решения
Из условия прочности на кручение можно произвести три вида расчета.
1. Проверочный расчет выполняется в такой последовательности
· находим максимальный крутящий момент в поперечном сечении вала
· определяем полярный момент сопротивления сечения вала по формулам для круга и кольца
· находим максимальное расчетное касательное напряжение
· сравниваем расчетное напряжение с допускаемым
2. Расчет на определение допускаемой нагрузки вала выполняется в такой последовательности
· находим полярный момент сопротивления 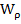
находим допускаемое значение крутящего момента
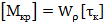
· находим допустимое значение приложенных к валу внешних (вращающих) моментов 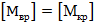
· из уравнения, выражающего зависимость между вращающим моментом, угловой скоростью и передаваемой мощностью, находим, какую максимальную мощность можно передать с помощью данного вала при заданной угловой скорости или наименьшую угловую скорость вала, при которой может передаться заданная мощность
3. Проектный расчет рекомендуется производить в такой последовательности
· находим крутящий момент в поперечном сечении вала
находим требуемую величину полярного момента сопротивления
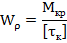
· Исходя из формы поперечного сечения (круг или кольцо) , по найденному значению 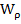 определяем величину диаметра вала; полученное значение округляем в сторону увеличения до ближайшего целого четного числи или числа, оканчивающегося на 5 или 10.
определяем величину диаметра вала; полученное значение округляем в сторону увеличения до ближайшего целого четного числи или числа, оканчивающегося на 5 или 10.
Из условия жесткости можно также производить три вида расчета.
1. Проверочный расчет
· найти максимальный крутящий момент
· определить полярный момент инерции
определить фактический относительный угол закручивания
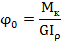
· сравнивая 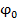 с
с 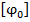 , определить, соблюдено или нет условие жесткости
, определить, соблюдено или нет условие жесткости
2. Последовательность расчета допускаемой нагрузки
· определить полярный момент инерции поперечного сечения вала
· полагая, что 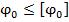 ,
,  из выражения условия жесткости определить допускаемый крутящий момент
из выражения условия жесткости определить допускаемый крутящий момент
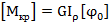
· по допустимому крутящему моменту найти допустимое значение приложенных к валу внешних скручивающих его моментов 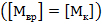
· из уравнения 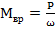 определить либо допускаемую мощность, которую можно передать при заданной угловой скорости, либо минимальную угловую скорость вала, при которой можно передать заданную мощность
определить либо допускаемую мощность, которую можно передать при заданной угловой скорости, либо минимальную угловую скорость вала, при которой можно передать заданную мощность
· если расчет допускаемой нагрузки выполняется из условия жесткости и из условия прочности, то из двух полученных допустимых значений 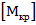 следует выбрать меньший
следует выбрать меньший
3. Последовательность проектного вала
· найти максимальный крутящий момент в поперечном сечении вала
· полагая в выражении условия жесткости 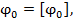
определить требуемую величину полярного момента
инерции
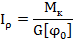
· исходя из формы поперечного сечения вала (круг или кольцо) по найденному значению 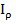 определить диаметр
определить диаметр
· если проектный расчет вала производится из условия жесткости и из условия прочности, то из двух вычисленных значений диаметра вала следует выбрать больший
ЗАДАНИЕ
ЗАДАЧА
Вариант А Задача 1.Из условия жесткости вала при 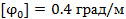 определить его диаметр, если вал должен передавать мощность определить его диаметр, если вал должен передавать мощность 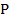 при угловой скорости при угловой скорости 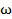 . Определив требуемый диаметр, найти наибольшие касательные напряжения, возникающие в поперечном сечении вала при его работе в заданном режиме. Задача 2.Определить диаметр стального вала для передачи мощности . Определив требуемый диаметр, найти наибольшие касательные напряжения, возникающие в поперечном сечении вала при его работе в заданном режиме. Задача 2.Определить диаметр стального вала для передачи мощности 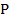 при угловой скорости при угловой скорости 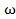 из условия прочности, приняв из условия прочности, приняв 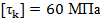 . Определив требуемый диаметр вала, найти угол его закручивания на длине . Определив требуемый диаметр вала, найти угол его закручивания на длине 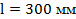 . Задача 3.При какой наименьшей угловой скорости стальной вал кольцевого сечения . Задача 3.При какой наименьшей угловой скорости стальной вал кольцевого сечения 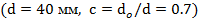 может передавать мощность может передавать мощность 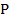 , чтобы максимальные касательные напряжения в поперечном сечении не превышали , чтобы максимальные касательные напряжения в поперечном сечении не превышали 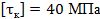 , относительный угол закручивания был бы не более , относительный угол закручивания был бы не более 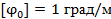 , , 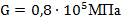 . Задача 4.Рассчитать наружный . Задача 4.Рассчитать наружный 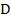 и внутренний и внутренний 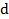 диаметры полого стального вала для передачи мощности диаметры полого стального вала для передачи мощности 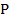 при угловой скорости при угловой скорости 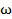 , приняв , приняв 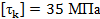 ; ; 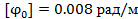 , , 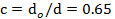 и и 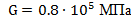 . Задача 5.Определить из условия жесткости диаметр стального вала . Задача 5.Определить из условия жесткости диаметр стального вала 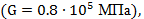 передающего мощность Р при угловой скорости передающего мощность Р при угловой скорости  , приняв , приняв 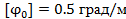 . Каким будет при этом коэффициент запаса вала по пределу текучести . Каким будет при этом коэффициент запаса вала по пределу текучести 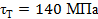 ? Задача 6.Для передачи какой мощности при угловой скорости ? Задача 6.Для передачи какой мощности при угловой скорости  рассчитан стальной вал диаметром рассчитан стальной вал диаметром 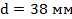 , если , если 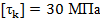 , , 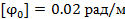 и и 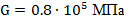 ? Задача 7.Сплошной вал, рассчитанный на передачу мощности Р при угловой скорости ? Задача 7.Сплошной вал, рассчитанный на передачу мощности Р при угловой скорости 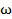 и и 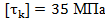 , решено заменить валом кольцевого сечения с отношением диаметров , решено заменить валом кольцевого сечения с отношением диаметров 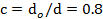 . Определить диаметры кольцевого сечения вала, не снижая его прочности по сравнению со сплошным валом. Во сколько раз вал кольцевого сечения будет легче сплошного? Задача 8.Сплошной вал, рассчитанный из условия жесткости при . Определить диаметры кольцевого сечения вала, не снижая его прочности по сравнению со сплошным валом. Во сколько раз вал кольцевого сечения будет легче сплошного? Задача 8.Сплошной вал, рассчитанный из условия жесткости при 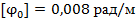 на передачу мощности на передачу мощности 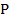 при угловой скорости при угловой скорости 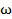 , решено заменить стальным валом кольцевого сечения с отношением диаметров , решено заменить стальным валом кольцевого сечения с отношением диаметров 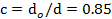 . Определить диаметры кольцевого сечения вала, не снижая его жесткости. Во сколько раз вал кольцевого сечения будет легче сплошного? Задача 9.Определить из условия прочности при . Определить диаметры кольцевого сечения вала, не снижая его жесткости. Во сколько раз вал кольцевого сечения будет легче сплошного? Задача 9.Определить из условия прочности при 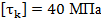 требуемый диаметр вала, передающего мощность требуемый диаметр вала, передающего мощность 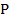 при угловой скорости при угловой скорости 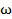 . Найти угол закручивания вала на длине . Найти угол закручивания вала на длине 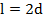 , где , где 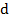 - принятый диаметр вала. Задача 10.Рассчитать из условия жесткости при - принятый диаметр вала. Задача 10.Рассчитать из условия жесткости при 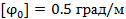 требуемый диаметр вала, передающего мощность требуемый диаметр вала, передающего мощность 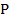 при угловой скорости при угловой скорости 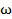 . Определить диаметр вала, найти коэффициент запаса по пределу текучести . Определить диаметр вала, найти коэффициент запаса по пределу текучести 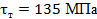 ; ; 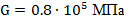 . . | Вариант Б Для данной схемы построить эпюру крутящих моментов; определить диаметр вала на каждом участке и полный угол закручивания. Указания: мощность на зубчатых колесах принять 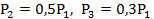 и и 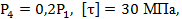 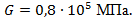 Полученное расчетное значение диаметра (мм) округлить до ближайшего большего числа, оканчивающегося на 0, 2, 5, 8 или по СТ СЭВ 208-75. Данные своего варианта принять по таблице Полученное расчетное значение диаметра (мм) округлить до ближайшего большего числа, оканчивающегося на 0, 2, 5, 8 или по СТ СЭВ 208-75. Данные своего варианта принять по таблице 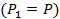 . . |
Примечание: для задач из варианта А принять по таблице мощность 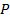 и угловую скорость
и угловую скорость 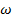 ; к задаче №3 дана только мощность, к задаче №6 - угловая скорость.
; к задаче №3 дана только мощность, к задаче №6 - угловая скорость.
| вар | № схемы | 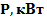 | 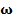 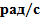 | Расстояние между шкивами, м | вар | № схемы | 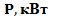 | 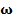 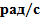 | Расстояние между шкивами, м | ||||
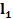 | 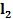 | 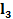 | 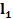 | 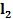 | 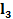 | ||||||||
| 0,1 | 0,2 | 0,5 | 0,2 | 0,7 | 0,6 | ||||||||
| 0,5 | 0,5 | 0,8 | 0,5 | 0,8 | 0,4 | ||||||||
| 0,2 | 0,9 | 0,4 | 0,6 | 0,9 | 0,5 | ||||||||
| 0,6 | 0,7 | 0,2 | 0,5 | 0,0 | 0,6 | ||||||||
| 0,2 | 0,5 | 0,5 | 0,8 | 0,2 | 0,4 | ||||||||
| 0,4 | 0,8 | 0,2 | 0,5 | 0,5 | 0,2 | ||||||||
| 0,2 | 0,5 | 0,8 | 0,8 | 0,8 | 0,6 | ||||||||
| 0,4 | 0,3 | 0,2 | 0,6 | 0,2 | 0,8 | ||||||||
| 0,8 | 0,4 | 0,6 | 0,4 | 0,6 | 0,5 | ||||||||
| 0,4 | 0,5 | 0,6 | 0,6 | 0,8 | 0,5 | ||||||||
| 0.4 | 0.8 | 0.3 | 0,1 | 0,9 | 0,4 | ||||||||
| 0.6 | 0.3 | 0.2 | 0,2 | 0,6 | 0,5 | ||||||||
| 0,8 | 0,2 | 0,5 | 0,9 | 0,8 | 0,3 | ||||||||
| 0,4 | 0,5 | 0,8 | 0,3 | 0,2 | 0,5 | ||||||||
| 0,2 | 0,8 | 0,2 | 0,4 | 0,5 | 0,3 | ||||||||
| 0,4 | 0,2 | 0,5 | 0,6 | 0,2 | 0,8 | ||||||||
| 0,6 | 0,5 | 0,8 | 0,4 | 0,9 | 0,5 | ||||||||
| 0,8 | 0,6 | 0,2 | 0,6 | 0,4 | 0,5 | ||||||||
| 1,0 | 0,6 | 0,5 | 0,1 | 0,5 | 0,4 | ||||||||
| 0,2 | 0,5 | 0,9 | 0,2 | 0,6 | 0,5 | ||||||||
| 0,4 | 0,2 | 0,6 | 0,9 | 0,8 | 0,3 | ||||||||
| 0,3 | 0,3 | 0,6 | 0,3 | 0,2 | 0,5 | ||||||||
| 0,6 | 0,4 | 0,8 | 0,4 | 0,5 | 0,9 | ||||||||
| 0,9 | 0,5 | 0,2 | 0,6 | 0,2 | 0,5 | ||||||||
| 0,3 | 0,6 | 0,5 | 0,5 | 0,5 | 0,8 |
| вар | № схемы | 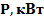 | 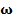 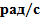 | Расстояние между шкивами, м | вар | № схемы | 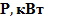 | 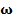 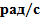 | Расстояние между шкивами, м | ||||
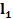 | 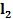 | 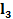 | 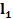 | 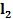 | 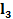 | ||||||||
| 1,0 | 0,4 | 0,5 | 0,2 | 0,5 | 0,5 | ||||||||
| 0,2 | 0,5 | 0,4 | 0,1 | 0,8 | 0,6 | ||||||||
| 0,4 | 0,8 | 0,3 | 0,8 | 0,5 | 0,2 | ||||||||
| 0,6 | 0,6 | 0,2 | 0,6 | 0,2 | 0,1 | ||||||||
| 0,8 | 0,2 | 0,5 | 0,4 | 0,0 | 0,3 | ||||||||
| 0,6 | 0,5 | 0,4 | 0,4 | 0,2 | 0,6 | ||||||||
| 0,2 | 0,8 | 0,2 | 0,3 | 0,3 | 0,6 | ||||||||
| 0,4 | 0,6 | 0,5 | 0,6 | 0,4 | 0,8 | ||||||||
| 0,6 | 0,5 | 0,8 | 0,9 | 0,5 | 0,6 | ||||||||
| 0,8 | 0,6 | 0,2 | 0,1 | 0,6 | 0,5 | ||||||||
| 0,1 | 0,6 | 0,5 | 0,2 | 0,7 | 0,6 | ||||||||
| 0,6 | 0,4 | 0,0 | 0,5 | 0,8 | 0,4 | ||||||||
| 0,5 | 0,8 | 0,2 | 0,0 | 0,9 | 0,5 | ||||||||
| 0,8 | 0,8 | 0,8 | 0,5 | 0,4 | 0,6 | ||||||||
| 0,6 | 0,6 | 0,4 | 0,3 | 0,2 | 0,2 | ||||||||
| 0,5 | 0,2 | 0,5 | 0,2 | 0,1 | 0,3 | ||||||||
| 0,8 | 0,1 | 0,6 | 0,3 | 0,2 | 0,1 | ||||||||
| 0,5 | 0,8 | 0,2 | 0,2 | 0,15 | 0,2 | ||||||||
| 0,2 | 0,6 | 0,1 | 0,1 | 0,3 | 0,25 | ||||||||
| 0,9 | 0,4 | 0,3 | 0,3 | 0,35 | 0,18 | ||||||||
| 0,0 | 0,1 | 0,5 | 0,25 | 0,15 | 0,1 | ||||||||
| 0,4 | 0,6 | 0,6 | 0,15 | 0,2 | 0,1 | ||||||||
| 0,8 | 0,5 | 0,2 | 0,1 | 0,15 | 0,3 | ||||||||
| 0,5 | 0,0 | 0,8 | 0,3 | 0,2 | 0,1 | ||||||||
| 0,0 | 0,6 | 0,4 | 0,25 | 0,15 | 0,1 |
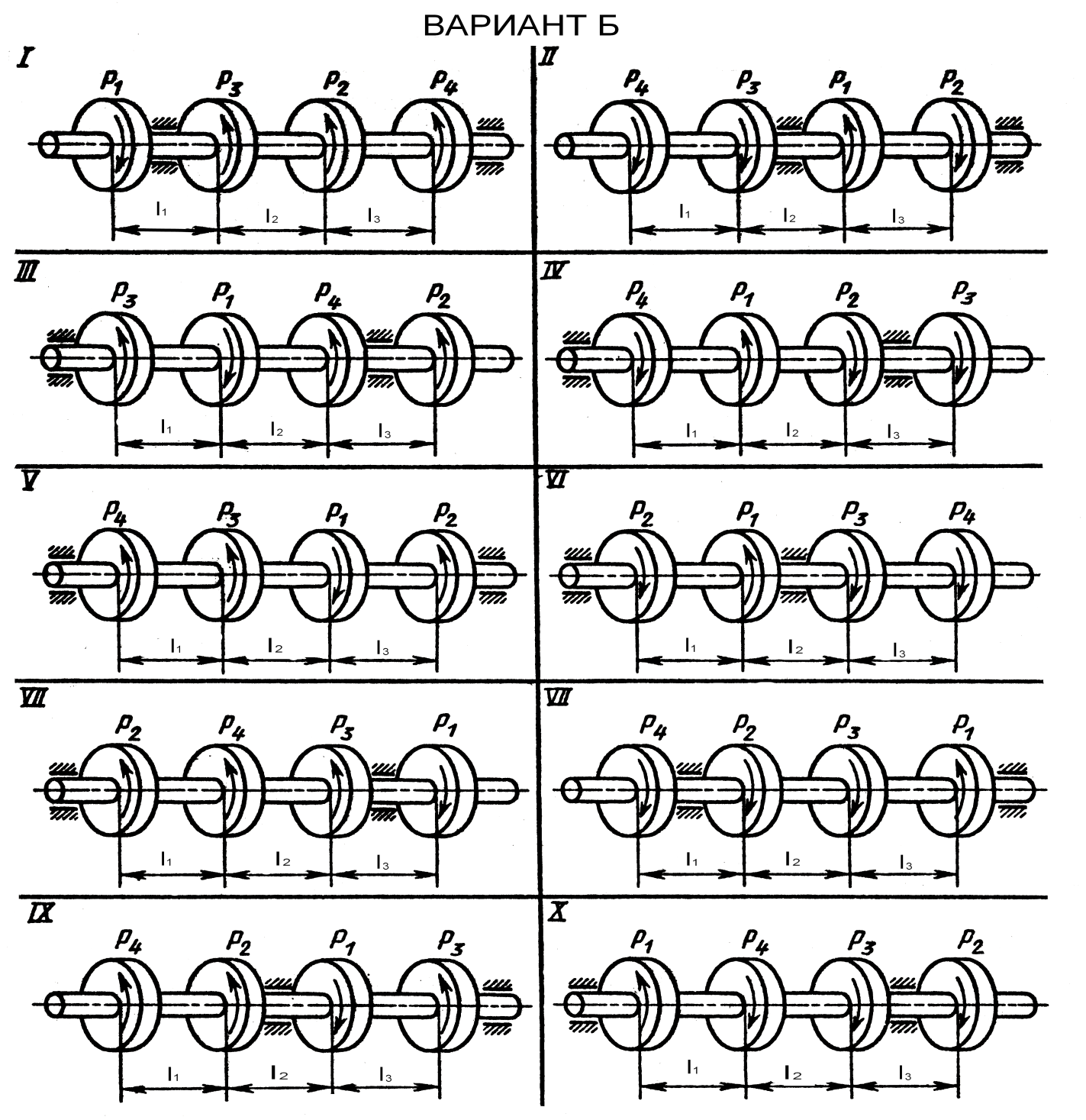
Пример выполнения
Задача
Для стального вала определить из условия прочности требуемые диаметры каждого участка и углы закручивания этих участков. Угловую скорость вала принять 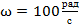 , допускаемое напряжение
, допускаемое напряжение 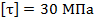 , модуль упругости сдвига
, модуль упругости сдвига 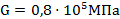 ,
, 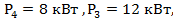
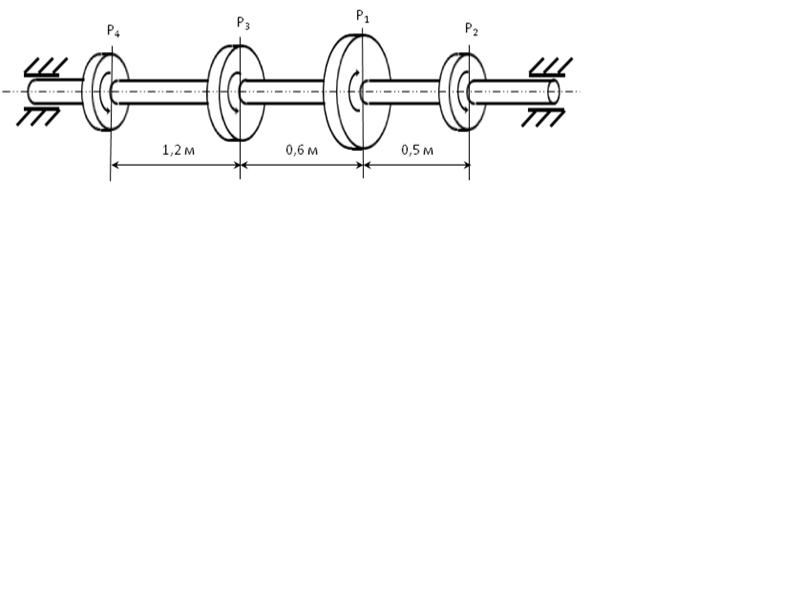
Решение.
1) Вал вращается с постоянной угловой скоростью, следовательно, система вращающихся моментов уравновешена. Мощность, подводимая к валу без учета потерь на трение, равна сумме мощностей снимаемых с вала:
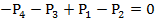
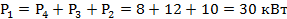
2) Определяем вращающий момент.
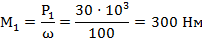
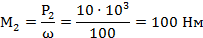
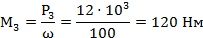
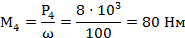
3)
Применяя метод сечений (РОЗУ) и определяем момент крутящий. Имеем три участка. Рассматриваем вал слева на право.
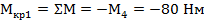 , на участке - CONST.
, на участке - CONST.
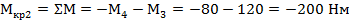 , на участке - CONST.
, на участке - CONST.
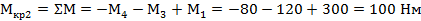 , на участке - CONST.
, на участке - CONST.
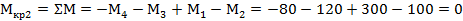 , на участке - CONST.
, на участке - CONST.
Для проверки рассмотрим вал справа на лево:
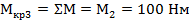
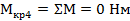
4)
Строим эпюру.
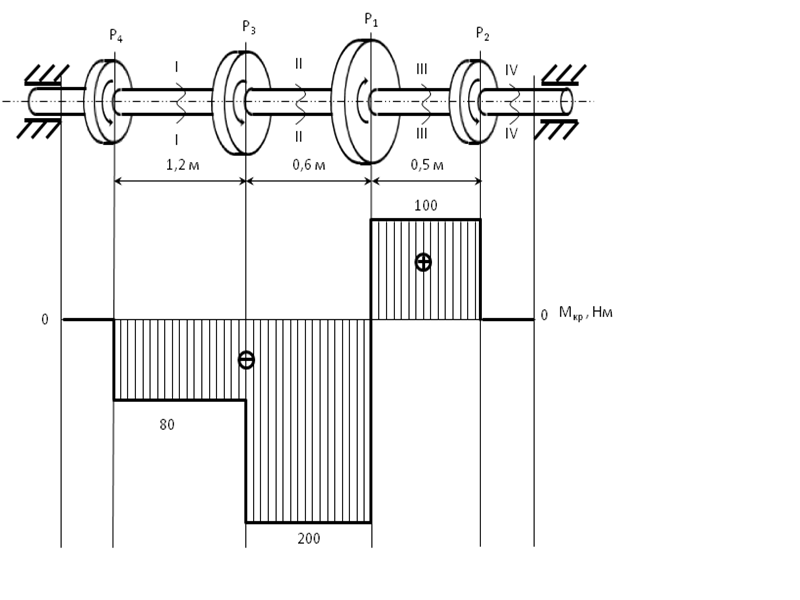
Масштаб 1см - 40 Нм
5)
Исходя из условия прочности при кручении:
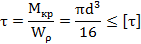
определяем диаметр:
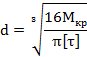
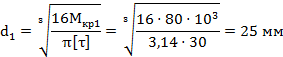
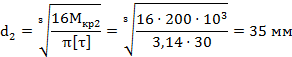
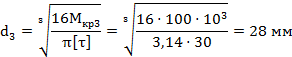
6)
Определяем полярный момент:
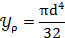
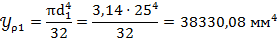
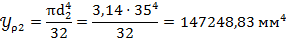
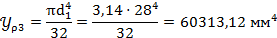
7)
Определяем угол закручивания:
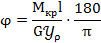
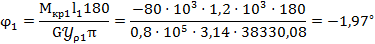
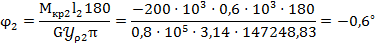
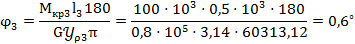
Контрольные вопросы.
1. Как нужно нагрузить брус, чтобы он работал только на кручение?
2. Каким образом определить в любом поперечном сечении бруса величину крутящего момента?
3. Сформулируйте правило знаков при определении величины крутящего момента
4. На каких гипотезах и допущениях основаны выводы расчетных зависимостей при кручении?
5. По какому закону распределяются напряжения в поперечном сечении круглого бруса?
6. Какой величиной характеризуется деформация при кручении?
7. Что такое полярный момент инерции поперечного сечения бруса?
8. Что такое жесткость сечения бруса?
9. Что такое полярный момент сопротивления? Как он определяется для круга и кольца?
10. Как определяется напряжение в любой точке круглого поперечного сечения бруса и как определяется наибольшее напряжение?
11. Запишите математическое условие прочности и жесткости при кручении. Сколько и какие расчеты можно производить из этого условия?
12. Справедлив ли закон Гука при кручении, если напряжение не превышает предела пропорциональности?
13. Зависят ли рабочие (расчетные) напряжения от материала вала?
14. Зависит ли угол поворота сечения вала от материала, из которого он изготовлен?
15. Во сколько раз уменьшится максимальное напряжение в поперечных сечениях вала, если его диаметр увеличить в два раза?
СР №14
