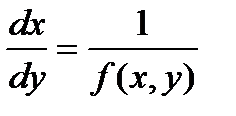Общие сведения о ДУ 1-го порядка
Раздел 11. Дифференциальные уравнения.
1. Общие сведения о ДУ 1-го порядка.
2. Уравнения с разделяющимися переменными.
3. Однородные ДУ 1-го порядка.
4. Линейные ДУ 1-го порядка.
5. ДУ в полных дифференциалах
6. Линейные ДУ II порядка.
7. Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами (ЛОДУ).
8. Линейные неоднородные ДУ 2-го порядка с постоянными коэффициентами (ЛНДУ).
Решение многих задач естествознания часто приводит к таким ситуациям, когда не удается сразу найти законы, связывающие непосредственно изучаемые величины. Вместе с тем, удается найти соотношения, связывающие используемые величины и их производные или дифференциалы. Такие соотношения называются дифференциальными уравнениями(ДУ).
При решении практических задач физики или геометрии составляют ДУ, описывающие исследуемое явление. При составлении ДУ обычно приходят к одному из следующих видов уравнений:
1) ДУ в производных
2) ДУ в дифференциалах
3) Простейшие интегральные уравнения с последующим преобразованием их в ДУ.
Общие сведения о ДУ 1-го порядка.
Рассмотрим задачу, приводящую к ДУ.
1. Найти уравнение кривой, зная, что отрезок оси Оу, который отсекается касательной в произвольной точке кривой, равен удвоенной ординате точки касательной.
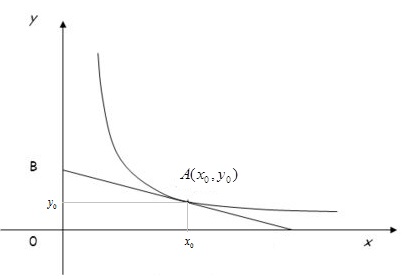
Возьмем кривую, заданную уравнением 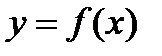 и возьмем произвольную точку
и возьмем произвольную точку 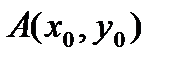 на этой кривой. Проведем касательную в этой точке, касательная пересекает ось ординат в точке
на этой кривой. Проведем касательную в этой точке, касательная пересекает ось ординат в точке 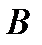 .
.
Отрезок 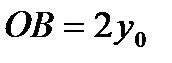 по условию, остается найти длину
по условию, остается найти длину  . Запишем уравнение касательной в точке
. Запишем уравнение касательной в точке  :
:
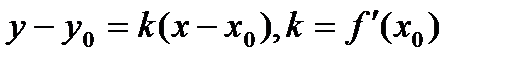
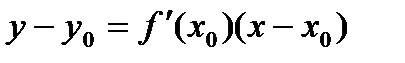
Найдем точку пересечения прямой с осью 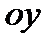 , т.е. с прямой
, т.е. с прямой 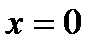 , подставим в уравнение касательной:
, подставим в уравнение касательной: 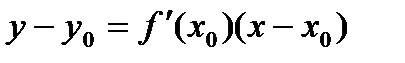
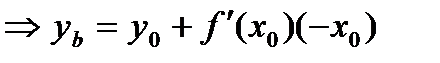
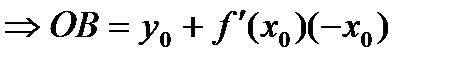
Используем условие 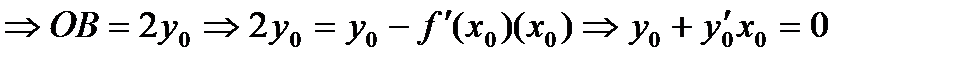
Получим равенство для точки 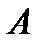 , и , поскольку точка
, и , поскольку точка 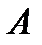 была любая на данной кривой, то это равенство справедливо для любой другой точки этой кривой , поэтому получаем следующее уравнение:
была любая на данной кривой, то это равенство справедливо для любой другой точки этой кривой , поэтому получаем следующее уравнение: 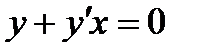 . В это уравнение входят: аргумент
. В это уравнение входят: аргумент 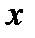 , неизвестная функция
, неизвестная функция 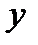 и ее производная. Решением этого уравнения будет
и ее производная. Решением этого уравнения будет 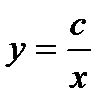 .
.
Рассмотрим основные определения.
Опр.1. Дифференциальным уравнением называется уравнение вида: 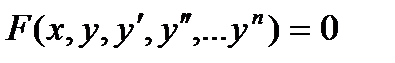 (1)
(1)
Опр. 2. Порядком ДУ называется порядок наивысшей производной, входящей в это уравнение, т.е. в уравнении (1) производная 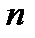 -ого порядка входит обязательно, остальные могут не входить. Например:
-ого порядка входит обязательно, остальные могут не входить. Например: 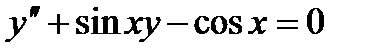 - ДУ 2-ого порядка.
- ДУ 2-ого порядка.
Опр.3. Если уравнение (1) можно записать в виде 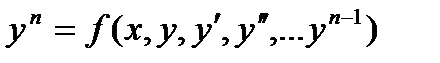 (2) ,
(2) ,
то оно называется ДУ, разрешенным, относительно старшей производной.
Опр.4. Решением ДУ (1) или (2) является функция 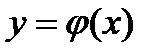 , которая обращает их в тождество:
, которая обращает их в тождество: 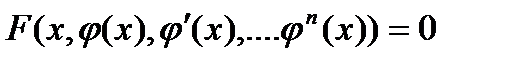
Например: функция 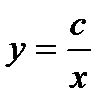 является решением ДУ
является решением ДУ 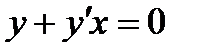 , т.к. при подстановке
, т.к. при подстановке 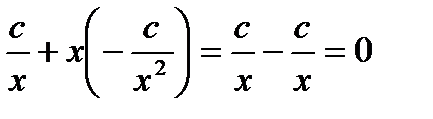
Этот пример показывает, что данное ДУ имеет не одно, а бесконечное множество решений 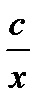 , где
, где  - любое число.
- любое число.
Пример: 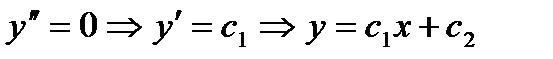 - прямая линия, т.е. решение этого уравнения 2-ого порядка зависит от 2-х произвольных постоянных.
- прямая линия, т.е. решение этого уравнения 2-ого порядка зависит от 2-х произвольных постоянных.
Оказывается, что в общем случае решение ДУ 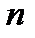 -ого порядка зависит от
-ого порядка зависит от 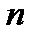 произвольных постоянных.
произвольных постоянных.
Опр.5. Функция 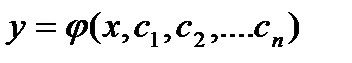 называется общим решением ДУ (1), если для любых значений параметров решение этого ДУ получается из общего при каких-то значениях произвольных постоянных
называется общим решением ДУ (1), если для любых значений параметров решение этого ДУ получается из общего при каких-то значениях произвольных постоянных 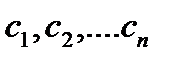 . Эти решения будем называть частными решениями ДУ.
. Эти решения будем называть частными решениями ДУ.
Теорема (о существовании и единственности решения ДУ).
Если в уравнении (2) функция 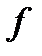 и ее частные производные по
и ее частные производные по 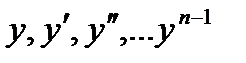 - непрерывны в некоторой области
- непрерывны в некоторой области 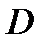 , содержащей точку
, содержащей точку 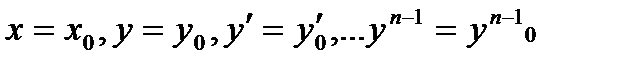 , то существует и единственное решение, удовлетворяющее следующим условиям:
, то существует и единственное решение, удовлетворяющее следующим условиям: 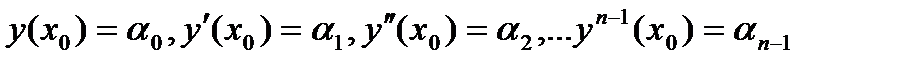 (3)
(3)
Условия (3) называются начальными условиями, а сама задача (2) с условиями (3), т.е. нахождение решения ДУ (2), удовлетворяющего начальным условиям(3), называется задачей Коши.
Обратимся к ДУ 1-ого порядка: 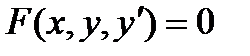 или
или 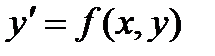 или
или 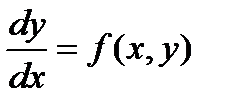 , с заданными начальными условиями
, с заданными начальными условиями 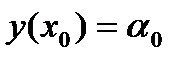 .
.
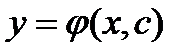 - общее решение ДУ.
- общее решение ДУ.
Будем рассматривать 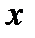 и
и 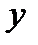 как координаты на плоскости, тогда решение представляет собой семейство интегральных кривых. Они сплошь заполняют всю плоскость, нигде не пересекаясь, и, если заданы начальные условия, то решить задачу Коши, означает выбрать из семейства интегральных кривых ту, которая проходит через точку
как координаты на плоскости, тогда решение представляет собой семейство интегральных кривых. Они сплошь заполняют всю плоскость, нигде не пересекаясь, и, если заданы начальные условия, то решить задачу Коши, означает выбрать из семейства интегральных кривых ту, которая проходит через точку 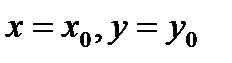 , т.е.
, т.е. 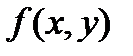 .
.
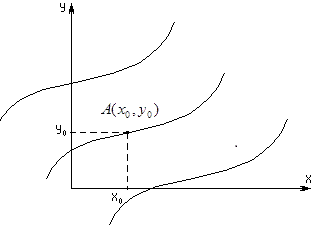
На практике и в теории необходимо иметь в виду возможность представления ДУ 1-ого порядка в виде