Экстремум функции нескольких переменных

9.1. Локальный экстремум

Пусть функция определена в некоторой –окрестности точки . Говорят, что функция имеет в точке локальный максимум (минимум), если существует такая – окрестность точки ; , что для любой точки выполняется неравенство

.

Локальный максимум и локальный минимум объединяются общим названием локальный экстремум.

9.2. Необходимое условие локального экстремума (теорема)

Если функция в точке имеет локальный экстремум и в этой точке существуют частные производные 1-го порядка по всем переменным, то все эти частные производные равны нулю: .

Если функция дифференцируема в точке , то соотношение также является необходимым условием локального экстремума.

Точки, в которых выполняются эти равенства, называются стационарными. Функция может принимать локальный экстремум только в стационарных точках или в точках, в которых частные производные первого порядка не существуют. Все такие точки называют критическими.

9.3. Знакоопределенные квадратичные формы

Функция переменных называется квадратичной формой. Числа – коэффициенты этой формы.

Квадратичная форма называется положительно (отрицательно) определенной, если для любых значений переменных , одновременно не равных нулю, она принимает положительные (отрицательные) значения.

Для того, чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы выполнялись неравенства

,

где

.

9.4. Достаточное условие локального экстремума

Пусть в некоторой окрестности стационарной точки функция 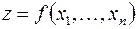дважды дифференцируемая и все частные производные второго порядка непрерывны в точке .

Если в этой точке второй дифференциал представляет собой знакоопределенную квадратичную форму от дифференциалов независимых переменных, то в точке функция имеет локальный экстремум. При этом если ( ) и , то в этой точке функция имеет локальный минимум (максимум). Этот случай соответствует условию: где .

Если в точке второй дифференциал представляет собой не строгую определенную квадратичную форму, т.е. или , что соответствует условию: или , и имеется , при котором , то требуется дальнейшее исследование и вопрос о существовании экстремума в точке решается с помощью приращений функции в окрестности критической точки.

Во всех остальных случаях в точке заведомо нет экстремума.

Пример. Исследовать на локальный экстремум функцию

Решение. Область определения данной функции – вся плоскость . Определим, в каких точках области определения данной функции выполняются необходимые условия существования экстремума.

Частные производные функции:

Для определения координат стационарных точек функции составляем систему уравнений

Отсюда и – точки возможного экстремума.

Проверим выполнение достаточных условий существования экстремума в точках знакоопределенности второго дифференциала

,

который представлен квадратичной формой от дифференциалов .

Вторые частные производные данной функции:

Рассмотрим точку . Поскольку , то – этот случай соответствует третьему условию. Следовательно, точка не является экстремальной.

В точке . Отсюда , т.е. выполняется первое условие. Следовательно, – точка минимума функции, причем

.

Пример. Исследовать на экстремум функцию

.

Решение. Необходимые условия существования экстремума выполняются в тех точках области определения данной функции, координаты которых удовлетворяют системе уравнений:

т.е.

Отсюда, геометрическое место критических точек есть прямая . Так как во всех точках прямой , то нужно исследовать функцию на экстремум, исходя из определения.

Определим знак приращения функции в точках найденной прямой:

Поскольку то .

Так как , то в точках прямой (а не в одной точке) функция имеет нестрогий минимум.

9.5. Условный экстремум

Функция имеет условный максимум (условный минимум) в точке , если существует такая окрестность точки , для всех точек которой , удовлетворяющих уравнениям связи

, где

выполняется неравенство

(соответственно ).

Задача нахождения условного экстремума сводится к исследованию не безусловный экстремум функции Лагранжа:

;

постоянные называются множителями Лагранжа.

При этом знак второго дифференциала в стационарной точке определяет характер экстремума при условии, что дифференциалы связаны соотношениями

,

где при .

Пример. Исследовать на экстремум функцию , если переменные связаны уравнением .

Решение. Графиком функции служит верхняя часть сферы. Эта функция имеет максимум в начале координат, ; если уравнение прямой есть , то геометрически ясно, что для точек этой прямой наибольшее значение функции достигается в точке , лежащей посередине между и . Точка – точка условного экстремума (максимума) функции на данной прямой, а ей соответствует точка на полусфере, аппликата которой .

Решим эту задачу через функцию Лагранжа

и исследуем ее на безусловный экстремум.

Стационарные точки функции определяются из системы уравнений

т.е. условный экстремум исследуемой функции совпадает с безусловным экстремумом функции .

Проверим выполнение достаточных условий существования экстремума в стационарной точке . С этой целью найдем вторые производные функции Лагранжа в стационарной точке .

;

;

,

откуда .

Так как при этом , то точка есть точка максимума функции , следовательно, точка условного максимума функции , причем .

9.6. Задачи на наибольшее и наименьшее значения функции

Если функция определена и непрерывна в некоторой ограниченной и замкнутой области и за исключением, быть может, отдельных точек имеет в этой области конечные частные производные, то в этой области найдется точка , в которой функция получает наибольшее и наименьшее из всех значений.

Для того, чтобы найти наибольшее или наименьшее значение функции в замкнутой области, нужно найти все максимумы или минимумы функции, достигаемые внутри этой области, а также наибольшее или наименьшее значение функции на границе области. Наибольшее из всех этих чисел и будет наибольшим значением, а наименьшее – наименьшим.

В задачах на отыскание наибольшего и наименьшего значений функции в замкнутой области приходится находить экстремальные значения функции на границе этой области, т.е. на некоторой линии, решая задачу исследования функции на условный экстремум.

Пример. Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной линиями .

Решение. Так как область задания функции замкнута и функция в ней непрерывна, то она обязательно принимает наибольшее и наименьшее значения в этой функции.

Исследуем функцию на экстремум внутри области задания функции.

Критические точки найдем, решая систему уравнений

Заметим, что только точка принадлежит области задания функции.

Проверим выполнение достаточных условий существования экстремума в точке :

;

;

.

Так как , то .

Исследуем функцию на границе области, которая состоит из отрезка оси , отрезка оси и отрезка прямой . На оси ; на оси . На отрезке прямой , уравнение которой , заданная функция пишется в виде функции одной переменной, например,

.

Исследуем эту функцию на наибольшее и наименьшее значения на отрезке . Эти значения существуют, так как непрерывна на указанном отрезке.

Необходимое существование экстремума этой функции выполняется при , так как .

Проверим выполнение достаточного условия существования экстремума функции в точке .

Так как , то при функция имеет минимум, .

Кроме того, на концах отрезка . Отсюда на

, .

Эти же значения являются наибольшими и наименьшими значениями функции 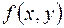на границе области задания.

Сравним значение функции с наибольшим и наименьшим значениями этой функции на границе области задания, делаем вывод: , .