Теорема о соотношении между сторонами треугольника. Неравенство треугольника

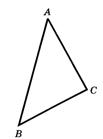Теорема. В треугольнике 1) против большей стороны лежит большой угол;

2) обратно, против большего угла лежит большая сторона.

Следствия: 1) В прямоугольном треугольнике гипотенуза больше катета.

2) Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника)

Теорема. Каждая сторона треугольника меньше суммы двух других сторон.

То есть для любых трех точек А, В, С не лежащих на одной прямой, справедливы неравенства: АВ<AC+CB, AC<AB+BC, BC<BA+AC. Каждое такое неравенство называется неравенством треугольника.

Запись на доске.

Теорема. 1)Если АВ>ВС, то ÐС>ÐА. 2) если ÐС>ÐА, то АВ>ВС

Следствия: 1) гипотенуза > катета.

2) Если ÐА = ÐВ, то ΔАВС - равнобедренный (признак равнобедренного треугольника)

Теорема. АВ<AC+CB, AC<AB+BC, BC<BA+AC

Задача.

Билет № 7

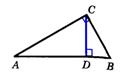
Теорема о пропорциональных отрезках в прямоугольном треугольнике.

Теорема. Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если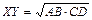

Из теоремы имеются следующие утверждения:

1°. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.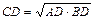

2°. Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. ,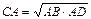

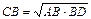
Следствия:1)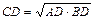

2) ,

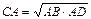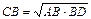
Смежные и вертикальные углы. Определение, свойство.

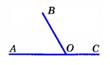Определение. Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными

На рисунке углы АОВ и ВОС смежные.

Свойство. Сумма смежных углов равна 180º.

Так как лучи ОА и ОС образуют развернутый угол, то АОВ+ ВОС= 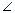АОС=180°.

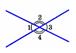Определение. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

На рисунке углы 1 и 3, а также 2 и 4 – вертикальные. Вертикальные углы обладают следующим свойством.

Свойство. Вертикальные углы равны.

Задача.

Билет № 8

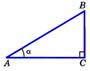1. Тригонометрические тождества. Доказательство основного тригонометрического тождества.

В курсе геометрии 8 класса изучается два тригонометрических тождества:

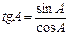и sin²A +cos²A=1 - основное тригонометрическое тождество.