Для самостоятельной работы студентов

Задание 1. Даны два неколлинеарных вектора Построить векторы:

1.1.	а)	б)	в)
1.2.	а)	б)	в)
1.3.	а)	б)	в)
1.4.	а)	б)	в)
1.5.	а)	б)	в)
1.6.	а)	б)	в)
1.7.	а)	б)	в)
1.8.	а)	б)	в)
1.9.	а)	б)	в)
1.10.	а)	б)	в)
1.11.	а)	б)	в)
1.12.	а)	б)	в)
1.13.	а)	б)	в)
1.14.	а)	б)	в)
1.15.	а)	б)	в)
1.16.	а)	б)	в)
1.17.	а)	б)	в)
1.18.	а)	б)	в)
1.19.	а)	б)	в)
1.20.	а)	б)	в)
1.21.	а)	б)	в)
1.22.	а)	б)	в)
1.23.	а)	б)	в)
1.24.	а)	б)	в)
1.25.	а)	б)	в)
1.26.	а)	б)	в)
1.27.	а)	б)	в)
1.28.	а)	б)	в)
1.29.	а)	б)	в)
1.30.	а)	б)	в)

Задание2.Найти длину вектора и его направляющие косинусы.

2.1.	А(1;2;0), В(3;0;3).	2.6.	А(0;6;4), В(3;5;3).
2.2.	А(3;0;1), В(–1;2;0).	2.7.	А(3;–1;2), В(1;2;–1).
2.3.	А(1;3;–1), В(1;–1;3).	2.8.	А(1;2;–1), В(–1;1;–3).
2.4.	А(3;1;4), В(–1;6;1).	2.9.	А(2;1;–1), В(3;0;1).
2.5.	А(2;–1;2), В(1;2;–1).	2.10.	А(3;–4;2), В(4;–2;0).

2.11.Доказатьколлинеарность векторов и . Установить, какой из них длиннее и во сколько раз и как они относительно друг друга направлены.

2.12. Определить, при каких значениях l и b векторы и коллинеарны.

2.13. Найти орт вектора .

2.14. Дан вектор . Найти вектор , противоположно направленный к вектору , если .

2.15. Найти длины диагоналей параллелограмма, построенного на векторах , .

2.16. Векторы и являются сторонами ∆АВС. Определить координаты векторов, проведенных из вершин треугольника и совпадающих с его медианами .

2.17. В точке А(1; 3) приложена сила, проекции которой на оси координат равны:х = 3, у = 4. Определить конец вектора 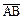, изображающего силу и величину силы.

2.18. Даны три вершиныпараллелограмма: А(3;–4; 7), В(–5; 3; –2), С(1; 2; –3). Найти его четвертую вершину D, противоположную вершине В.

2.19. Доказать, что точки А(3; –1; 2),В(–1; 1; –3), С(1; 2; –1),D(3; –5; 3) являются вершинами трапеции. Найти длины ее параллельных сторон.

2.20. В точке А(–3; –2) приложена сила, проекция которой у = –1, а проекция х положительна. Определить конец вектора , изобра­жающего силу, если его величина равна .

2.21. Найти единичный вектор, перпендикулярный вектору и оси Оу.

2.22. Найти вектор , коллинеарный вектору и удовлетворяющий условию .

2.23. Найти направляющие косинусы вектора, перпендикулярного к оси Оz и к вектору 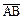, проходящему через точки А(1;–1;4) и В(–3;2;4).

2.24. Вектор , перпендикулярный к оси Oz и к вектору , образует острый угол с осью Оx. Зная, что длина вектора , найти его координаты.

2.25. Дан равносторонний треугольник АВС, у которого длины сторон равны 1. Полагая, что , , ,вычислить выра­жение .

2.26. Найти единичный вектор, перпендикулярный к векторам и .

2.27. Даны силы , , , прило­женные к одной точке. Вычислить работу равнодействующей этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из точки В(5; 3; –7) в точку С(4; –1; –4).

2.28. На материальную точку действуют силы , , . Найти работу равнодействующей этих сил при перемещении из точки В(–2; 5;–1) в точку С(0; 0; –3).

2.29. Упростить выражение , если , , , где , , .

2.30. Определить, при каком значении l векторы и будут взаимно перпендикулярны, если , , .

Задание 3. Разложить аналитически и геометрически вектор по векторам

3.1.		3.16.
3.2.		3.17.
3.3.		3.18.
3.4.	,	3.19.
3.5.	, ,	3.20.
3.6.	,	3.21.
3.7.	,	3.22.
3.8.	.	3.23.
3.9.	,	3.24.
3.10.		3.25.
3.11.		3.26.
3.12.		3.27.
3.13.		3.28.
3.14.		3.29.
3.15.		3.30.

Задание 4.Вычислить длины векторов угол между ними и проекцию .

4.1. .

4.2. .

4.3. .

4.4. .

4.5. .

4.6. .

4.7. .

4.8. .

4.9. .

4.10. .

4.11. Вычислить длины диагоналей параллелограмма, построенного на векторах и , если , и угол между ними .

4.12. Вычислить длины диагоналей параллелограмма, построенного на векторах и , где и – единичные векторы, угол между которыми 60^о.

4.13. Доказать, что вектор перпендикулярен к вектору .

4.14. Доказать, что вектор перпендикулярен к вектору .

4.15. Доказать, что скалярное произведение двух векторов не изменится, если к одному из них прибавить вектор, ортогональный к другому сомножителю.

4.16. Вычислить, какую работу производит сила , когда точка ее приложения перемещается прямолинейно из точки А(2;–3; 5) в точку В(3; –2; –1).

4.17. Силы , , приложены к одной точке. Вычислить величину и направляющие косинусы равнодействующей.

4.18. Найти единичный вектор, перпендикулярный к вектору и к оси Ох.

4.19. Найти вектор , коллинеарный вектору и удовлетворяющий условию .

4.20. В плоскости хОу найти вектор , перпендикулярный к вектору ,имеющий одинаковую с ним длину.

4.21. На плоскости хОу построить радиус-векторы , и . Разложить геометрически и аналитически вектор по векторам .

4.22. Разложить вектор по векторам и аналитически и геометрически.

4.23. Разложить вектор по векторам и аналитически и геометрически.

4.24. Вектор разложить по векторам и аналитически и геометрически.

4.25. Найти разложение вектора по векторам и аналитичес­ки и геометрически: , , .

4.26. Разложить вектор по векторам и аналитически и геометрически: , , .

4.27. Разложить вектор по векторам и аналитически и гео­метрически: , , . Будут ли векторы линейно зависимы?

4.28. , , .

4.29. , , .

4.30. , , .

Задание5.Сила приложена к вершине А треугольника АВС. Вычислить работу силы по сторонам АВ и АС, момент силы относительно середины стороны ВС.

5.1.	А(1; –2; 3);	В(0; –1; 2);	С(2; –3; 6);	(1; 0; 3).
5.2.	А(6; 0; –5);	В(3; 4; 1);	С(1; –2; 1);	(2; 3; 7).
5.3.	А(2; –1; 5);	В(7; 2; 1);	С(3; 0; 1);	(8; 0; 1).
5.4.	А(0; 3; –5);	В(7; 8; –4);	С(1; 2; –2);	(5; –1; 2).
5.5.	А(–1; 3; 0);	В(6; 5; –2);	С(0; 1; 2);	(2; 1; 3).
5.6.	А(5; 2; –1);	В(3; 0; 4);	С(1; 2; –2);	(1; 3; –5).
5.7.	А(3; 1; 4);	В(–2; 4; 6);	С(6; 0; 10);	(1; 4; 0).
5.8.	А(6; 2; 0);	В(–4; 10; 5);	С(–2; 6; 9);	(3; 2; 4).
5.9.	А(3; 2; –1);	В(5; 3; 3);	С(1; 10; 5);	(5; 1; 2).
5.10.	А(2; 0; 8);	В(4; 5; –2);	С(6; 3; 0);	(1; 7; –3).

Вычислить площадь треугольника АВС; длину высоты, про­веденной из вершины В; угол ВАС; .

5.11.	А(3;2;1);	B(6;2;5);	C(–1;2;1).
5.12.	A(1;3;–1);	B(2;0;4);	C(1;5;–2).
5.13.	A(2;0;3);	B(1;1;2);	C(3;1;4).
5.14.	A(1;2;3);	B(2;1;–3);	C(3;0;4).
5.15.	A(1;–2;0);	B(5;4;1);	C(1;–1;–1).
5.16.	A(0;1;2);	C(–1;3;2);	C(3;3;1).
5.17.	A(2;1;3);	B(–1;2;0);	C(3;2;5).
5.18.	A(5;3;2);	B(4;1;0);	C(8;4;3).
5.19.	A(2;0;–1);	B(3;4;–1);	C(2;1;0).
5.20.	A(5;–2;1);	B(2;–1;6);	C(6;1;3).

Диагонали параллелограмма лежат на векторах и . Вычислить площадь и меньшую высоту параллелограмма.

5.21.	3, 1, .	5.26.	4, 4, .
5.22.		5.27.	7, 7, .
5.23.		5.28.
5.24.	7, 2, .	5.29.
5.25.	1, 3, .	5.30.

Задание6.Проверить, лежат ли точки А, В, С, D в одной плоскос­ти?

6.1.	А(1;–2;3),	В(1;0;–1),	С(3;2;4),	D(0; –2; 1).
6.2.	А(3;0;–1),	В(2;1;4),	С(5;2;–2),	D(–1; –4; 1).
6.3.	А(2;1;–5),	В(3;0;1),	С(–2;7;1),	D(4; 3; 1).
6.4.	А(5;1;–1),	В(4;1;2),	С(0;3;–5),	D(3; 2; 1).
6.5.	А(6;3;–2),	В(0;2;5),	С(3;4;1),	D(0; 5; 4).
6.6.	А(1;5;2),	В(–3;1;1),	С(7;9;0),	D(1; 2; –3).
6.7.	А(4;2;–1),	В(3;1;6),	С(–2;5;–4),	D(8; 0; 1).
6.8.	А(2;1;5),	В(0;11;2),	С(3;8;1),	D(6; 2; 7).
6.9.	А(3;2;1),	В(–1;2;0),	С(3;5;–2),	D(11; 2; 3).
6.10.	А(2;6;3),	В(0; –3;5),	С(7; 2;–1),	D(–3; 10; 7).

Вершины тетраэдра расположены в точках А, В, С, D. Вычислить его объем и высоту, опущенную из вершины А на грань ВСD.

6.11.	А(–1; 0; 5),	В(1; 2; –1),	С(0; 2; 2),	D(–1;0;2).
6.12.	А(–5; 4; 8),	В(2; 3; 1),	С(4; 1; –2),	D(6;3;7).
6.13.	А(2; –4; 5),	В(–1; 3; 4),	С(5; 5; –1),	D(1;–2;2).
6.14.	А(0; 0; 0),	В(3; 4; –1),	С(2;3; 5),	D(6;0;–3).
6.15.	А(3; 2; –6),	В(4; –1; 3),	С(–2; 1; 0),	D(0;–5;1).
6.16.	А(3; 4; 5),	В(–1; 2; –3),	С(4; –1; 0),	D(2;1;–2).
6.17.	А(7; 5; –3),	В(2; 3; 1),	С(4; 1; –2),	D(6;3;7).
6.18.	А(–4; 3; –12),	В(1; 5; –7),	С(–3; 6; 3),	D(–2;7;3).
6.19.	А(8; 4; –9),	В(1; 2; 0),	С(3; 0; –3),	D(5;2;6).
6.20.	А(–1; 0; –2),	В(1; 1; 2),	С(–1; 1; 3),	D(2;–2;4).

Вычислить объем параллелепипеда, построенного на векторах , , , и его высоту, опущенную на грань, лежащую на векторах , .

6.21.	,	,	.
6.22.	,	,	.
6.23.	,	,	.
6.24.	,	,	.
6.25.	,	,	.
6.26.	,	,	.
6.27.	,	,	.
6.28.	,	,	.
6.29.	,	,	.
6.30.	,	,	.

ТЕСТОВЫе ЗАДАНИя

Задание 1.Ответить на вопрос задания, выбрав один из вариантов ответов.

Задание оценивается в 1 балл.