Решение однородных дифференциальных уравнений
Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.
Дифференциальное уравнение вида
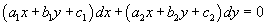
преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:
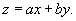
1.Решить дифференциальное уравнение 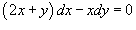 .
.
Решение.
Нетрудно заметить, что многочлены P(x,y) и Q(x,y), соответственно, при dx и dy, являются однородными функциями первого порядка. Поэтому, данное дифференциальное уравнение также будет однородным.
Положим y = ux, где u − некоторая новая функция, зависящая от x. Тогда
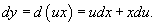
Подставляя это в дифференциальное уравнение, получаем
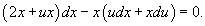
Следовательно,
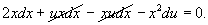
Разделим обе части уравнения на x:
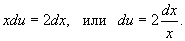
Выполняя деление x, мы могли потерять решение x = 0. Прямая подстановка показывает, что x = 0действительно является одним из решений нашего уравнения.
Интегрируем последнее выражение:
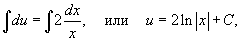
где C − постоянная интегрирования.
Возвращаясь к старой переменной y, можно записать:
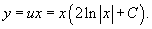
Таким образом, уравнение имеет два решения:
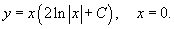
2.Решить дифференциальное уравнение 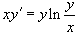 .
.
Решение.
Заметим, что корень x = 0 не принадлежит области определения заданного дифференциального уравнения. Перепишем уравнение в следующей форме:
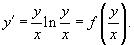
Как видно, уравнение является однородным.
Сделаем замену y = ux. Следовательно,
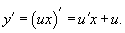
Подставляем полученное выражение в дифференциальное уравнение:

Разделим обе части на x ≠ 0:
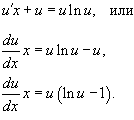
В результате мы получаем уравнение с разделяющимися переменными:
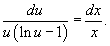
На следующем шаге проинтегрируем левую и правую части уравнения:
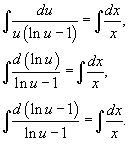
Следовательно,
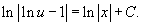
Постоянную C здесь можно записать как ln C1 (C1 > 0). Тогда

Если C1 = 0, то ответом является функция y = xe. Легко убедиться, что эта функция будет также и решением дифференциального уравнения. В самом деле, подставляя

в дифференциальное уравнение, находим:

Таким образом, все решения дифференциального уравнения можно представить одной формулой:
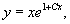
где C − произвольное действительное число.
3.Решить дифференциальное уравнение 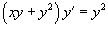 .
.
Решение.
Здесь мы снова встречаемся с однородным уравнением. В самом деле, запишем его в виде:
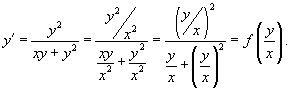
Сделаем подстановку y = ux. Тогда y' = u'x + u. Подставляя y и y' в исходное уравнение, получаем:
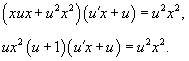
Разделим обе части уравнения на ux2. Заметим, что корень x =0 не является решением, но можно убедиться, что корень u = 0 (или y = 0) будет одним из решений данного дифференциального уравнения.
В результате получаем:
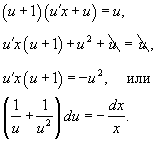
Интегрируя, находим общее решение:
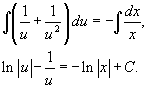
Учитывая, что 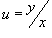 , последнее выражение можно записать в форме
, последнее выражение можно записать в форме
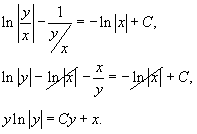
Обратная функция x(y) имеет явный вид:
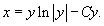
Поскольку C − произвольное число, знак "минус" перед этой константой можно заменить на знак "плюс". Тогда получаем:
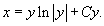
Таким образом, дифференциальное уравнение имеет решения:
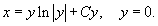
4.Решить дифференциальное уравнение  .
.
Решение.
Из вида правой части уравнения следует, что x ≠ 0 и y ≠ 0. Можно сделать подстановку: y = ux, y' = u'x + u, которая приводит к уравнению с разделяющимися переменными:

Интегрируя данное уравнение, получаем:
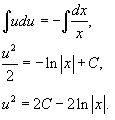
Переобозначим 2C просто как постоянную C. Следовательно,
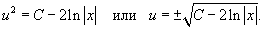
Итак, общее решение записывается в виде:
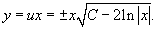
5.Найти общее решение дифференциального уравнения 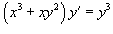 .
.
Решение.
Как видно, данное уравнение является однородным. Поэтому, воспользуемся подстановкой y = ux,y' = u'x + u. В результате уравнение преобразуется в уравнение с разделяющимися переменными:
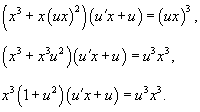
Разделим обе части на x3. (Заметим, что корень x = 0 не является решением).

Теперь можно проинтегрировать последнее уравнение:
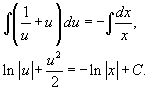
Так как u = y/x, то решение записывается в виде:
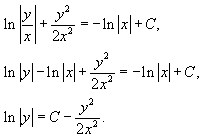
Отсюда следует, что
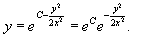
Переобозначим для краткости: eC = C1, (C1 > 0). Тогда решение в неявной форме определяется уравнением:
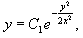
где постоянная C1 > 0.
