Множества точек, задаваемые алгебраическими уравнениями и неравенствами

Числовые множества

Множества могут состоять из объектов самой различной природы. Их элементами могут быть буквы, атомы, книги, люди и т.д. Для математики особо важную роль играют множества, составленные из “математических” объектов – чисел, точек, геометрических фигур и т.п. Примерами числовых множеств являются:

а) множество всех действительных чисел R;

б) множество всех рациональных чисел Q;

в) множество всех натуральных чисел N;

г) множество всех чисел вида 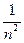, где n принимает все натуральные значения.

В предлагаемой лекции мы рассмотрим примеры числовых множеств специального вида.

Множества точек на прямой

Числовые промежутки

Пример, имеющий важные применения, – соответствие между множеством действительных чисел R и множеством точек числовой прямой, т.е. прямой, на которой выбраны начало отсчета (ему сопоставлено число 0) и масштаб, однозначно определяющий равномерную шкалу. Каждой точке прямой соответствует ровно одно действительное число – координата этой точки, и обратно, каждому действительному числу x сопоставляется точка прямой с координатой x. Точка, соответствующая большему числу, находится правее, меньшему числу – левее. Данное соответствие позволяет множество чисел интерпретировать на геометрическом языке как множество точек прямой.

Интервалы

Открытым интерваломназывается множество всех чисел х, которые удовлетворяют неравенствам a < x < b, если a и b два действительных числа и а < b, и обозначается (a, b). Открытый интервал не имеет ни наименьшего, ни наибольшего числа: какое бы число x Î (a, b) мы ни взяли, обязательно на этом интервале найдутся такие x¢ и x², что x¢ > x и x² < x. Множество всех точек любого интервала является бесконечным.

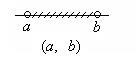
Замкнутый интервал (числовой отрезок) [a, b] состоит из всех чисел х, для которых a £ x £ b. Таким образом, [a, b] = (a, b) È {a} È {b}.

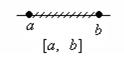
Интервалы смешанного типа: [a, b) = (a, b) È {a}; (a, b] = (a, b) È {b}. Числовые интервалы можно изобразить геометрически на числовой прямой следующим образом:

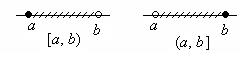
Заштрихованная часть числовой прямой содержит все точки, принадлежащие соответствующему интервалу. Незакрашенные кружочки означают, что эти точки не принадлежат интервалу, а закрашенные, наоборот, означают, что эти точки принадлежат интервалу.

Бесконечные интервалы.Интервал (–¥, a) (или (–¥, a]) – это множество всех чисел х, удовлетворяющих неравенству x < a (или x £ a). Интервал (а, +¥) (или [a, +¥)) – это множество таких чисел х, которые удовлетворяют неравенству x > a (или x ³ a). Интервал (–¥, +¥) – это множество R всех действительных чисел. Эти интервалы геометрически изображаются так:

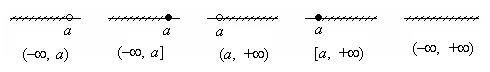
Фигурирующие в этих обозначениях символы +¥ и –¥ ни в коем случае нельзя понимать как действительные числа. Наличие символа +¥ в обозначении интервала означает, что интервал содержит любые сколь угодно большие числа (например, интервал (а, +¥) содержит все числа, большие а). По аналогии с обычным интервалом можно записать, что интервал (а, +¥) состоит из всех чисел х – таких, что a < x <+¥. Но фигурирующее в этой записи неравенство x < +¥ означает лишь, что х – любое действительное число, поэтому интервал (а, +¥) задается на самом деле одним неравенством x > a.

Точно так же наличие символа –¥ в обозначении интервала означает, что в этот интервал входят все отрицательные числа, абсолютные величины которых могут быть сколь угодно большими. Неравенство x > –¥, равно как и неравенство –¥ < x < +¥, означает, что х – произвольное действительное число.

Окрестность точки

Окрестностью точки x₀ называется любой открытый интервал, содержащий эту точку (рисунок 1). Открытый интервал (a, b) служит окрестностью всякой принадлежащей ему точки.

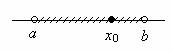
Рисунок 1

Возьмем какое-либо положительное число e. e-окрестностью точки x₀называется открытый интервал с центром в точке x₀ длиной 2e, то есть интервал (x₀ – e, x₀ + e). e-окрестность точки x₀ изображена на рисунке 2. Забегая вперед (см. п. 3), скажем, что можно задать e-окрестность точки x₀ и в виде неравенства |x – x₀| < e.

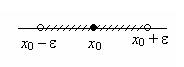
Рисунок 2

Пример.Пусть A, B, C – множества действительных чисел: A = (–4, 7); B = [0, 10], C = [–1, 4). Числовые промежутки A, B, C изображены на рисунке 3. Светлыми кружками обозначены концы промежутка, не принадлежащие ему (так, у интервала оба конца – светлые); закрашенными – принадлежащие промежутку.

Рисунок 3

Тогда

A ∩ B = [0, 7); A È B = (–4, 10]; A \ B = (–4, 0); B \ A = [7, 10]; C \ A = Æ; A \ C = (–4, –1) È [4, 7).

Упражнение. Покажите на числовой прямой множества B ∩ C, B È C, B \ C, C \ B, A ∩ C,
A È C , 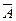, , 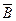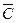и представьте эти промежутки с помощью введенных выше обозначений.

Замечание. Следует отметить, что одинаковым образом определяются и обозначаются числовые промежутки как в области действительных чисел (и тогда промежуток содержит бесконечное множество чисел), так и в области целых чисел (тогда, например, целочисленный отрезок [–3, 2] содержит 6 чисел: {–3, –2, –1, 0, 1, 2}, а интервал (–3, 2) содержит 4 числа:
{–2, –1, 0, 1}. Разница определяется тем, какое множество выбрано в качестве универсального

Множества точек, задаваемые алгебраическими уравнениями и неравенствами

С каждым уравнением связаны два числовых множества. Первое из них – область определения уравнения. Это множество состоит из всех значений х, для которых имеют смысл обе части уравнения. Второе множество – это множество его корней, то есть чисел, при подстановке которых в уравнение оно обращается в тождество.

Пример 1. Уравнение 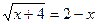имеет своей областью определения множество [–4, +¥). Найдем его корни. Возведем обе части уравнения в квадрат:

x + 4 = (2 – x)² или x² – 5x = 0.

Решим полученное квадратное уравнение:

x(x – 5) = 0 или x² – 5x = 0.

Оба числа x₁ = 0 и x₂ = 5 принадлежат множеству [–4, +¥), однако число x₂ = 5 является посторонним корнем уравнения (это показывает простая проверка: 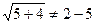). Таким образом, множество корней данного уравнения {0} Ì [–4, +¥). На прямой эти множества изображаются так:

Пример 2. Уравнение |x| = 3 имеет своей областью определения множество (–¥, +¥). Найдем его корни. По определению абсолютной величины числа х имеем

.

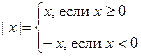Поэтому данное уравнение можно представить в виде совокупности двух уравнений: х = 3 и
–х = 3. Откуда получим два корня: x₁ = 3, x₂ = –3. Геометрически эти решения можно истолковать так: расстояние от x₁ до начала отсчета О и расстояние x₂ до начала отсчета О равны 3 (рисунок 4).

В случае уравнения |x – x₀| = a, где a > 0, имеем два корня: x₀ + a и x₀ – a. Геометрически расстояния от точки x₀ + a до x₀ и от точки x₀ – a до x₀ равны а (рисунок 5).

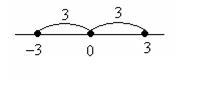
Рисунок 4

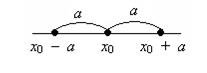
Рисунок 5

Пример 3. Неравенство |x| < 3 имеет своими решениями множество (–3, 3). Геометрически условие |x| < 3 приобретает следующий смысл: расстояние от точки х до начала отсчета меньше 3. Множество решений этого неравенства изображено на рисунке 6.

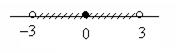
Рисунок 6

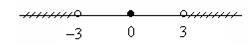
Рисунок 7

Пример 4.Неравенство |x| > 3 имеет своими решениями объединение двух множеств:
(–¥, –3) È (3, +¥). Геометрически условие |x| > 3 означает, что расстояние от точки х до начала отсчета больше 3. Множество решений этого неравенства изображено на рисунке 7.

В случае неравенства |x – x₀| < a, где a > 0, множество решений имеет вид (x₀ – a, x₀ + a) и является открытым интервалом длины 2а с центром в точке (рисунок 8).

Множество решений неравенства |x – x₀| > a, где a > 0, представляет собой объединение двух множеств (–¥, x₀ – a) È (x₀ + a, +¥). Эти множества изображены на рисунке 9.

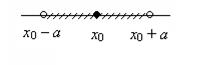
Рисунок 8

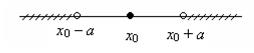
Рисунок 9

Объединив случаи уравнения |x – x₀| = a и неравенства |x – x₀| < a, получим множество реше-ний неравенства |x – x₀| £ a. Аналогично получается множество решений неравенства |x – x₀| ³ a.