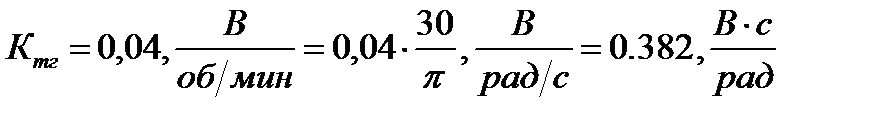Вывод необходимых уравнений. Определение численных значений постоянных времени и коэффициентов усиления при помощи данных таблиц

Показатели качества системы

Статическая ошибка	δст≤0.1º
Скоростная ошибка	δск≤0.2º
Время регулирования	τр≤0.15 с
Динамическая ошибка	Θ≤30 %

Следящая система - система, на выходе которой с определенной точностью воспроизводится произвольное во времени изменение какой-нибудь величины, поданной на вход. Следящие системы служат для изменения y(t) по заранее неизвестному закону.

Управляемым объектом данной системы является платформа с телескопом.

В данной следящей системе исполнительным элементом является двигатель постоянного тока с независимым возбуждением. В качестве измерительного устройства используется сельсинная пара (СД и СП являются одновременно чувствительными и преобразующими элементами) сельсинная пара также является элементом сравнения. Далее следует фазовый детектор и фильтр (ФД, Ф являются преобразующим элементом) для преобразования переменного тока сельсинной пары в постоянный ток усилителя. После усилителя ток поступает на якорь двигателя. Двигатель через редуктор передает вращение на вал платформы.

Так же в данной СУ имеется местная обратная связь, реализуемая с помощью тахогенератора (ТГ является чувствительным и преобразующим элементом). ТГ создает напряжение пропорциональное скорости вращения вала двигателя. Это напряжение подается непосредственно перед усилителем, где оно складывается с напряжением после фазового фильтра. Тем самым реализуется местная обратная отрицательная связь, по первой производной от угла. Главная обратная связь реализуется с помощью сельсин приемника.

Вывод необходимых уравнений. Определение численных значений постоянных времени и коэффициентов усиления при помощи данных таблиц.

Уравнение сельсинной пары: ΔU=K_cд(α_вх-α_вых) (1.1)

или ΔU=K_cдδ (1.2),

где δ= α_вх-α_вых (1.3) (рассоглосование)

Уравнение фазового детектора совместно с фильтром:

Для начала запишем передаточную функцию фазового детектора: 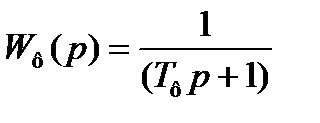(1.4)

Где,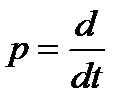

Уравнение движения ФД:

в передаточной форме:

U_ф=W_ф(p)·ΔU (1.5)

в дифференциальной форме

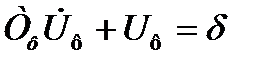(1.6)

Уравнение движения усилителя:

U_у=К_у(U_ф-U_тг) (1.7)

Где К_{у ­}– коэффициент усилителя, U_ф- напряжение с фазового детектора, U_тг – напряжение с тахогенератора.

Уравнение движения тахогенератора:

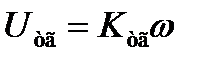(1.8)

где К_тг- коэффициент тахогенератора, 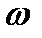- угловая скорость вращения двигателя

Уравнение движение двигателя:

По второму закону Кирхгофа:

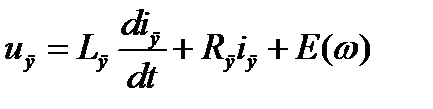, (1.9)

где u_я – напряжение управления, L_я и R_я – индуктивность и сопротивление цепи якоря, Е(ω) – противо ЭДС.

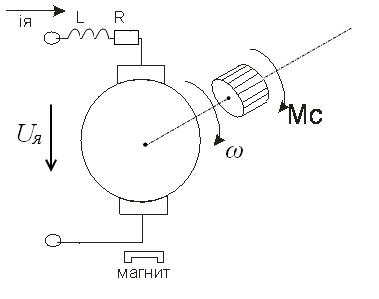
Рис.1.

По принципу Даламбера:

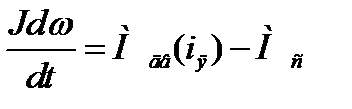, (1.10)

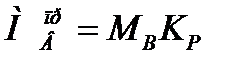(1.11)

где J– момент инерции, приведенный к валу двигателя, М_дв(i_я) – движущий момент, М_с – моментсопротивления приведенный к валу двигателя, М­_В- возмущающий момент на нагрузке, Кр- коэффициент редуктора.

Запишем эти два уравнения 1.9 и 1.10 в операторной форме:

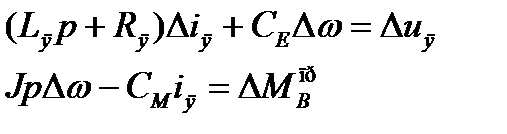
Исключив переменную 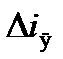, получим:

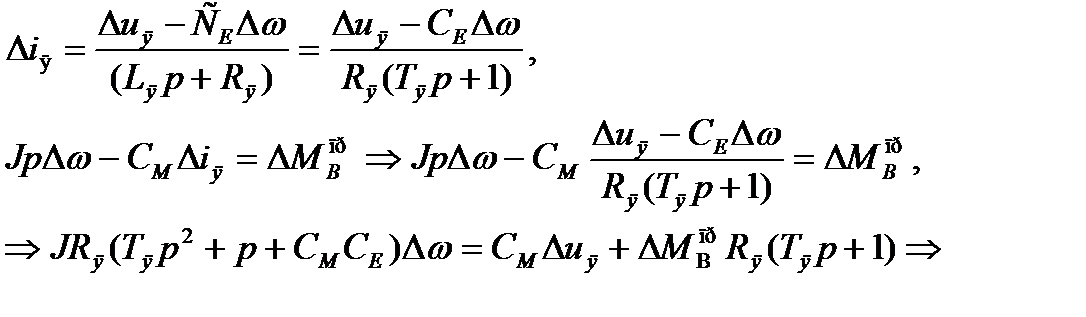
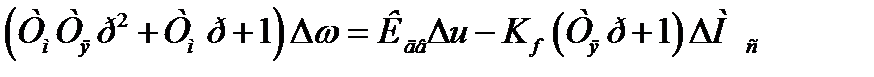
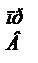(1.12)

где

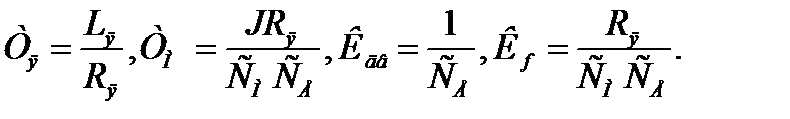
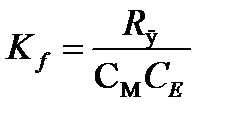
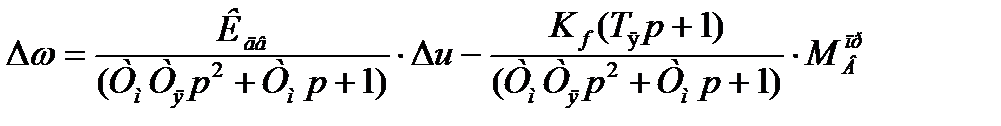(1.13)

Или

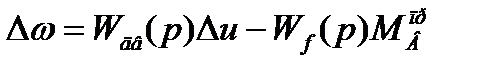(1.14)

Уравнение редуктора

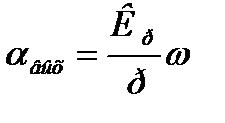(1.15)

где Кр - коэффициент редуктора.

Определение численных значений постоянных времени и коэффициентов усиления при помощи данных таблиц:

Проверка на работоспособность с заданным коэффициентом редуктора.

Найдем 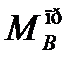по формуле (1.11)

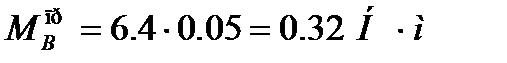
Чтоб двигатель имел возможность вращать платформу с телескопом необходимо выполнение следующего условия:

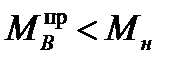
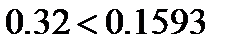
в данном случае это условие не выполняется, следовательно, придется изменить коэффициент редуктора. Примем K_P = 0.02, тогда:

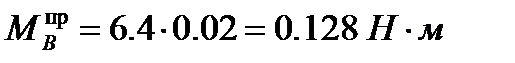
Теперь условие будет выполняться: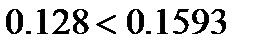

Эквивалентный момент инерции, приведенный к валу двигателя:

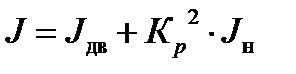
(1.16)

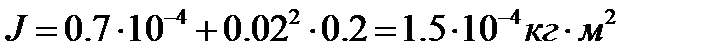
Номинальный вращающий момент:

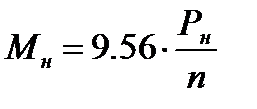(1.17)

где Р_н – номинальная мощность двигателя, n – номинальные обороты двигателя.

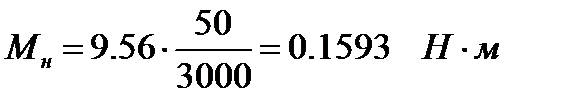
Коэффициент противоЭДС:

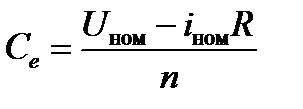(1.18)

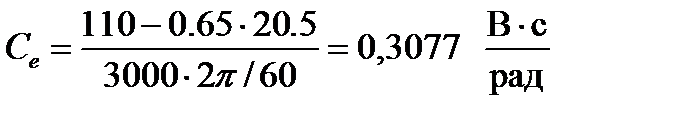
Коэффициент момента:

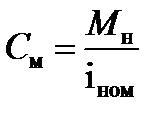(1.19)

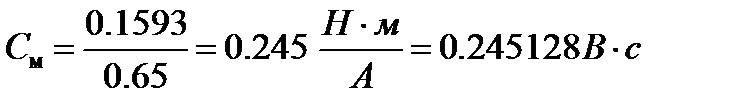
Постоянная времени якоря:

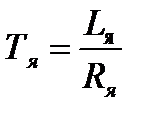
(1.20)
Т_я=0.115/20.5=0.0056098 с

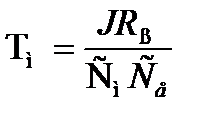
(1.21)
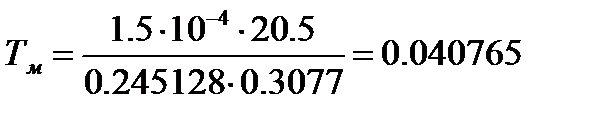с

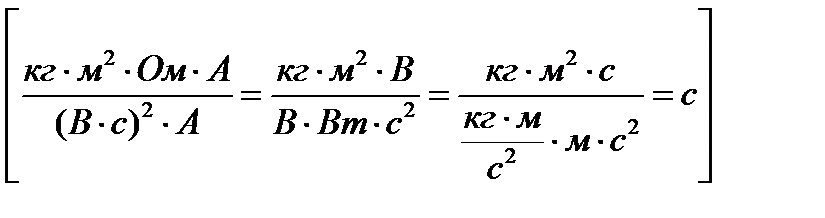
Коэффициент двигателя

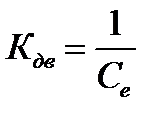
(1.22)

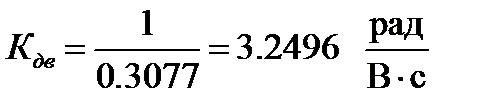
Коэффициент по возмущающему воздействию

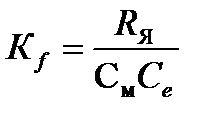
(1.23)

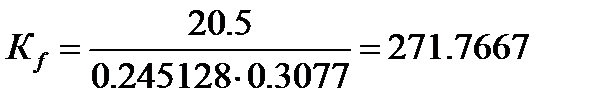
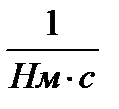
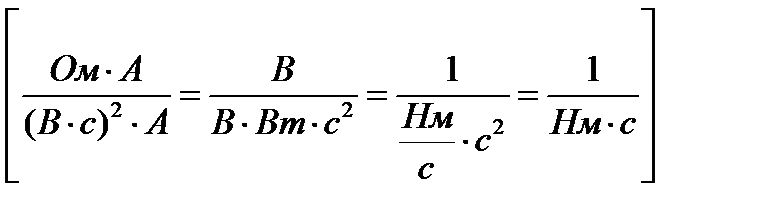
Коэффициент тахогенератора