| | | Определить, какие из следующих уравнений прямых являются нормальными: |
| | 309.1 |  ; ; |
| | 309.2 |  ; ; |
| | 309.3 |  ; ; |
| | 309.4 |  ; ; |
| | 309.5 |  ; ; |
| | 309.6 | 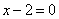 ; ; |
| | 309.7 | 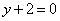 ; ; |
| | 309.8 |  . .  |
| | | Привести общее уравнение прямой к нормальному виду в каждом из следующих случаев: |
| | 310.1 |  ; ; |
| | 310.2 |  ; ; |
| | 310.3 |  ; ; |
| | 310.4 | 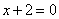 ; ; |
| | 310.5 |  . .  |
| | | Даны уравнения прямых. Определить полярный угол нормали 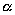 и отрезок p для каждой из данных прямых: по полученным значениям параметров и отрезок p для каждой из данных прямых: по полученным значениям параметров 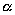 и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая 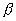 =300 и q=2). =300 и q=2). |
| | 311.1 | 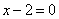 ; ; |
| | 311.2 | 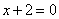 ; ; |
| | 311.3 | 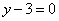 ; ; |
| | 311.4 | 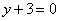 ; ; |
| | 311.5 |  ; ; |
| | 311.6 |  ; ; |
| | 311.7 |  ; ; |
| | 311.8 |  , q>0, , q>0, 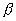 - острый угол. - острый угол. |
| | 311.9 |  , q>0, , q>0, 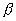 - острый угол. - острый угол.  |
| | | Вычислить величину отклонения 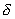 и расстояние d от точки до прямой в каждом из следующих случаев: и расстояние d от точки до прямой в каждом из следующих случаев: |
| | 312.1 | A(2; -1),  ; ; |
| | 312.2 | B(0; -3),  ; ; |
| | 312.3 | P(-2; 3),  ; ; |
| | 312.4 | Q(1; -2),  . .  |
| | | Установить, лежат ли точка М(1; -3) и начало координат по одну или разные стороны каждой из следующих прямых: |
| | 313.1 | 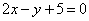 ; ; |
| | 313.2 |  ; ; |
| | 313.3 | 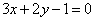 ; ; |
| | 313.4 | 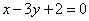 ; ; |
| | 313.5 |  . .  |
| | | Точка А(2; -5) является вершиной квадрата, одна из сторон которого лежит на прямой  . Вычислить площадь этого квадрата. . Вычислить площадь этого квадрата.  |
| | | Даны уравнения двух сторон прямоугольника  , ,  и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника. и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника.  |
| | | Доказать, что прямая  пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7). пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7).  |
| | | Доказать, что прямая  не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2). не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2).  |
| | | Последовательные вершины четырехугольника суть точки A(-1; 6), B(-1; -4), C(7; -1), D(2; 9). Установить, является ли этот четырехугольник выпуклым.  |
| | | Последовательные вершины четырехугольника суть точки A(-1; 6), B(1; -3), C(4; 10), D(9; 0). Установит, является ли этот четырехугольник выпуклым.  |
| | | Даны вершины треугольника A(-10; -13), B(-2; 3), C(2; 1). Вычислить длину перпендикуляра, оущенного из вершины В на медиану, проведенную из вершины С.  |
| | | Стороны АВ, ВС, СА треугольника АВС, соответственно даны уравнениями  , ,  , ,  . Вычислить расстояние от центра масс этого треугольника до стороны ВС. . Вычислить расстояние от центра масс этого треугольника до стороны ВС.  |
| | | Вычислить расстояние d между параллельными прямыми в каждом из следующих случаев: |
| | 322.1 |  , ,  ; ; |
| | 322.2 |  , ,  ; ; |
| | 322.3 |  , ,  ; ; |
| | 322.4 |  , ,  . .  |
| | | Две стороны квадрата лежат на прямых  , ,  . Вычислить его площадь. . Вычислить его площадь.  |
| | | Доказать, что прямая  параллельна прямым параллельна прямым  , ,  и делит расстояние между ними пополам. и делит расстояние между ними пополам.  |
| | | Даны параллельные прямые  , ,  , , 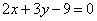 . Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними. . Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.  |
| | | Доказать, что через точку Р(2; 7) можно провести две прямые так, чтобы их расстояния от точки Q(1; 2) были равны 5. Составить уравнения этих прямых.  |
| | | Доказать, что через точку Р(2; 5) можно провести две прямые так, чтобы их расстояния от точки Q(5; 1) были равны 3. Составить уравнения этих прямых.  |
| | | Доказать, что через точку С(7; -2) можно провести только одну прямую так, чтобы расстояние ее от точки А(4; -6) было равно 5. Составить ее уравнение.  |
| | | Доказать, что через точку В(4; -5) невозможно провести прямую, чтобы расстояние от точки С(-2; 3) было равно 12.  |
| | | Вывести уравнение геометрического места точек, отклонение которых от прямых  равно –2. равно –2.  |
| | | Составить уравнение прямых, параллельных прямой  и отстоящие от нее на расстояние d=3. и отстоящие от нее на расстояние d=3.  |
| | | Даны две смежные вершины квадрата А(2; 0) и В(-1; 4). Составить уравнения его сторон.  |
| | | Точка А(5; -1) является вершиной квадрата, одна из сторон которого лежит на прямой  . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.  |
| | | Даны уравнения двух сторон квадрата  , ,  и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата. и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата.  |
| | | Даны уравнения двух сторон квадрата  , ,  . Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата. . Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата.  |
| | | Отклонения точки М от прямых  , ,  равны соответственно –3 и –5. Определить координаты точки М. равны соответственно –3 и –5. Определить координаты точки М.  |
| | | Составить уравнение прямой, проходящей через точку Р(-2; 3) на одинаковых расстояниях от точек А(5; -1) и В(3; 7). |
| | |  |
| | | Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: |
| | 338.1 |  , ,  ; ; |
| | 338.2 |  , ,  ; ; |
| | 338.3 |  , ,  ; ;  |
| | | Составить уравнения биссектрис углов, образованных двумя пересекающимися прямыми: |
| | 339.1 |  , ,  ; ; |
| | 339.2 | 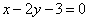 , ,  ; ; |
| | 339.3 | 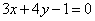 , ,  . .  |
| | | Составить уравнения прямых, которые проходят через точку Р(2; -1) и вместе с прямыми 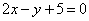 , ,  образуют равнобедренные треугольники. образуют равнобедренные треугольники.  |
| | | Определить, лежат ли точки М(1; -2) и начало координат в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых: |
| | 341.1 | 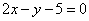 , ,  ; ; |
| | 341.2 |  , ,  ; ; |
| | 341.3 |  , ,  . .  |
| | | Определить, лежат ли точки М(2; 3) и N(5; -1) в одном, в смежных или вертикальных углах, образованных при пересечении двух прямых: |
| | 342.1 |  , ,  ; ; |
| | 342.2 |  , ,  ; ; |
| | 342.3 |  , ,  . .  |
| | | Определить, лежит ли начало координат внутри или вне треугольника, стороны которого даны уравнениями  , ,  , ,  . .  |
| | | Определить, лежит ли точка М(-3; 2) внутри или вне треугольника стороны которого даны уравнениями  , ,  , ,  . .  |
| | | Определить, какой из углов, острый или тупой, образованных двумя прямыми  , ,  содержит начало координат. содержит начало координат.  |
| | | Определить, какой из углов, острый или тупой, образованный двумя прямыми  , ,  , содержит точку М(2; -5). , содержит точку М(2; -5).  |
| | | Составить уравнение биссектрисы угла между прямыми  , ,  , в котором лежит начало координат. , в котором лежит начало координат.  |
| | | Составить уравнение биссектрисы угла между прямыми  , ,  , смежного с углом, содержащего начало координат. , смежного с углом, содержащего начало координат.  |
| | | Составить уравнение биссектрисы угла между прямыми  , ,  , в котором лежит точка М(1; -3). , в котором лежит точка М(1; -3).  |
| | | Составить уравнение биссектрисы угла между прямыми  , ,  , смежного с углом, содержащим точку С(2; -1). , смежного с углом, содержащим точку С(2; -1).  |
| | | Составить уравнение биссектрисы острого угла, образованного двумя прямыми  , ,  . .  |
| | | Составить уравнение биссектрисы тупого угла, образованного двумя прямыми  , ,  . .  |
 ;
;  ;
;  ;
;  ;
;  ;
; 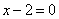 ;
; 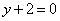 ;
;  .
. 
 ;
;  ;
;  ;
; 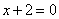 ;
;  .
. 
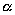 и отрезок p для каждой из данных прямых: по полученным значениям параметров
и отрезок p для каждой из данных прямых: по полученным значениям параметров 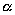 и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая
и р построить эти прямые на четеже (в последних двух случаях построение прямой выполнить, считая 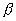 =300 и q=2).
=300 и q=2). 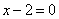 ;
; 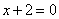 ;
; 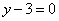 ;
; 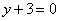 ;
;  ;
;  ;
;  ;
;  , q>0,
, q>0, 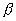 - острый угол.
- острый угол.  , q>0,
, q>0, 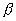 - острый угол.
- острый угол. 
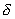 и расстояние d от точки до прямой в каждом из следующих случаев:
и расстояние d от точки до прямой в каждом из следующих случаев:  ;
;  ;
;  ;
;  .
. 
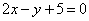 ;
;  ;
; 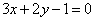 ;
; 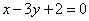 ;
;  .
. 
 . Вычислить площадь этого квадрата.
. Вычислить площадь этого квадрата. 
 ,
,  и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника.
и одна из его вершин А(-2; 1). Вычислить площадь этого прямоугольника. 
 пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7).
пересекает отрезок, ограниченный точками А(-5; 1), В(3; 7). 
 не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2).
не пересекает отрезка, ограниченного точками M1(-2; -3), M2(1; -2). 



 ,
,  ,
,  . Вычислить расстояние от центра масс этого треугольника до стороны ВС.
. Вычислить расстояние от центра масс этого треугольника до стороны ВС. 
 ,
,  ;
;  ,
,  ;
;  ,
,  ;
;  ,
,  .
. 
 ,
,  . Вычислить его площадь.
. Вычислить его площадь. 
 параллельна прямым
параллельна прямым  ,
,  и делит расстояние между ними пополам.
и делит расстояние между ними пополам. 
 ,
,  ,
, 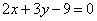 . Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними.
. Установить, что первая из них лежит между двумя другими, и вычислить отношение, в котором она делит расстояние между ними. 




 равно –2.
равно –2. 
 и отстоящие от нее на расстояние d=3.
и отстоящие от нее на расстояние d=3. 

 . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.
. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. 
 ,
,  и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата.
и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого квадрата. 
 ,
,  . Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата.
. Составить уравнения двух других его сторон при условии, что точка M1(-3; 5) лежит на стороне этого квадрата. 
 ,
,  равны соответственно –3 и –5. Определить координаты точки М.
равны соответственно –3 и –5. Определить координаты точки М. 

 ,
,  ;
;  ,
,  ;
;  ,
,  ;
; 
 ,
,  ;
; 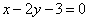 ,
,  ;
; 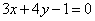 ,
,  .
. 
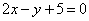 ,
,  образуют равнобедренные треугольники.
образуют равнобедренные треугольники. 
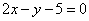 ,
,  ;
;  ,
,  ;
;  ,
,  .
. 
 ,
,  ;
;  ,
,  ;
;  ,
,  .
. 
 ,
,  ,
,  .
. 
 ,
,  ,
,  .
. 
 ,
,  содержит начало координат.
содержит начало координат. 
 ,
,  , содержит точку М(2; -5).
, содержит точку М(2; -5). 
 ,
,  , в котором лежит начало координат.
, в котором лежит начало координат. 
 ,
,  , смежного с углом, содержащего начало координат.
, смежного с углом, содержащего начало координат. 
 ,
,  , в котором лежит точка М(1; -3).
, в котором лежит точка М(1; -3). 
 ,
,  , смежного с углом, содержащим точку С(2; -1).
, смежного с углом, содержащим точку С(2; -1). 
 ,
,  .
. 
 ,
,  .
. 
