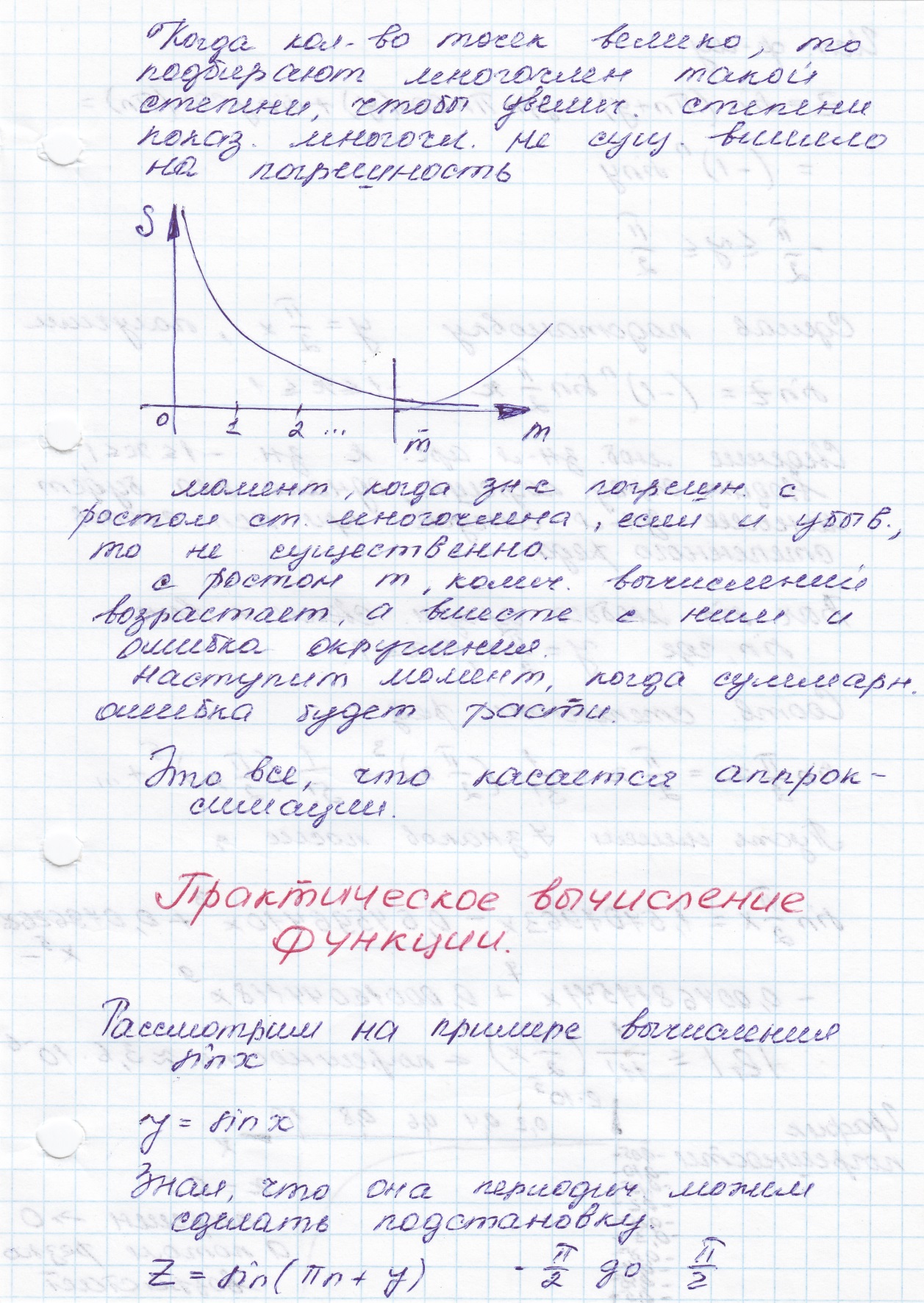
Подбор интерполяционного полинома методом наименьших квадратов

Погрешности. Источники погрешностей. Распространение погрешностей

(лекции)

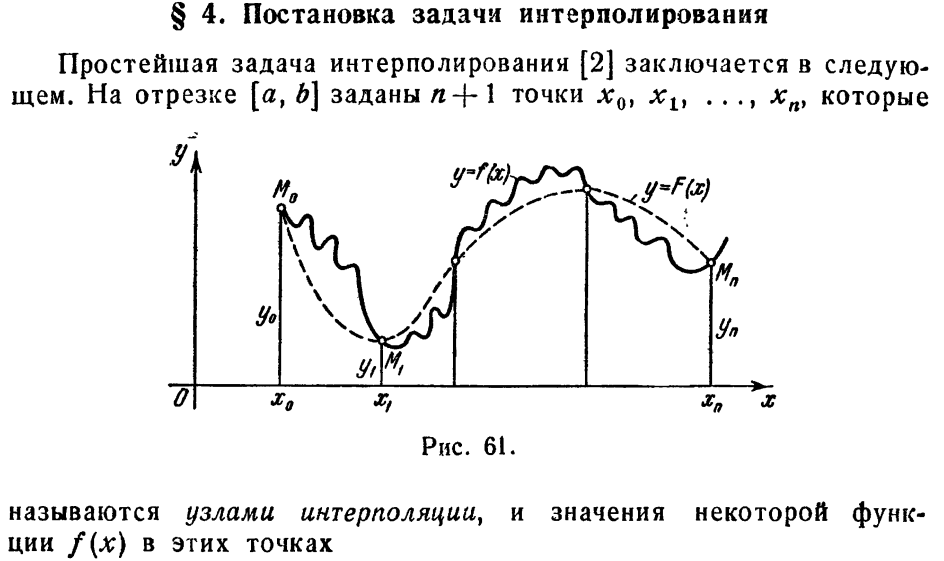
Интерполяция и экстраполяция. Конечные разности и их свойства.

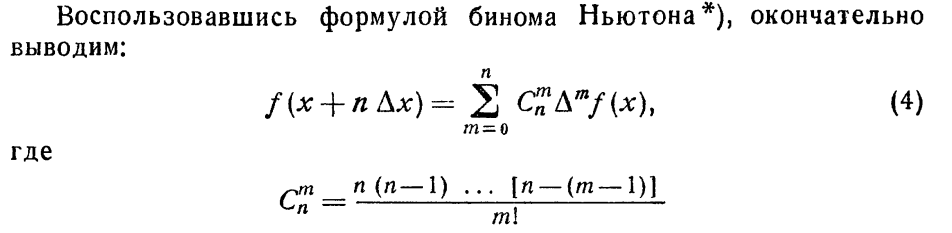
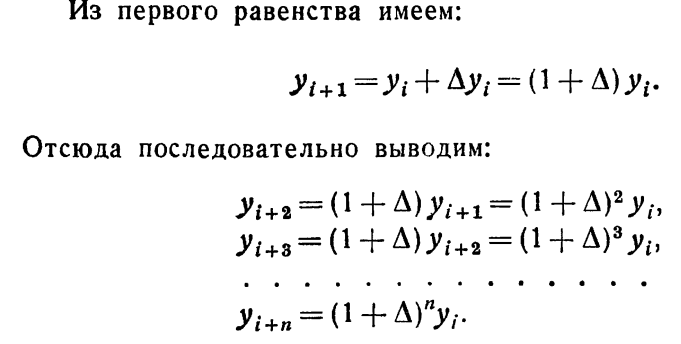
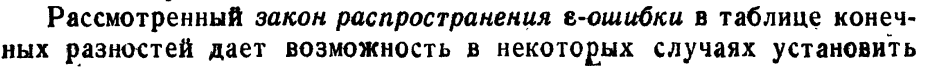
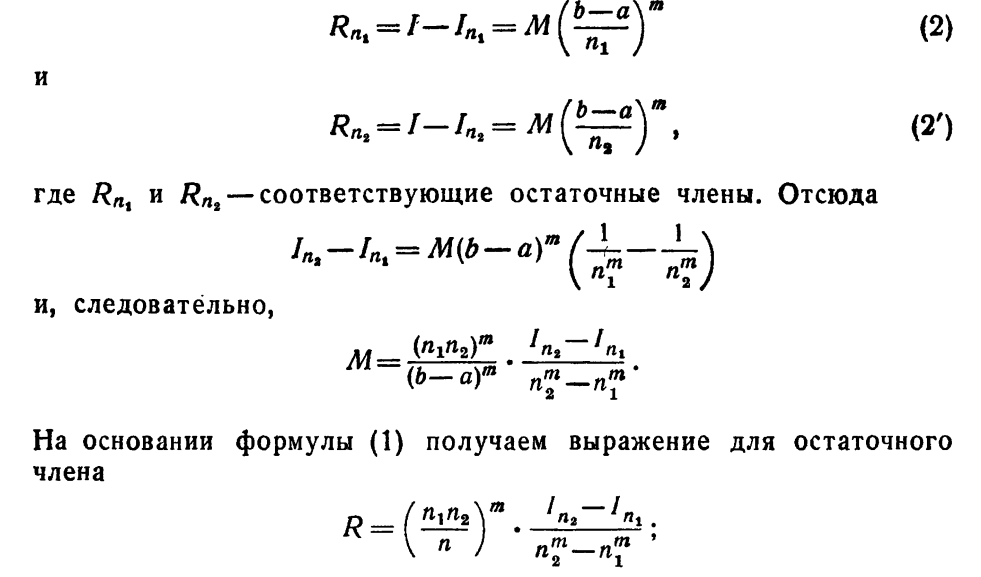
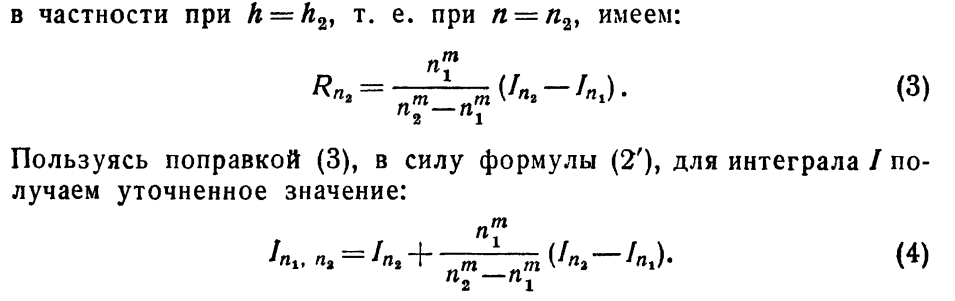
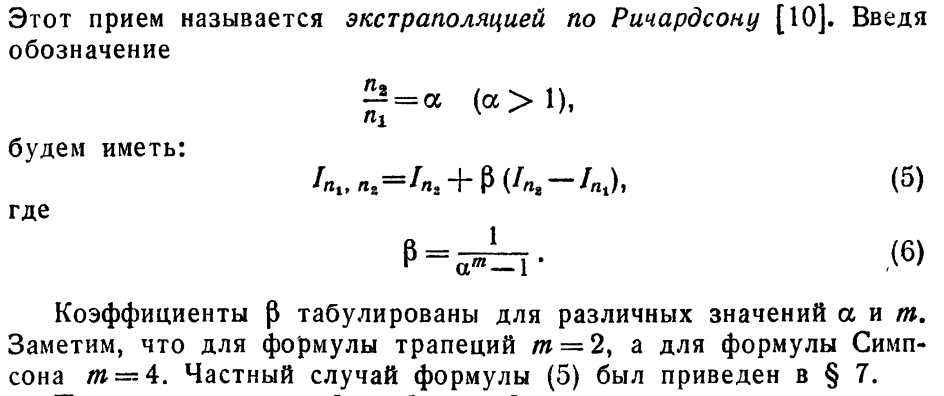
(лекции)

Обобщенная степень. Конечные разности от обобщенной снртепени.

(лекции)

Интерполяционные полиномы Ньютона.

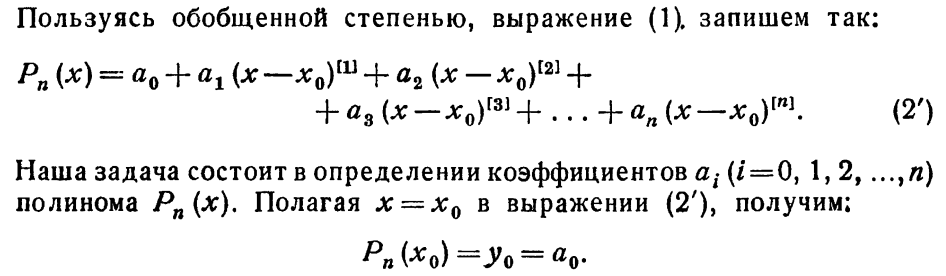
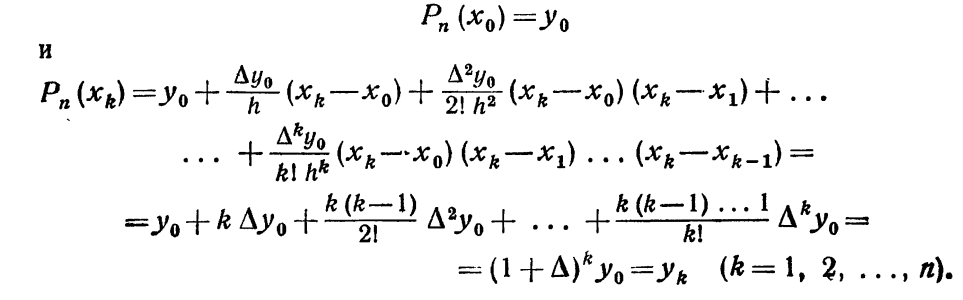
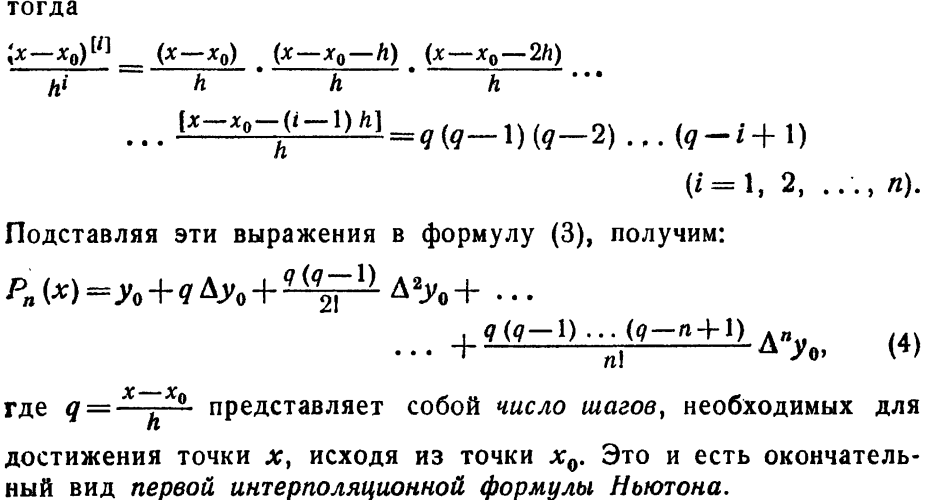
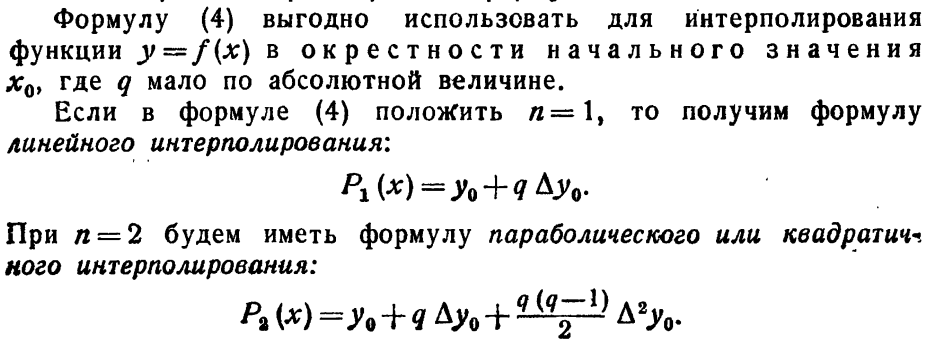
(лекции)

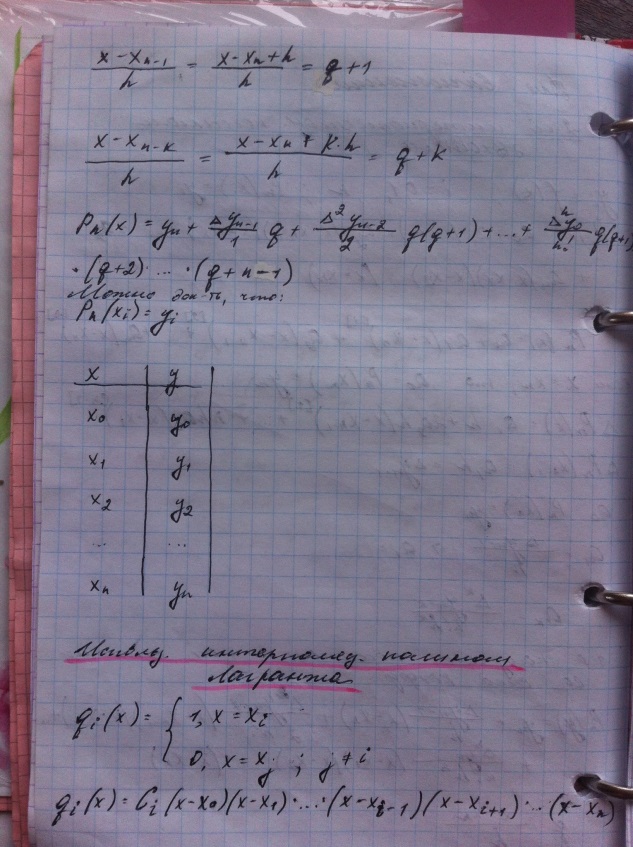
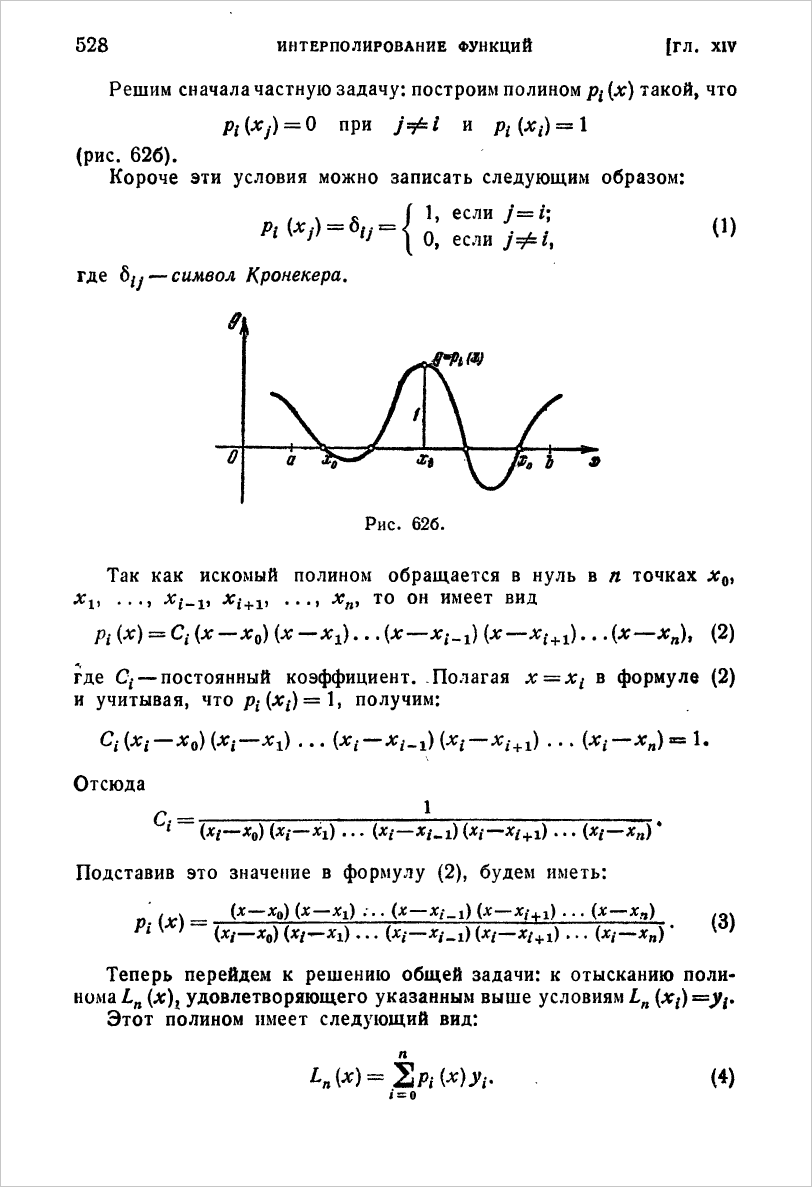
Интерполяционный полином Лагранжа. Алгоритм вычисления лагранжевых коэффициентов.

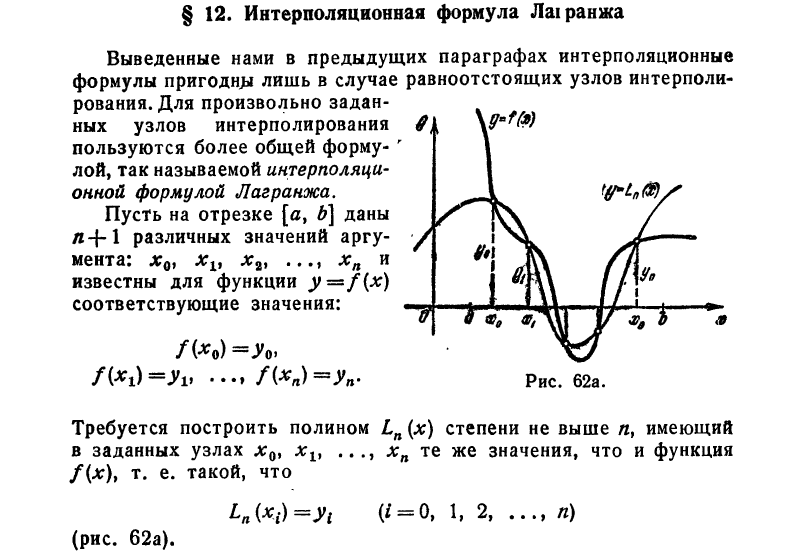
Подбор интерполяционного полинома методом наименьших квадратов

Сущность метода наименьших квадратов

Пусть 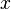— набор 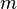неизвестных переменных (параметров), 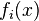, , 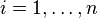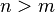— совокупность функций от этого набора переменных. Задача заключается в подборе таких значений x, чтобы значения этих функций были максимально близки к некоторым значениям 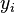. По существу речь идет о «решении» переопределенной системы уравнений 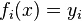, 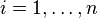в указанном смысле максимальной близости левой и правой частей системы. Сущность МНК заключается в выборе в качестве «меры близости» суммы квадратов отклонений левых и правых частей 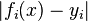. Таким образом, сущность МНК может быть выражена следующим образом:

.

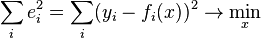В случае, если система уравнений имеет решение, то минимум суммы квадратов будет равен нулю и могут быть найдены точные решения системы уравнений аналитически или, например, различными численными методами оптимизации. Если система переопределена, то есть, говоря нестрого, количество независимых уравнений больше количества искомых переменных, то система не имеет точного решения и метод наименьших квадратов позволяет найти некоторый «оптимальный» вектор 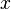в смысле максимальной близости векторов 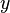и и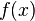ли максимальной близости вектора отклонений к нулю (близость понимается в смысле евклидова расстояния).

Пример — система линейных уравнений

В частности, метод наименьших квадратов может использоваться для «решения» системы линейных уравнений

,

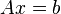где матрица 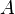не квадратная, а прямоугольная размера 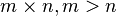(точнее ранг матрицы A больше количества искомых переменных).

Такая система уравнений, в общем случае не имеет решения. Поэтому эту систему можно «решить» только в смысле выбора такого вектора 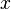, чтобы минимизировать «расстояние» между векторам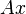и и 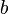. Для этого можно применить критерий минимизации суммы квадратов разностей левой и правой частей уравнений системы, то есть 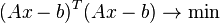. Нетрудно показать, что решение этой задачи минимизации приводит к решению следующей системы уравнений

.

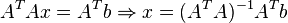Используя оператор псевдоинверсии, решение можно переписать так:

,

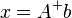где 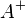— псевдообратная матрица для .

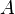Данную задачу также можно «решить» используя так называемый взвешенный МНК (см. ниже), когда разные уравнения системы получают разный вес из теоретических соображений.

Строгое обоснование и установление границ содержательной применимости метода даны А. А. Марковым и А. Н. Колмогоровым.