Теорема 1.Если две поверхности второго порядка пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.

Рассмотрим пример, к которому приложима теорема.

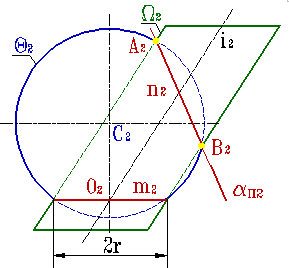
Фронтальные проекции q₂ сферы Q и W₂ эллиптического цилиндра W, имеющих общую окружность m(m₂) с центром О(О₂) (рис.8.36).

		а) модель	б) эпюр
Рисунок 8.36. Пересечение сферы и эллиптического цилиндра

Плоскость σ, определяемая центром сферы С и осью i цилиндра, является плоскостью симметрии заданных поверхностей, и параллельна фронтальной плоскости проекций.

Общая окружность радиуса r – это одна из плоских кривых второго порядка распавшейся линии пересечения. Остается построить вторую кривую, плоскость α которой должна быть в условиях данного примера перпендикулярна плоскости симметрии σ, а следовательно и П₂. Вторая линия пересечения (окружность) проецируется на П₂ в виде отрезка прямой n₂. Для ее построения следует воспользоваться точками А₂ и В₂, принадлежащими очеркам заданных поверхностей.

Теорема 2.(о двойном касании). Если две поверхности второго порядка имеют касание в двух точках А и В, то линия их пересечения распадается на две плоские кривые второго порядка, плоскость которых проходит через отрезок АВ, соединяющий точки касания.

		а) модель	б) эпюр
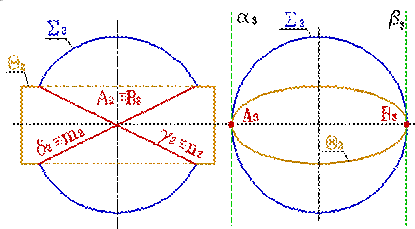
Рисунок 8.37 Пересечение сферы и эллиптического цилиндра имеющих две точки касания

Например, по двум окружностям m и n пересекается сфера S и эллиптический цилиндр Q (рис.8.37). Точки касания и касательные плоскости обозначены соответственно через А, В, α, β. Окружности, на которые распалась линия пересечения поверхностей, расположены во фронтально- проецирующих плоскостях γ и δ.

Теорема 3. (теорема Г. Монжа). Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания.

		а) модель	б) эпюр
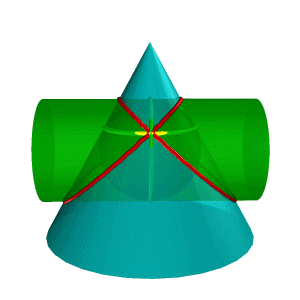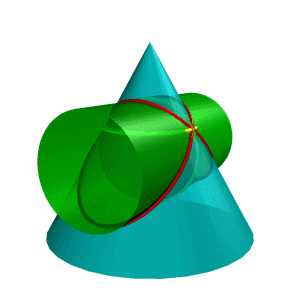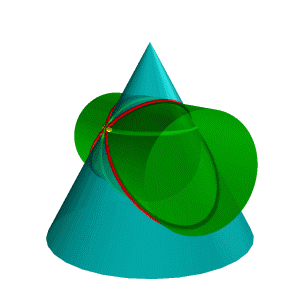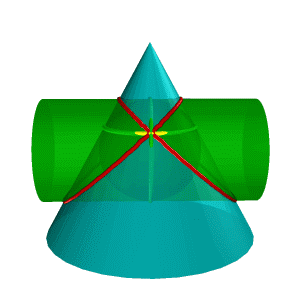
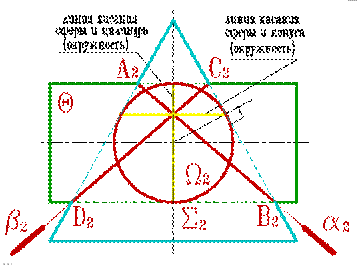
Рисунок 8.38. Пересечение конуса и цилиндра имеющих общую вписанную сферу

В соответствии с этой теоремой линия пересечения конуса Σ и цилиндра Q (рис.8.38), описанных около сферы W, будут плоскими кривыми – эллипсами (расположенными в плоскостяхa и b), фронтальные проекции которых изображаются прямыми А₂В₂ и С₂Д₂,

Теорема Монжа находит эффективное применение при конструировании трубопроводов.

Теорема 4. Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту плоскость в виде кривой второго порядка.

а) модель	б) эпюр
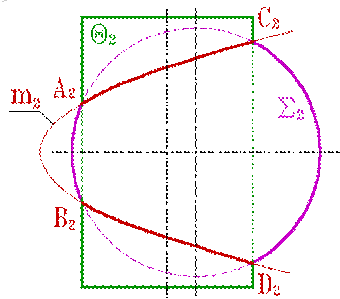
Рисунок 8.39. Пересечение сферы и цилиндра

Плоскость симметрии определена осью симметрии цилиндра Q и центром сферы S (рис.8.39). Плоскости принадлежат и симметричные сами себе точки A, B, CиD линий пересечения. Проекция же линий на фронтальную плоскость имеет форму параболы m₂ и аналитически описывается формулой параболы.

Лекция №8 часть 4

Развертка поверхности. Основные свойства развертки. Развертка поверхности многогранников. Развертка цилиндрической поверхности. Развертка конической поверхности. Задание касательной плоскости на эпюре Монжа. Поверхность касательная к поверхности.

Развертка поверхности

Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.

Основные свойства развертки

1. Длины двух соответствующих линий поверхности и ее развертки равны между собой;

2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

3. Прямой на поверхности соответствует также прямая на развертке;

4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

5. Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.