Доказать, что если биссектрисы треугольника разбивают его на шесть равных по площади треугольников, то данный треугольник – правильный. (http://www.Tutoronline.Ru)
МЕТОД ДОКАЗАТЕЛЬСТВА ОТ ПРОТИВНОГО
Суть этого метода заключается в следующем:
1. Вначале делается предположение, противоположное тому, что требуется доказать.
2. Затем выясняется, что следует из сделанного предположения на основании уже преобретенных теоретических знаний (теорем, аксиом и т.д.) .
3. Устанавливается несоответствие (противоречие) предположения с теоретическими данными (теорем, аксиом и т.д.) или условием задач.
4. Делается вывод о том, что наше предположение не верно, а верно утверждение ему противоположное т.е. то, что требуется доказать.
Ключевые задачи:
Задача 1.
Доказать, что если биссектрисы треугольника разбивают его на шесть равных по площади треугольников, то данный треугольник – правильный.
Задача 2.
Какое наибольшее число острых углов может быть в выпуклом многоугольнике?
Задача 3.
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
Элементарные задачи:
Задача 4.
Прямые а и b такие, что любая прямая, которая пересекает а, пересекает и b.Доказать, что а ll b.
Задача 5.
Прямые а и b – параллельные, прямые а и с пересекаются. Докажите, что прямые b и с пересекаются.
Задачи для самостоятельной работы:
Задача 6.
A, В, С — точки прямой а, АВ = 5 см, АС = 2 см, ВС = 7 см. Докажите, что точка С не лежит между точками А и В.
Задача 7.
Прямая а перпендикулярна отрезку АВ и пересекает данный отрезок в его середине. Докажите, что каждая точка, равноудаленная от точек A и B лежит на прямой а.
Задача 8.
На сторонах AB и BC треугольника ABC выбраны точки M и N соответственно. Отрезки AN и CM пересекаются в точке O , причём AO=CO . Обязательно ли треугольник ABC равнобедренный, если AM=CN.
Задача 9.
Доказать, что выпуклый четырехугольник с разными углами должен иметь хотя бы один тупой угол.
Задача 10.
Докажите, что не существует треугольной пирамиды, у которой к каждому ребру примыкает тупой угол на одной из граней.
ДОКАЗАТЕЛЬСТВО ЗАДАЧ
Задача 1.
Доказать, что если биссектрисы треугольника разбивают его на шесть равных по площади треугольников, то данный треугольник – правильный. (http://www.tutoronline.ru)
Доказательство.
1) Очевидно, что треугольник правильный, если его биссектрисы одновременно являются и его медианами.
2) Биссектриса, проходящая через точку пересечения медиан, является и медианой треугольника.
Вывод: надо доказать, что если три прямых, проходящих через вершины треугольника, пересекаются в одной его внутренней точке М и разбивают треугольник на шесть равных по площади, то М – точка пересечения медиан.
Рассмотрим треугольник ABC (рис. 1), где АА1, ВВ1, СС1 – медианы, а М0 – точка их пересечения.
. 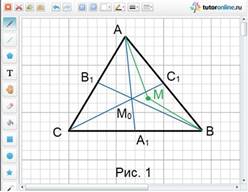
Шесть полученных треугольников с вершиной М0 имеют одинаковую площадь, поэтому треугольники АВМ0, ВСМ0 и АСМ0 так же имеют одинаковую площадь.
Теперь используем метод «от противного».
Пусть точка М не совпадает с точкой М0. Рассмотрим треугольники АВМ, АСМ и ВСМ. Из условия вытекает, что площади этих треугольников равны (площадь каждого равна 1/3 площади DАВС). Точка М должна попасть внутрь или на сторону одного из треугольников АВМ0, АСМ0 или ВСМ0 (предположим, что внутрь треугольника АВМ0).
Очевидно, что SDАВМ < SDАВМ0 = 1/3 · SDАВС.
Итак, получено противоречие, т.к. с одной стороны, SDАВМ = 1/3 · SDАВС, а с другой – она меньше.
Из этого следует, что предположение о том, что М не совпадает с М0 ошибочно, поэтому имеем, что М0 = М.
Таким образом, доказано, что биссектрисы проходят через точку пересечения медиан, то есть биссектрисы являются медианами, а это верно только для правильных треугольников.
Задача 2.
Какое наибольшее число острых углов может быть в выпуклом многоугольнике?
(www.ref.by.)
Решение.
Легко показать, что три острых угла в многоугольнике может быть (например, в треугольнике). Все попытки построить какой-нибудь выпуклый n-угольник с четырьмя острыми углами оказываются тщетными. Возникает гипотеза: максимальное количество острых углов выпуклого многоугольника – три. Докажем ее.
1) Пусть найдется выпуклый многоугольник с большим числом углов,
например, с четырьмя.
2) В этом случае сумма четырех острых углов будет меньше, чем 90°•4 или 180°•2. Сумма же остальных n – 4 углов будет меньше, чем 180°•(n – 4). Тогда сумма всех углов n-угольника меньше, чем 180°•2 + 180°•(n – 4) = 180°•(n – 2), а это невозможно для выпуклого n-угольника (сумма его углов равна 180°•(n – 2)).
3) Полученное противоречие кроется в исходном предположении.
4) Наше предположение относительно существования четырех (а как показывает анализ рассуждений и большего количества) острых углов неверно. Следовательно, максимальное количество острых углов выпуклого n- угольника – три.
Доказательство выдвинутой гипотезы завершает решение задачи.
Задача 3.
Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны. (www.webmath.exponenta.ru)
Доказательство.
Пусть (AB) || (CD). Предположим, что 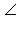 ACD ≠ ACD ≠ 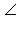 BAC. Через точку A проведем прямую AE так, что BAC. Через точку A проведем прямую AE так, что 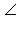 EAC = EAC = 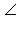 ACD. Но тогда по теореме «Если внутренние накрест лежащие углы равны, то прямые параллельны.» (AE) || (CD), а по условию – (AB) || (CD). В соответствии с теоремой «Две прямые, параллельные третьей, параллельны.» (AE) || (AB). Это противоречит теореме, по которой через точку A, не лежащую на прямой CD, можно провести единственную прямую, параллельную ей. Теорема доказана. ACD. Но тогда по теореме «Если внутренние накрест лежащие углы равны, то прямые параллельны.» (AE) || (CD), а по условию – (AB) || (CD). В соответствии с теоремой «Две прямые, параллельные третьей, параллельны.» (AE) || (AB). Это противоречит теореме, по которой через точку A, не лежащую на прямой CD, можно провести единственную прямую, параллельную ей. Теорема доказана.
|
Задача 4.
Прямые а и b такие, что любая прямая, которая пересекает а, пересекает и b.Доказать, что а ll b. (Доказательство от противного. Лещенко В. Ю.)
Доказательство.
Возможны только два случая:
1) прямые а и b параллельны;
2) прямые а и b не параллельны.
Если удастся исключить нежелательный случай, то останется сделать вывод, что имеет место второй из двух возможных. Чтобы отбросить нежелательный случай, давайте подумаем, что произойдёт, если прямые а и b пересекаются:
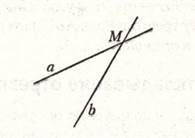
По условию любая прямая, которая пересекает а, пересекает и b. Поэтому, если удастся найти хотя бы одну прямую, которая пересекает а, но не пересекает b, этот случай надо будет отбросить. Таких прямых можно найти сколько угодно: достаточно провести через любую точку К прямой а, кроме точки М прямую КС, параллельную b:
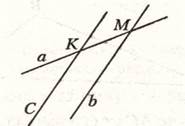
Поскольку отброшен один из двух возможных случаев, можно сразу сделать вывод, что а ll b.
Задача 5.
Прямые а и b – параллельные, прямые а и с пересекаются. Докажите, что прямые b и с пересекаются.
Доказательство.
1) Предположим, что b||с.
2) Тогда получается, что через точку О (точка пересечения прямых а и с) проходят две различные прямые а и b, которые параллельны прямой b.
3) Это противоречит аксиоме параллельных прямых.
Вывод: значит, наше предположение неверно, а верно то, что и требовалось доказать, т. е. что прямые b и с пересекаются.
Задача 6.
A, В, С — точки прямой а, АВ = 5 см, АС = 2 см, ВС = 7 см. Докажите, что точка С не лежит между точками А и В. (Доказательство от противного. Ващенко В. Н.)
Доказательство.
1) Предположим, что точка С лежит между точками А и В.
2) Тогда по аксиоме измерения отрезков АВ = АС + СВА
3) Это противоречит условию: АВ = АС + СВ, так как АВ = 5 см, АС+ С5 = 9 см.
Вывод: точка С не лежит между точками А и В.
Задача7.
Прямая а перпендикулярна отрезку АВ и пересекает данный отрезок в его середине. Докажите, что каждая точка, равноудаленная от точек A и B лежит на прямой а. (Геометрическое место точек. Ипатова Я. Г. )
Доказательство.
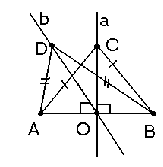
Предполагаем, что существует такая точка D, что AD=DB, построим прямую DO и соединим D и O.
Рассмотрим ∆ADB, он равнобедренный по определению, т.к. AD=DB. DO-медиана равнобедренного треугольника, тогда DO- высота (по теореме о медиане равнобедренного треугольника), тогда DO ┴ AB, a┴ AB, через точку О можно провести только одну прямую перпендикулярную отрезку AB. Значит наше предположение о том, что точка D принадлежит другой прямой, а не прямой a - ложно.
Задача 8.
На сторонах AB и BC треугольника ABC выбраны точки M и N соответственно. Отрезки AN и CM пересекаются в точке O , причём AO=CO . Обязательно ли треугольник ABC равнобедренный, если AM=CN.( http://collection.edu.yar.ru)
Доказательство.
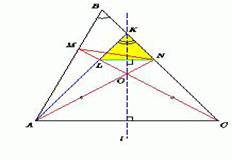
Рассмотрим треугольник ABC , в котором
 ABC=60o,
ABC=60o,  BAC = 45o,
BAC = 45o,  ACB = 75o.
ACB = 75o.
Отметим на серединном перпендикуляре к стороне AC точку O , для которой  OAC =
OAC =  OCA = 30o (рис.). Пусть луч AO пересекает сторону BC в точке N , а луч CO пересекает сторону AB в точке M . Тогда
OCA = 30o (рис.). Пусть луч AO пересекает сторону BC в точке N , а луч CO пересекает сторону AB в точке M . Тогда
 ANC = 75o,
ANC = 75o,  OMA = 105o.
OMA = 105o.
При симметрии относительно серединного перпендикуляра к стороне AC точка M переходит в точку M" , лежащую на отрезке ON . При этом
 OM"C =
OM"C =  OMA = 105o,
OMA = 105o,  CM"N = 180o -
CM"N = 180o -  OM"C = 180o - 105o = 75o =
OM"C = 180o - 105o = 75o =  CNM".
CNM".
Значит, треугольник CNM" – равнобедренный. Следовательно,
CN = CM"=AM.
Таким образом, неравнобедренный треугольник ABC удовлетворяет условию AM=CN.
Задача 9.
Доказать, что выпуклый четырехугольник с разными углами должен иметь хотя бы один тупой угол. (Геометрические задачи на доказательство. Дубина С. В.)
Решение:
Допустим, что выпуклый четырехугольник с неравными углами не имеет тупых углов, тогда все внешние углы его тупые и сумма их больше 3600, что противоречит теореме о сумме углов выпуклого многоугольника. Значит, предположение неверно, и четырехугольник имеет хотя бы один тупой угол.
Задача 10.
Докажите, что не существует треугольной пирамиды, у которой к каждому ребру примыкает тупой угол на одной из граней.(Идеи и методы решения задач. Софут В. А.)
Решение.
Допустим, что такая пирамида существует. Поскольку в треугольнике против тупого угла лежит самая длинная сторона, то для каждого ребра найдётся более длинное ребро. Это невозможно, так как количество рёбер у пирамиды конечно. Противоречие.
Замечание. Вместе с рассуждением от противного мы использовали «Правило крайнего».