Проверка коэффициента перекрытия
Если условие отсутствия подрезания (5.66) выполняется для обоих колес пары, то коэффициент перекрытия находят по известной формуле
 ; (5.70)
; (5.70)
если условие (5.66) не выполняется, то для каждого колеса, зубья которого подрезаны, следует произвести проверку неравенства
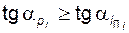 . (5.71)
. (5.71)
При соблюдении (5.71) величину подрезания для соответствующего колеса условимся считать допустимой, поскольку оно не укорачивает активный профиль подрезанного зуба и, следовательно, не влияет на величину коэффициента перекрытия (которую в этом случае находят по той же формуле (5.70)).
Если неравенство (5.71) не выполняется хотя бы для одного из колес пары, величину e следует считать по формуле
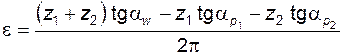 ; (5.72)
; (5.72)
в (5.72) подставляют 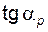 для того колеса, которое не подрезано или для которого условие (5.71) выполняется и
для того колеса, которое не подрезано или для которого условие (5.71) выполняется и 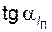 (вместо
(вместо 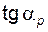 ) – для которого оно не выполняется. В этом случае вопрос о допустимости подрезания должен решаться индивидуально: в зависимости от степени ответственности проектируемой передачи и получившегося при расчете значения коэффициента перекрытия.
) – для которого оно не выполняется. В этом случае вопрос о допустимости подрезания должен решаться индивидуально: в зависимости от степени ответственности проектируемой передачи и получившегося при расчете значения коэффициента перекрытия.
5.9. Выбор коэффициентов смещения с помощью
блокирующих контуров
Блокирующий контур (БК) – это совокупность линий в системе координат  и
и  , ограничивающих зону допустимых коэффициентов смещения для передачи с числами зубьев
, ограничивающих зону допустимых коэффициентов смещения для передачи с числами зубьев 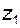 и
и 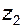 .
.
В изданных альбомах блокирующих контуров принято, что 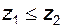 .
.
Форма БК и перечень линий, входящих в его состав, напрямую зависят от чисел зубьев колес 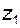 и
и 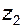 , системы расчета диаметров вершин колес, а также от геометрии применяемого зуборезного инструмента. Зону недопустимых коэффициентов смещения на контурах обычно отмечают штриховкой.
, системы расчета диаметров вершин колес, а также от геометрии применяемого зуборезного инструмента. Зону недопустимых коэффициентов смещения на контурах обычно отмечают штриховкой.
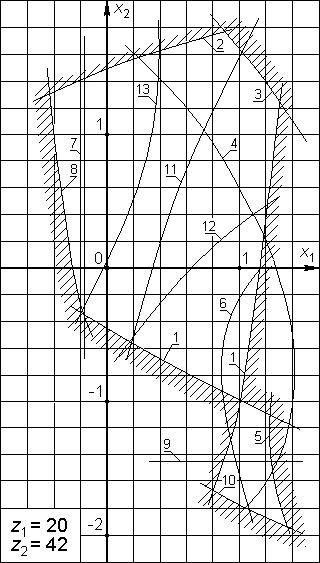 |
| Рис. 5.17 |
На рис. 5.17 в качестве примера приведен БК для пары  и
и 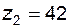 , колеса которой нарезаны стандартным инструментом реечного типа; расчет диаметров окружностей вершин обеспечивает в зацеплении стандартный радиальный зазор, равный
, колеса которой нарезаны стандартным инструментом реечного типа; расчет диаметров окружностей вершин обеспечивает в зацеплении стандартный радиальный зазор, равный 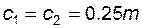 . Опишем линии, входящие в состав этого контура:
. Опишем линии, входящие в состав этого контура:
1 – линия ограничений по отсутствию интерференции у основания зуба колеса 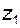 (состоит из двух ветвей, пересекающихся в точке с координатами (1; -1)); во всех точках этой линии
(состоит из двух ветвей, пересекающихся в точке с координатами (1; -1)); во всех точках этой линии 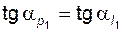 ;
;
2 – линия ограничений по отсутствию интерференции у основания зуба колеса 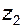 ; во всех точках этой линии
; во всех точках этой линии 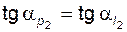 ;
;
3 – линия ограничений по коэффициенту перекрытия передачи 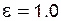 ;
;
4 – изолиния коэффициента перекрытия 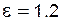 ;
;
5 – линия 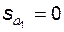 , ограничивающая БК по условию отсутствия заострения зуба колеса
, ограничивающая БК по условию отсутствия заострения зуба колеса 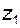 ;
;
6 – изолиния толщины зуба 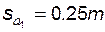 по дуге окружности вершин колеса
по дуге окружности вершин колеса 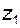 ;
;
7 – линия ограничений по подрезанию зубьев колеса 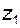 (вертикальная прямая); для всех точек этой линии
(вертикальная прямая); для всех точек этой линии 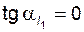 , или
, или 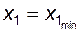 ;
;
8 – линия, ограничивающая зону, в которой подрезание зуба колеса 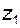 не укорачивает его активного профиля (для всех точек этой линии
не укорачивает его активного профиля (для всех точек этой линии 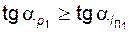 );
);
9 – линия ограничений по подрезанию зубьев колеса 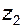 (горизонтальная прямая); для всех точек этой линии
(горизонтальная прямая); для всех точек этой линии 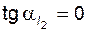 , или
, или 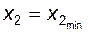 ;
;
10 – линия, ограничивающая зону, в которой подрезание зуба колеса 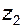 не укорачивает его активного профиля (для всех точек этой линии
не укорачивает его активного профиля (для всех точек этой линии 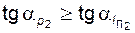 );
);
11 – линия выровненных удельных скольжений 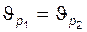 ; для справки – величина
; для справки – величина 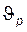 для каждого колеса, участвующего в зацеплении, характеризует отношение скорости скольжения к скорости перемещения контактной точки по профилю (вычисляются для нижних точек активных профилей зубьев); величины
для каждого колеса, участвующего в зацеплении, характеризует отношение скорости скольжения к скорости перемещения контактной точки по профилю (вычисляются для нижних точек активных профилей зубьев); величины 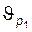 и
и 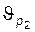 можно вычислить по формулам
можно вычислить по формулам
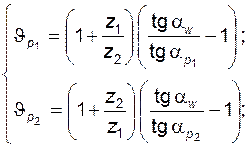 (5.73)
(5.73)
по одной из существующих гипотез, чем меньше по модулю каждая из величин 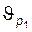 и
и 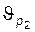 , и чем меньше они отличаются друг от друга, тем выше износостойкость передачи;
, и чем меньше они отличаются друг от друга, тем выше износостойкость передачи;
12 – линия изгибной равнопрочности зубьев при ведущем ко-
лесе 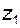 ;
;
13 – линия изгибной равнопрочности зубьев при ведущем ко-
лесе 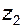 .
.
Линии БК, подобные кривым 1, 2, 3 и 5, являются безусловными границами области существования передачи.
При проектировании передачи выбор любого сочетания коэффициентов смещения  и
и  равносилен выбору некоторой точки
равносилен выбору некоторой точки 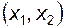 в системе координат БК; если эта точка окажется за пределами безусловных границ контура, то передача, составленная из колес, нарезанных с этими коэффициентами смещения, должна быть безоговорочно признана неработоспособной.
в системе координат БК; если эта точка окажется за пределами безусловных границ контура, то передача, составленная из колес, нарезанных с этими коэффициентами смещения, должна быть безоговорочно признана неработоспособной.
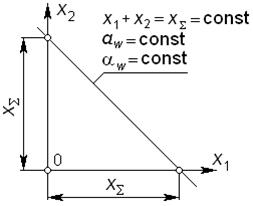
Отметим, что все сочетания коэффициентов  и
и  , при которых межосевое расстояние передачи
, при которых межосевое расстояние передачи  постоянно (при этом, очевидно, будут постоянными угол зацепления
постоянно (при этом, очевидно, будут постоянными угол зацепления  и коэффициент суммы смещений
и коэффициент суммы смещений  ), образуют геометрическое место – прямую, отсекающую на осях координат БК отрезки, равные
), образуют геометрическое место – прямую, отсекающую на осях координат БК отрезки, равные  (рис. 5.18).
(рис. 5.18).
 |
| Рис. 5.18 |
Свойства зубчатой пары, соответствующие выбранным значениям  и
и  , существенно зависят от расположения точки
, существенно зависят от расположения точки  относительно границ БК и этим широко пользуются при проектировании передачи.
относительно границ БК и этим широко пользуются при проектировании передачи.
В качестве примера рассмотрим несколько вариантов выбора коэффициентов смещения с помощью того же БК для пары  (рис. 5.19) при условии, что коэффициент перекрытия передачи должен удовлетворять условию e³1.2:
(рис. 5.19) при условии, что коэффициент перекрытия передачи должен удовлетворять условию e³1.2:
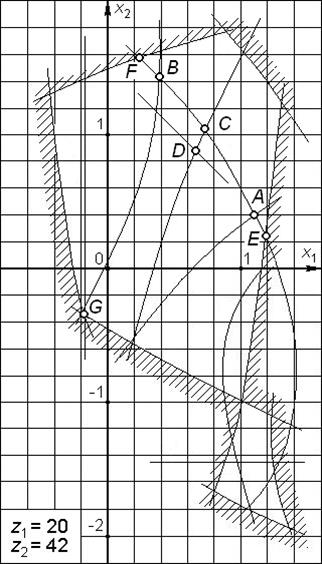 |
| Рис. 5.19 |
· пусть требуется спроектировать передачу с наибольшей изгибной прочностью зубьев при ведущем колесе 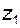 ; таким свойством обладает передача, параметры которой соответствуют точке A;
; таким свойством обладает передача, параметры которой соответствуют точке A;
· наибольшей изгибной прочностью зубьев при ведущем колесе 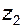 обладает передача, параметры которой соответствуют точке B;
обладает передача, параметры которой соответствуют точке B;
· если требуется спроектировать передачу с износостойкостью, близкой к максимальной, то в качестве коэффициентов смещения для колес этой пары должны быть выбраны координаты точки C;
· передача, соответствующая точке E, обладает наибольшими возможными диаметральными размерами колеса 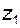 (наибольшим диаметром впадин
(наибольшим диаметром впадин 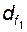 или, что то же самое, наибольшим достижимым коэффициентом смещения
или, что то же самое, наибольшим достижимым коэффициентом смещения  );
);
· передача, для которой  и
и  выбирают по координатам
выбирают по координатам
точки F, имеет наибольшие диаметральные размеры колеса 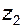 ;
;
· передача, спроектированная по параметрам  и
и  , соответствующим координатам точки G, имеет наибольший коэффициент перекрытия e, достижимый для данной зубчатой пары (и, следовательно, наибольшую плавность зацепления).
, соответствующим координатам точки G, имеет наибольший коэффициент перекрытия e, достижимый для данной зубчатой пары (и, следовательно, наибольшую плавность зацепления).
Отметим, что сделанные замечания к выбору коэффициентов смещения справедливы, если межосевое расстояние передачи не задано и не подлежит округлению.
Учет необходимости округления величины 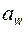 покажем на примере проектирования передачи с износостойкостью, близкой к максимальной:
покажем на примере проектирования передачи с износостойкостью, близкой к максимальной:
- вначале выбираем предварительные значения коэффициентов смещения, как координаты точки C;
- по этим значениям  и
и  с помощью формулы (5.51) находим предварительное значение угла зацепления передачи
с помощью формулы (5.51) находим предварительное значение угла зацепления передачи 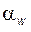 ;
;
- по формуле (5.52) находим межосевое расстояние 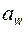 , которое затем округляем в меньшую сторону; в дальнейших расчетах используем округленное значение
, которое затем округляем в меньшую сторону; в дальнейших расчетах используем округленное значение 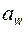 ;
;
- по формуле (5.53) находим угол зацепления, соответствующий округленному значению 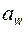 ; найденное здесь значение
; найденное здесь значение 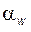 считаем окончательным и используем во всех последующих расчетах;
считаем окончательным и используем во всех последующих расчетах;
- по формуле (5.54) находим значение коэффициента суммы смещений 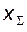 и с его помощью строим на поле БК прямую, соответствующую принятой величине
и с его помощью строим на поле БК прямую, соответствующую принятой величине 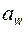 (как это показано на рис. 5.18); в качестве окончательных значений
(как это показано на рис. 5.18); в качестве окончательных значений  и
и  принимаем координаты точки D
принимаем координаты точки D
(рис. 5.19). Как было сказано выше, одну из этих двух величин (например,  ) выбирают на БК, а вторую – рассчитывают (в данном случае
) выбирают на БК, а вторую – рассчитывают (в данном случае 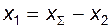 ). Эти значения коэффициентов смещения являются окончательными.
). Эти значения коэффициентов смещения являются окончательными.
Далее выполняется геометрический расчет по формулам (5.55) – (5.62) и проверка качества зацепления по геометрическим показателям (только в учебных расчетах).
5.10. Размеры для контроля взаимного положения разноименных профилей зубьев
(измерительные размеры)
Коэффициент смещения x является важнейшим геометрическим параметром колеса, при нарезании зубьев он обязательно должен контролироваться и притом с достаточной точностью; однако измерить непосредственно этот параметр невозможно.
Для косвенного и в то же время достаточно точного измерения коэффициента смещения используют так называемые измерительные размеры, которые зависят от x и в то же время допускают непосредственное измерение стандартными или специальными средствами.
