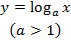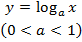Логарифмические уравнения
Логарифмом положительного числа b по основанию 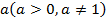 называется показатель степени, в которую надо возвести а, чтобы получить числоb. Обозначается
называется показатель степени, в которую надо возвести а, чтобы получить числоb. Обозначается 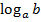 и по определению
и по определению 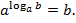
Если основание логарифма а =10 или а = е, то употребляется специальная запись:
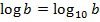 – десятичный логарифм,
– десятичный логарифм,
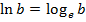 – натуральный логарифм.
– натуральный логарифм.
Функция 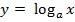 называется логарифмической, она является обратной функцией для показательной функции
называется логарифмической, она является обратной функцией для показательной функции 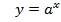 ,
, 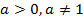 . График логарифмической функции изображен на рис. 4.2.
. График логарифмической функции изображен на рис. 4.2.
|
|
|
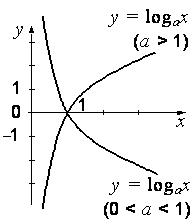
Рис. 4.2. График логарифмической функции.
Свойства логарифмической функции:
1)область определения – множество всех положительных чисел, 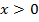 ;
;
2) область значений – множество всех действительных чисел, 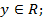
3) если х = 1, то 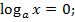
4)если 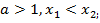 то
то 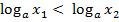 ,
,
где 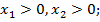
5)если 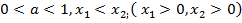 ,
,
то 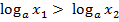 ;
;
6) если 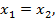 то
то 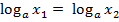
Свойства логарифмов:
1) 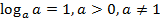 ;
;
2) 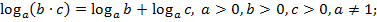
3) 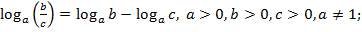
4) 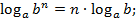
5) 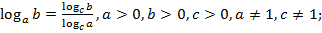
6) 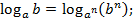
7) 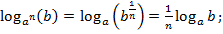
Зная свойства логарифмов, можно выполнять тождественные преобразования.
Пример 1. Вычислить: 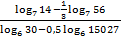
Решение. Применяя формулы 1–4, находим
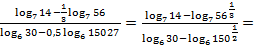
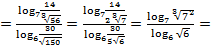
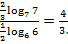
Пример 2. Выразить 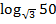 через а и b, если известно, что
через а и b, если известно, что 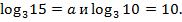
Решение. Используя свойства логарифмов, преобразуем
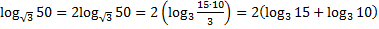 .
.
Пример 3. Вычислить:
15 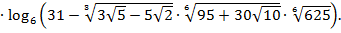
Решение. Так как
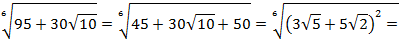
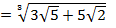 и
и 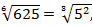
то 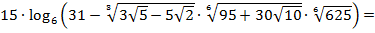
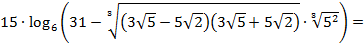
15 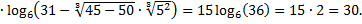
Пример 4. Упростить выражение:
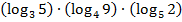
Решение. 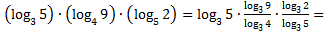
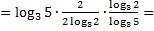 1.
1.
Уравнения, содержащие переменную под знаком логарифма, называются логарифмическими. Простейшие логарифмические уравнения – уравнения вида:
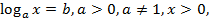 решением которых является
решением которых является 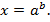
Уравнения вида: 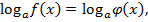 где
где 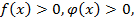 равносильны уравнению
равносильны уравнению 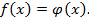 При решении уравнений, содержащих логарифмы в показателе степени, бывает полезно прологарифмировать обе части уравнения по основанию этого логарифма. Следует заметить, что при решении логарифмических уравнений надо указывать область допустимых значений переменной.
При решении уравнений, содержащих логарифмы в показателе степени, бывает полезно прологарифмировать обе части уравнения по основанию этого логарифма. Следует заметить, что при решении логарифмических уравнений надо указывать область допустимых значений переменной.
Пример 5. Решить уравнение:
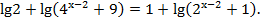
Решение. Область допустимых значений 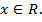 Так как
Так как
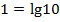 ,то
,то 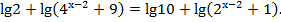
По второму свойству логарифмов,
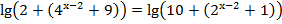
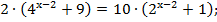
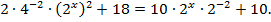
Обозначим 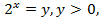 тогда
тогда
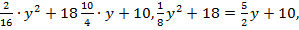
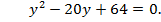
По теореме Виета 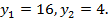
Если 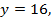 то
то 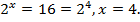
Если 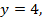 то
то 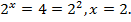
Ответ: 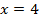 или
или 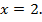
Замечание. При решении показательных и логарифмических уравнений полезно сделать проверку.
Пример 6. Решить уравнение:
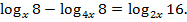
Решение. Областью допустимых значений является решение системы неравенств:
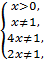 т. е.
т. е. 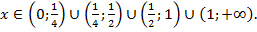
Поскольку 8 и 16 являются степенями двойки, то переходим к логарифмам по основанию 2:
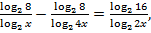
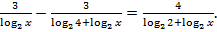
Обозначим 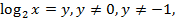 тогда
тогда
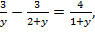
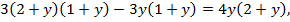
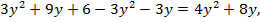
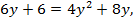
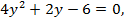
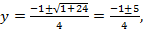
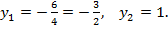
Если 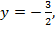 то
то 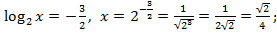
если 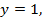 то
то 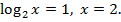
Ответ: 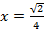 или
или 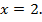
Пример 7. Решить уравнение:
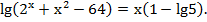
Решение. Областью допустимых значений является множество решений неравенства 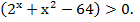 Поскольку решить такое неравенство трудно, то после решения уравнения сделаем проверку и посмотрим, удовлетворяют ли корни уравнения области допустимых значений.
Поскольку решить такое неравенство трудно, то после решения уравнения сделаем проверку и посмотрим, удовлетворяют ли корни уравнения области допустимых значений.
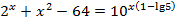
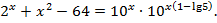
Поскольку 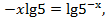 то
то
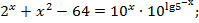
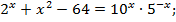
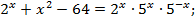
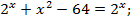
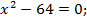
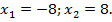
Проверим, принадлежат ли корни области допустимых значений.
Если 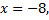 то
то 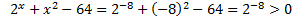
Eсли 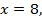 то
то 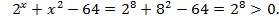 Оба корня удовлетворяют области допустимых значений.
Оба корня удовлетворяют области допустимых значений.
Ответ: 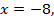 или
или 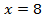 .
.
Пример 8. Решить уравнение: 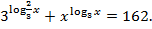
Решение. Область допустимых значений 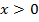 .
.
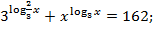
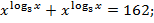
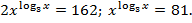
Прологарифмируем обе части равенства по основанию 3:
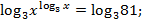
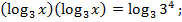
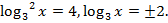
Если 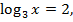 то
то 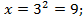
Если 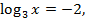 то
то 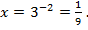
Оба корня удовлетворяют области допустимых значений.
Ответ: 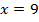 или
или 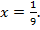
Последующие примеры не являются логарифмическими уравнениями, но содержат логарифмы. Примеры такого рода часто встречаются в вариантах ЕГЭ в частях В и С.
Пример 9. При каких значениях х соответственные значения функций:
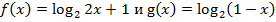 будут отличаться менее чем на 2?
будут отличаться менее чем на 2?
Решение. Для ответа на вопрос требуется решить неравенство: 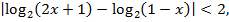 учитывая область допустимых значений уравнения
учитывая область допустимых значений уравнения 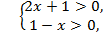 т. е.
т. е. 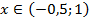 .
.
Раскрывая знак модуля, получим:
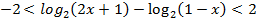 или
или
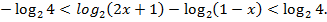
Дальнейшие преобразования приводят к следующим результатам:
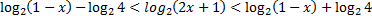
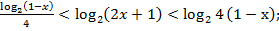
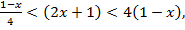 что равносильно системе неравенств
что равносильно системе неравенств 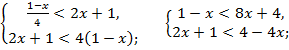
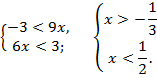
Полученный результат не противоречит области допустимых значений.
Ответ: 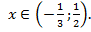
Пример 10. Решите неравенство:
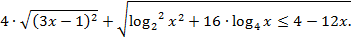
Решение. Прежде всего заметим, что выражение в левой части неравенства неотрицательно, поэтому решение возможно лишь в случае, когда и правая часть неотрицательна, т. е. 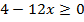 или
или 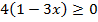 , откуда
, откуда 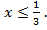
В силу этого 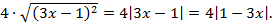 Тогда исходное неравенство приобретает вид:
Тогда исходное неравенство приобретает вид:
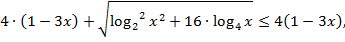 откуда
откуда 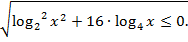
Последнее неравенство может иметь решение в единственном случае, когда 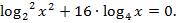
Перепишем уравнение в виде 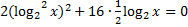
и сделаем замену 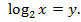
Тогда 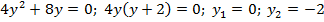 .
.
Если 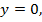 то
то 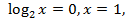 что не удовлетворяет условию
что не удовлетворяет условию  Если
Если 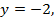 то
то 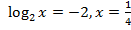 .
.
Ответ: 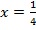 .
.