Исследования на выпуклость вверх и вниз
Определение.Пусть функция 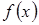 определена и дифференцируема на интервале
определена и дифференцируема на интервале 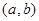 , конечном или бесконечном. Функция
, конечном или бесконечном. Функция 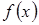 называется выпуклой вниз (вверх) на
называется выпуклой вниз (вверх) на 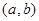 , если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной, абcцисса точки касания которой принадлежит
, если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной, абcцисса точки касания которой принадлежит 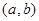 .
.
Исследование функции на выпуклость проводится с использованием второй производной.
Определение.Второй производной 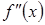 от функции
от функции 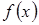 называется производная от первой производной. То есть
называется производная от первой производной. То есть 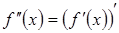 . Производная от второй производной называется производной третьего порядка
. Производная от второй производной называется производной третьего порядка 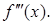 Аналогично определяется производная
Аналогично определяется производная 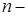 го порядка
го порядка 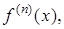 как производная от
как производная от 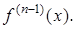
Теорема 1. Если на конечном или бесконечном интервале 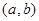 существует
существует 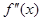 и
и
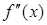 ≥ 0
≥ 0 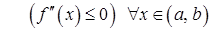 , (1)
, (1)
то функция 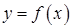 выпукла вниз (вверх) на
выпукла вниз (вверх) на 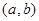 .
.
Замечание.Если неравенства (1) строгие, то график функции 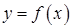 в пределах интервала
в пределах интервала 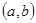 имеет только одну общую точку – точку касания. В таком случае будем говорить, что
имеет только одну общую точку – точку касания. В таком случае будем говорить, что 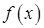 строго выпукла вниз (вверх).
строго выпукла вниз (вверх).
Определение.Точка 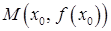 графика функции
графика функции 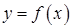 называется точкой перегиба, если существует
называется точкой перегиба, если существует 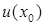 такая, что
такая, что
1) 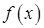 непрерывна в
непрерывна в 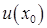 ;
;
2) существует конечное или бесконечное значение 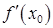 ;
;
3) в 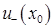 и
и 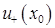 функция
функция 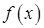 имеет разные направления выпуклости.
имеет разные направления выпуклости.
Замечание.Условие 2) равносильно существованию касательной к графику функции в точке 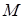 . Если
. Если 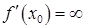 , то в точке
, то в точке 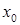 существует вертикальная касательная.
существует вертикальная касательная.
Из определения и теоремы 1 следует следующая теорема о достаточных условиях существования точки перегиба.
Теорема 2.Пусть функция 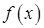 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) 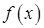 непрерывна в
непрерывна в 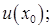
2) существует 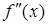 в
в 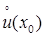 ;
;
3) либо существует 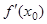 , либо
, либо 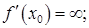
4) 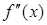 имеет разные постоянные знаки в
имеет разные постоянные знаки в 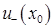 и
и 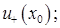
Тогда точка 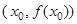 является точкой перегиба графика функции
является точкой перегиба графика функции 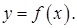
Теорема 3(необходимое условие точки перегиба). Пусть 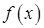 определена в
определена в 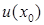 и
и 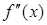 непрерывна в точке
непрерывна в точке 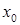 . Если (
. Если ( 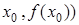 точка перегиба, то
точка перегиба, то 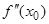 =0.
=0.
Следствие.Если 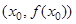 есть точка перегиба, то вторая производная
есть точка перегиба, то вторая производная 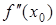 либо не существует, либо равна 0.
либо не существует, либо равна 0.
Замечание.Необходимое условие не является достаточным. Действительно, рассмотрим функцию 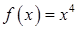 . Очевидно, что
. Очевидно, что 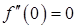 . Однако точка
. Однако точка 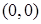 не является точкой перегиба, поскольку
не является точкой перегиба, поскольку 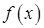 выпукла вниз на всей прямой.
выпукла вниз на всей прямой.
Приведем план исследования функции на выпуклость вверх и вниз и точки перегиба для случая, когда 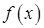 определена на интервале
определена на интервале 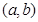 , конечном или бесконечном и
, конечном или бесконечном и 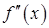 существует и непрерывна везде на
существует и непрерывна везде на 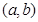 за исключением, быть может, конечного числа точек.
за исключением, быть может, конечного числа точек.
1. Найти корни уравнения 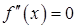 и точки, где
и точки, где 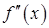 не существует. Пусть это числа
не существует. Пусть это числа 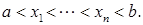
2. Нанести числа 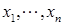 на числовую прямую, на полученных промежутках с помощью пробных точек определить знак
на числовую прямую, на полученных промежутках с помощью пробных точек определить знак 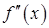 и опираясь на теорему 1 найти направления выпуклости.
и опираясь на теорему 1 найти направления выпуклости.
3. В точках 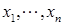 проверить условия теоремы 2 и выбрать среди них точки перегиба.
проверить условия теоремы 2 и выбрать среди них точки перегиба.
Пример.Найти промежутки выпуклости и точки перегиба функции 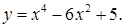
1. Найдем 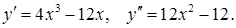 Решим уравнение
Решим уравнение
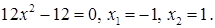
2. Нанесем точки -1, 1 на числовую прямую.
На промежутках 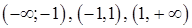 найдем знак
найдем знак 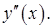 Для этого найдем
Для этого найдем
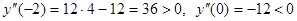 ,
, 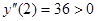 .
.
Согласно теореме 1 функция 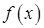 выпукла вниз на лучах
выпукла вниз на лучах 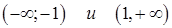 и выпукла вверх на интервале (-1, 1).
и выпукла вверх на интервале (-1, 1).
3. Легко видеть, что в точках –1, 1 выполнены все условия теоремы 2. Найдем 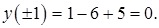 Точки
Точки 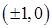 являются точками перегиба.
являются точками перегиба.
В заключение приведем план полного исследования при построении графика функции.
1. Найти область определения.
2. Исследовать функцию на четность, нечетность, периодичность.
3. Найти точки пересечения графика с осями координат.
4. Найти промежутки знакопостоянства.
5. Найти предельные значения функции в граничных точках области определения.
6. Найти асимптоты.
7. Исследовать на непрерывность. Найти точки разрыва и установить характер разрыва.
8. Найти промежутки возрастания, убывания и экстремумы.
9. Найти промежутки выпуклости вверх или вниз и точки перегиба.
10. Вычислить значения функции в нескольких точках и построить график функции.
