Производная и ее приложения
6.2.31–6.2.40.Найти пределы функций, не пользуясь правилом Лопиталя.
6.2.31. а)
lim
3 x ; б)
lim
arctg 3x;
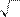
x ® 0
x + 3 -
4
3 - x
x ® 0
sin 5x
æö2x+1
в) lim
3x + 5
; г)
lim
3 - 2x
|
x ® ¥ (2x2 - 1)2
x ® ¥ è 5 - 2xø
6.2.32. а)
lim
x ® 4
x +12 - 4 ; б)
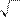x - 2
lim
x ® 0
tg 4 x ;
x + 1 -1
2 + x
2 3 æ ö
|
(2 x + 1) + 3x; г)
lim
5 - 2 x
ç ÷ .
x ® ¥
x3- (2x -1)2
2
x ® 0 è 5 + 3xø
6.2.33. а)
lim
x - 25 ; б)
lim
tgx ;
x ® 5
x - 5
6
x ® 0 sin 2 2x
æö x+3
в) lim
2x - 7
; г)
lim
3x + 1
|
x ® ¥ (x3- 3)(2- x3)
3
x ® ¥ è 3x - 2 ø
6.2.34. а)
lim
x ® -1
x - 7 + 2 ; б)
x + 1
lim
x ® 1
sin( x -1) ;
x 2 - 1
3 æ ö
|
(3x - 2) ; г)
lim
2 - x x
x ® ¥ (x2 + 1)(2- x)
x ® 0
è 2 + x ø
6.2.35. а)
lim
x - 4 ; б)
lim
arcsin x ;
x ® 2
x + 14 - 2
x + 2
x ® 0
3 + x -
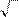2
x2-1
в) lim
( x - 3)(2 - x ) ; г)
lim
æ 2 x + 1 ö
|
x ® ¥
(x -1)3
x ® ¥ çç 2x 2 + 3 ø
3 3
6.2.36. а)
lim
1 + x - 1 - x ; б)
lim
tg 2 x ;
x ® 0 x
x ® 0 5x2 - 9x
4 æ ö
x + 1
в) lim
5x - 6 x + 7 ; г)
lim
2 x + 1
|
|
x ® ¥
(x 2 - 3)2
x ® 0 è
x + 1ø
6.2.37. а)
lim
1 + 2 x - 1 - 3x; б)
lim
sin x ;
x ® 0 5x
x ® 0 arcsin3x
x2+5
в) lim
1 - 2 x - x ; г)
lim
æ 3x + 2 ö
÷
x ® ¥ (2+ x)2- 3x3
x ® ¥ çç 3x 2
.
|
6.2.38. а)
lim
x + 3 ; б)
lim
4 - x - 2 ;
x ® -35
1 - x - 2
4 - 7x
x ® 0
arcsin 2x
2 3 æ ö
|
7 + x + x - 2 x ; г)
lim
x + 2 x
x ® ¥
(1 - x)3
x ® 0 è 3x+ 2 ø
6.2.39. а)
lim
x ® 0
1 + 2 x - 1 - 3x; б)
3x
2 2
lim
x ® p
tg 2 x ;
sin 3x
x+2
æö
в) lim
(x - 3)
+ 5 ; г)
lim
7x + 1
|
x ® ¥ (1- 2x2 )2+ 7
x ® ¥ è 7x - 1 ø
6.2.40. а)
lim
x ® 0
x + x ; б)
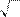
x + 1 - 1
lim
x ® 0
arcsin 2 x;
x + 1 -1
5 æ ö
|
4 + x - x ; г)
lim
7 + x x
x ® ¥ 2 + x 2 - 3x5
x ® 0
è 7 - x ø
6.3.11–6.3.20.Задана функция у=f (х). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
ì x + 4,
|
|
ì x + 2,
|
|
x < -1;
-1 £ x < 1;
x ³ 1.
x £ -1;
-1 < x £ 1;
x > 1.
ì - x,
ï
x £ 0;
6.3.13.f (x) = í- (x -1)2 ,
|
0 < x < 2;
x ³ 2.
ì cosx,
|
|
ì - x,
ï
x £ 0;
0 < x < 1;
x ³ 1.
x £ 0;
6.3.15.f (x) = íx2,
|
ì - x,
|
|
îx - 2,
0 < x £ 2;
x > 2.
x £ 0;
0 < x £ p ;
x > p .
ì- ( x +1),
|
x £ -1;
-1 < x £ 0;
|
ì- x2,
|
|
ì - 2x,
|
|
|
ì- 2 x,
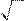ï
x > 0.
x £ 0;
0 < x £ p / 4;
x > p / 4.
x £ 0;
0 < x £ 1;
x > 1.
x £ 0;
6.3.20.f (x) = í x ,
|
0 < x < 4;
x ³ 4.
7.1.1–7.1.10.Найти производные
dyданных функций.
dx
7.1.1. a)
в)
y = arccos
x = 2t 2 + t,
x ;
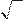y = ln t.
б) y = ln ctg x ;
3
7.1.2. a)
y = x
25 - x2+ 25arccos x ; б)
y = exp (ctg 2x);
в) x =
1 - t ;
1 + t 2
2 5
2 + t 2
y = .
t 2
7.1.3. а)
y = 1 ln
6
x - 3 ;
x + 3
б) y = arcctg [exp(5x)] ;
в) x = sin23t, y = cos23t .
7.1.4. a)
y = ln(x +
x 2 +1); б)
y = 1- cos 3x ; 1+ cos 3x
в) x = t4 + 2t, y = t2 + 5t .
2
7.1.5. a)
y = x x
+1+ arccos 1 ; б)
x 2
y = (x -1)exp (x 2 );
в) x = t – ln sint, y = t + ln cost .
1 2
7.1.6. a)
y = ctg
x + ln sin x;
б) y = exp(cos3x) .
в) x = tg t ,
y = .
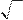
sin2t
7.1.7. a)
y = ln( x -
x - 2 )+
x2- 2x;
б) y = 3x exp(-x-2) ;
в) x = t2 – t3, y = 2t3.
7.1.8. a) y = ln cos2x – ln sin2x ; б) в) x = cos3t , y = sin3t .
x -1
| |
3x ;
7.1.9. a)
y = arccos
; б)
x + 1
y = ln ctg
x + 2 ;
в) x = 3sint, y = 3cos2t .
tg 3 x
ctg 2 x
æ 1 ö
7.1.10. a)
y = -
+ ln sin x; б)
y = x
exp ç ÷;
3 2 è x ø
в) x = 2t – t2 , y = 2t3.
7.2.51–7.2.60.Подобрать соответствующую функцию и найти ее экстремум.
7.2.51. Требуется изготовить из жести ведро цилиндрической формы без крышки данного объема V. Каковы должны быть высота и радиус его дна, чтобы на его изготовление ушло наименьшее количество жести ?
7.2.52. Равнобедренный треугольник, вписанный в окружность радиуса R, вращается вокруг прямой, которая проходит через его вершину параллельно основанию. Какова должна быть высота этого треугольника, чтобы тело, полученное в результате его вращения, имело наибольший объем?
7.2.53. Прямоугольник вписан в эллипс с осями 2a и 2b. Каковы должны быть стороны прямоугольника, чтобы его площадь была наибольшей ?
7.2.54. Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R ?
7.2.55. Найти радиус основания и высоту конуса наименьшего объема, описанного около шара радиуса R ?
7.2.56. При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность ?
7.2.57. Окно имеет форму прямоугольника, завершенного полукругом. Периметр окна равен a. При каких размерах сторон прямоугольника окно будет пропускать наибольшее количество света ?
7.2.58. В точках A и B, расстояние между которыми равно a, находятся источники света соответственно с силами F1и F2. На отрезке AB найти наименее освещенную точку M0.
Замечание. Освещенность точки источником света силой F обратно
пропорциональна квадрату расстояния r ее от источника света:
E = kF / r 2 , k = const.
7.2.59. Из круглого бревна, диаметр которого равен d, требуется вырезать балку прямоугольного поперечного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка наибольшее сопротивление на изгиб ?
Замечание. Сопротивление балки на изгиб пропорционально произведению ширины x ее поперечного сечения на квадрат его высоты y: Q = kxy2 , k = const.
7.2.60. Требуется изготовить открытый цилиндрический бак данного объема V. Стоимость квадратного метра материала, идущего на изготовление дна бака, равна p1руб., а стенок – p2 руб. Каковы должны быть радиус дна и высота бака, чтобы затраты на материал для его изготовления были наименьшими?
7.3.21–7.3.30.Методами дифференциального исчисления: а) исследовать
функцию y = f (x) для
"xÎR
и по результатам исследования построить ее
график; б) Найти наименьшее и наибольшее значения заданной функции на отрезке [a; b].
7.3.21. а)
y = 4 x
|
б) [–3; 3] .
7.3.22. а)
x 2 - 1
y = ,
x 2 + 1
б) [–1; 1] .
7.3.23.
| |
y = x ,
б) [–2; 2 ] .
7.3.24. а)
x 2 + 1
x 2 - 5
y = ,
б) [–2; 2] .
x - 3
7.3.25. а)
2 - 4x2
y = 1 - 4x2 ,
б) [ 1; 4] .
7.3.26. а)
y = (x -1)e3x+1,
б) [ 0; 1] .
7.3.27. а)
y = ln 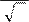x ,
x
б) [ 1; 9] .
7.3.28. а)
y = e 2-x ,
б) [–1; 1] .
7.3.29. а)
y = xe
- x 2 ,
б) [–2; 2] .
7.3.30. а)
x2- 3
|
|
б) [–2; 2] .
x + 9