Расчет степени устойчивости модели

Нейтральная центровка самолёта Хтн (граница за которой самолёт станет неустойчивым) приблизительно равна:

Х_тн = 0,2 + 0,3А_го = 0,2 + 0,3·1,205 = 0,708, где А_го - мощность горизонтального оперения определяется по формуле:

А_го = S_го·L_го/(S·В_сах) = 0,062884·0,9/(0,288·0,163) = 1,205

Sго – площадь горизонтального оперения

Всах – величина средней аэродинамической хорды крыла (САХ)

Lго – плечо горизонтального оперения отсчитывается от 25% САХ до четверти хорды горизонтального оперения

S – площадь крыла

Продольную устойчивость модели упрощённо можно охарактеризовать степенью продольной статической устойчивости по перегрузке (для простоты назовем степенью устойчивости):

Z = Хт – Xтн

где: Z- для устойчивого самолета величина всегда отрицательная

Хт – положение центра тяжести в долях хорды. Согласно чертежу при полете положение центра тяжести находится на 60% САХ, т.е. Хт = 0,6

Z = 0,6 – 0,708 = -0,108, т.к Z < 0, следовательно модель устойчива.

Построение двумерной имитационной модели движения ЛА

Соберём двумерную имитационную модель движения ЛА в программном пакете Matlab/Simulink:

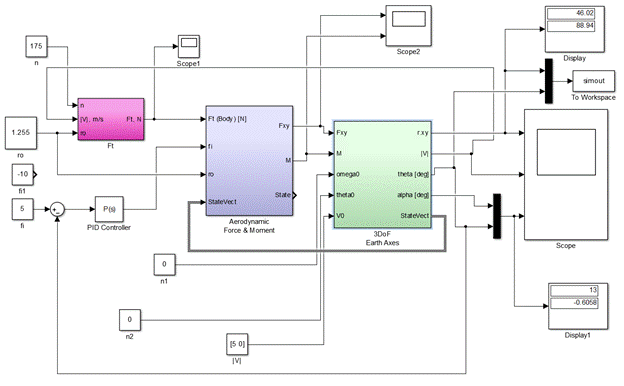
Рис.11. Двумерную имитационную модель движения ЛА

Первый блок (subsystem) раскрывает формулу тяги винта, и следовательно, на выходе мы получаем значение силы тяги винта.

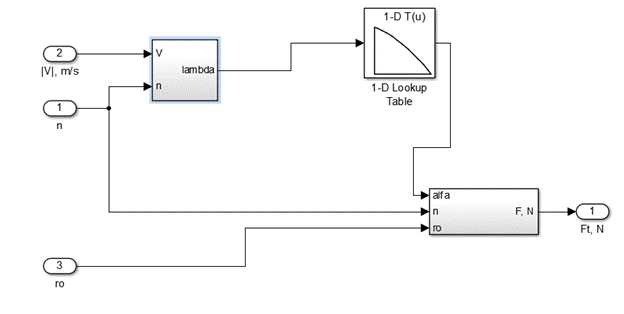
Рис.12. Первый блок имитационной модели движения ЛА

Второй блок раскрывает уравнение моментов:

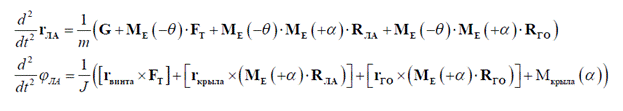
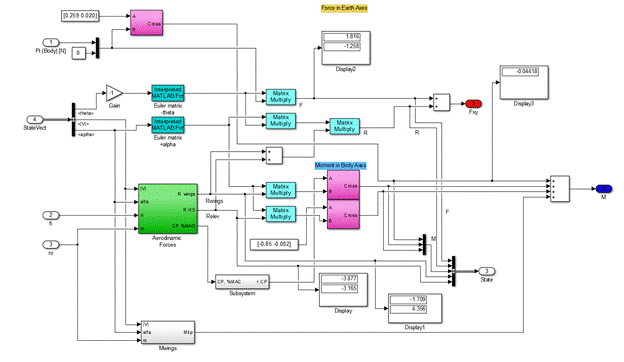
Рис.13. Второй блок имитационной модели движения ЛА

Второй блок включает подблок (subsystem), который обозначен Aerodynamic Forces. Данный подблок учитывает аэродинамические характеристики самолета.

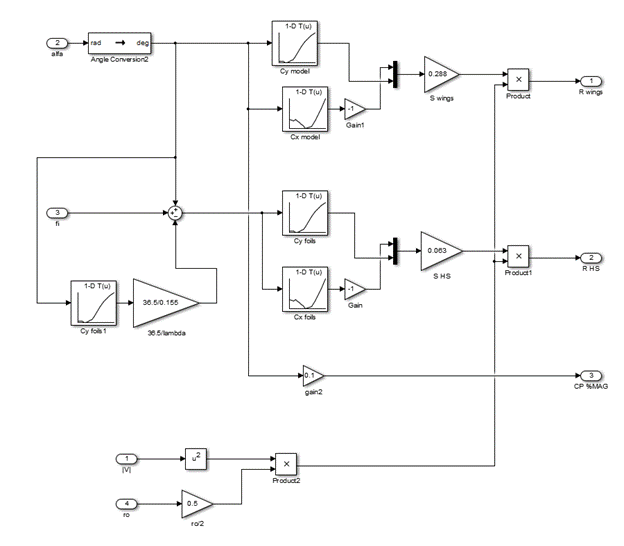
Рис.14. Подблок второго блока имитационной модели движения ЛА

Третий блок описывает уравнения движения ЛА:

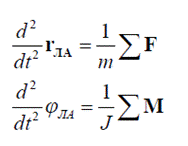
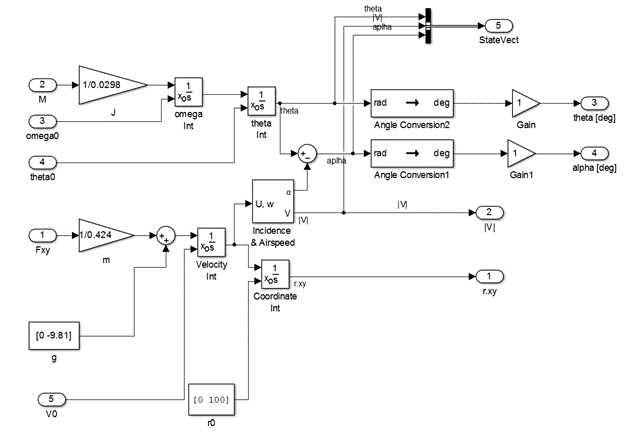
Рис.14. Третий блок имитационной модели движения ЛА.

Полученные характеристики в результате работы данной модели:

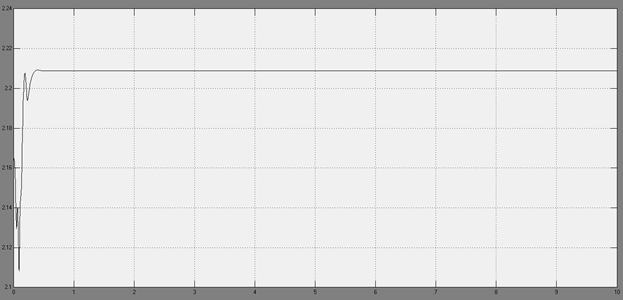
Рис.15.Зависимость силы тяги винта от времени.

Рис.16.1)Зависимость координат (х –фиолетовый цвет, y – черный) результирующей силы от времени;

2)Зависимость результирующего момента от времени соответственно.

По графику видно, что результирующий момент сводится к 0.

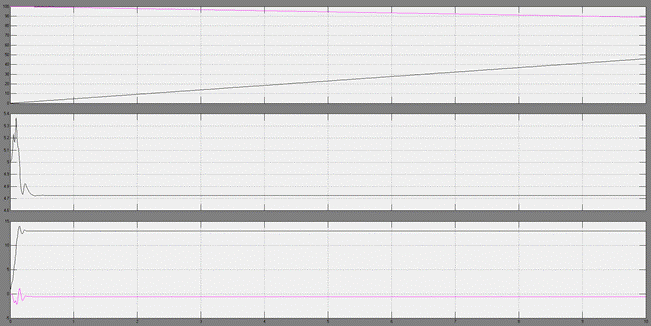
Рис.17. 1)Зависимость координат самолета (y –фиолетовый цвет, x – черный) от времени;

2) Зависимость скорости самолета от времени

3) Зависимость углов альфа (черный) и тетта (фиолетовый) от времени

Выводы

При создании системы управления самолета F-1-C были получены следующие характеристики самолета: сила тяги винта, высота, скорость, сумма сил и моментов, угол тангажа, угол атаки. Самолет планирует постепенно медленно снижает высоту во время полета, при этом при заданных углу тангажа и атаки он стабилизируется по скорости и сохраняет ее на протяжении всего полета. Также сумма сил и моментов, действующих на самолет будет равна 0. Также в данной модели была осуществлена обратная связь по тангажу с применением P-регулятора.