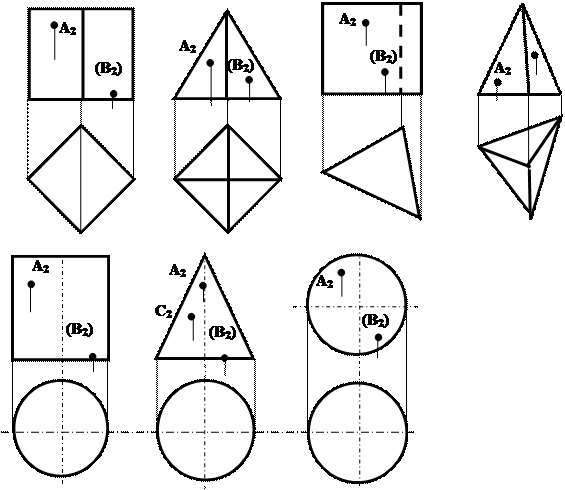
Задачи для самостоятельного решения. (B2) Задача 1
 |
|
Рис.7.7
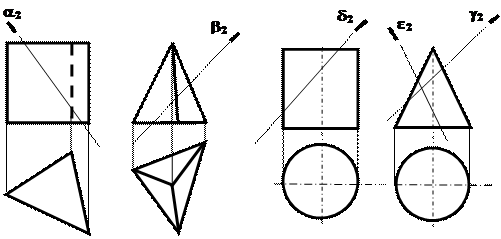Задача 2. Построить отсеченную часть геометрического тела натуральную величину сечения (рис.7.8).
Рис. 7.8
Задача 3. Построить геометрическое тело в трех проекциях (рис.6.9).
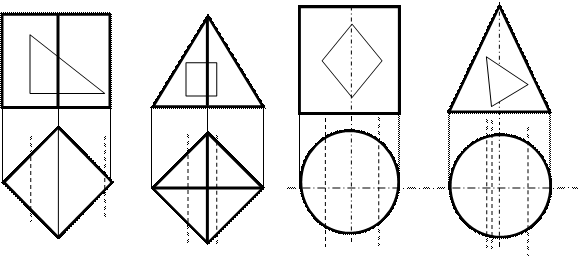
Рис.79
ЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ
Общие теоретические положения
Линия пересечения двух поверхностей в общем виде представляет собой пространственную кривую, которая может распадаться на две части и более. Обычно линию пересечения поверхностей строят по отдельным точкам. Сначала определяют опорные точки в пересечении контурных линий каждой поверхности с другой. Опорные точки позволяют видеть, в каких пределах расположены проекции линии пересечения и где между ними имеет смысл определить промежуточные точки. При этом нужно иметь ввиду, что проекции линии пересечения всегда располагаются в пределах площади наложения одноименных проекций пересекающихся поверхностей.
Общим способом построения точек линии пересечения двух поверхностей является метод вспомогательных секущих плоскостей. Суть метода состоит в следующем. Вводятся вспомогательные секущие проецирующие плоскости. Вспомогательная плоскость пересекает данные поверхности по линиям (желательно, графически наиболее простым). В пересечении этих линий получаются точки, принадлежащие обеим поверхностям, т.е. точки их линии пересечения.. Секущие плоскости обычно выбираются частного положения.
Примеры решения задач
Задача 1. Построить линию пересечения поверхности конуса и сферы методом вспомогательных секущих плоскостей (рис.8.1).
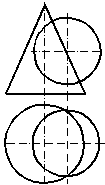Дано:
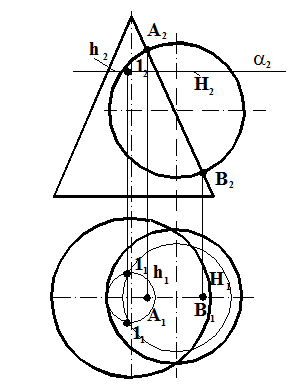
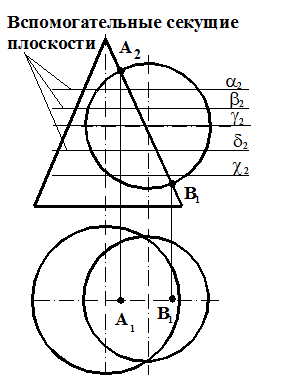Решение:
Рис.91.
Рис.8.1
 |
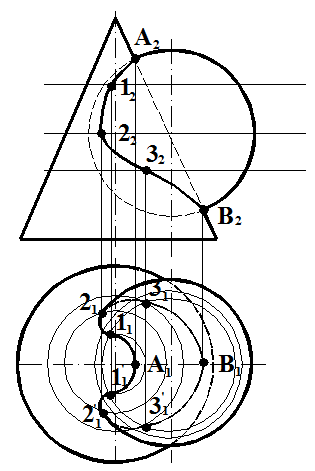Рис.8.1 (продолжение)
Задачи для самостоятельного решения
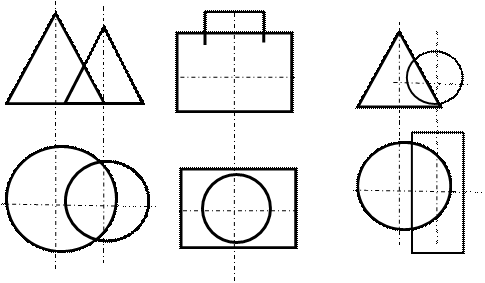
Задача 1. Построить линию пересечения двух поверхностей вращения (рис.8.2).
ЛИТЕРАТУРА
1. Гордон О.В., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.:Наука, 1977.
2. Гордон О.В., Иванов Ю.В., Солнцева Т.Е. Сборник задач по курсу начертательной геометрии. М.:Наука, 1977.
3. Егоров В.В. Задачи по инженерной графике. Л.: Изд. ЛКИ, 1983.
4. Егоров В.В. Методические указания к выполнению заданий по начертательной геометрии и техническому черчению. Л.: Изд. ЛКИ, 1983.
5. Лагерь А.И., Колесникова Э.А. Инженерная графика. М.:Высшая школа, 1985.
6. Бубенников А.В. Начертательная геометрия. Задачи для упражнений. М.: Высшая школа, 1981.
7. Методические указания по дисциплине «Начертательная геометрия и инженерная графика» Часть 2 «Инженерная графика». – Северодвинск: РИО Севмашвтуза. – 2005. – 54 с.
Приложение 1
Пример выполнения эпюра № 1
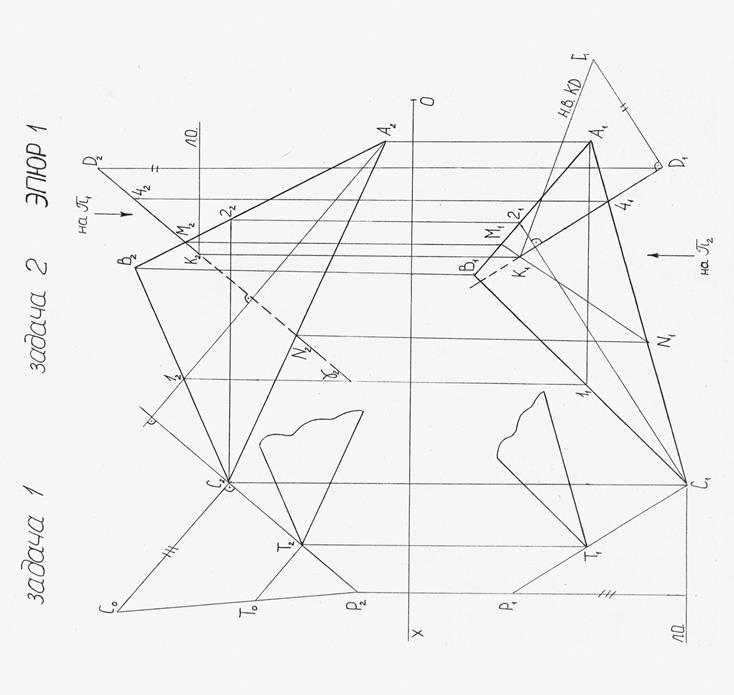
Приложение 2
Пример выполнения эпюра № 2
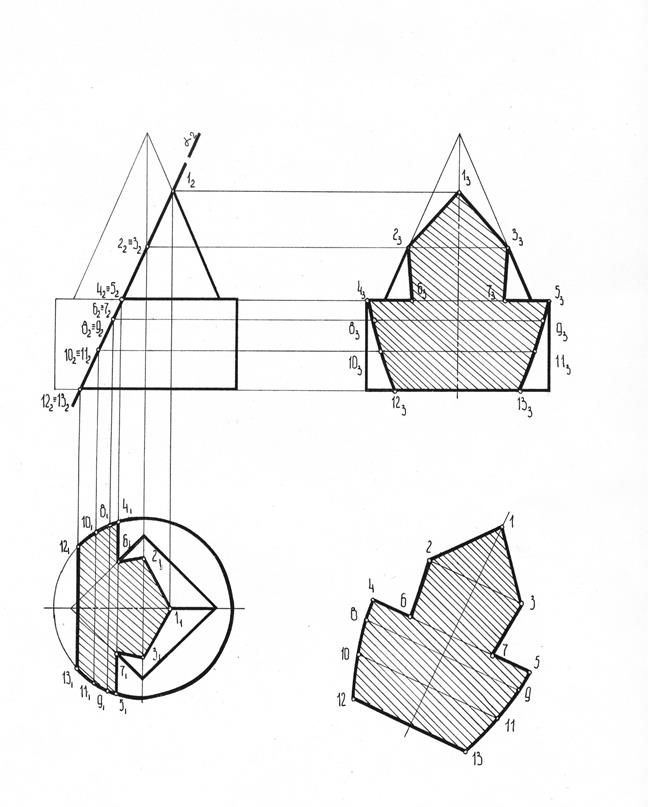
Кремлева Людмила Викторовна
Методические указания по дисциплине «Начертательная геометрия и инженерная графика
Часть 1 «Основы начертательной геометрии»
Редактор
Корректор
Компьютерный набор Кремлева Л.В.
Лицензия Код 221 Серия ИД № 01734
от 11 мая 2000 года
Сдано в производство 20.06.2005.Подписано в печать 28.06.2005.
Формат 60´80/16. Бумага типографская Усл.печ. 3,3 . Заказ № 147 .
Тираж 30 экз. Темплан 1999 г. Изд. № 246
| Редакционно-издательский отдел Севмашвтуза |
| 164500, г. Северодвинск, ул. Воронина, 6 |