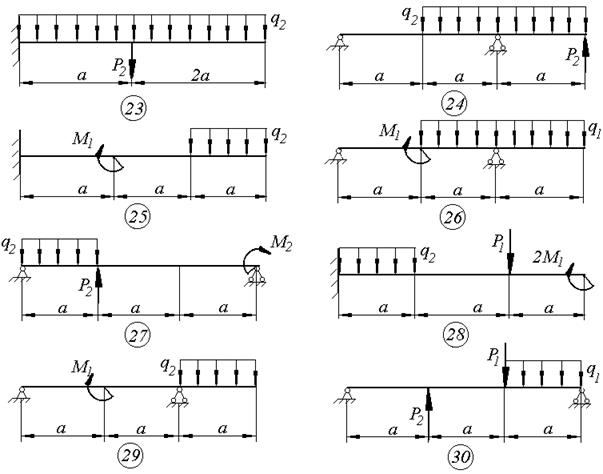
Задача 4. плоский изгиб балки
Для консольной, либо шарнирно опёртой балки (см. схемы к задаче 4), нагруженной изгибающими моментами и поперечными нагрузками необходимо:
1. Определить опорные реакции.
2. Составить аналитические выражения для внутренних силовых факторов (поперечных сил и изгибающих моментов) на всех участков балки.
3. По полученным зависимостям построить эпюры поперечных сил и изгибающих моментов.
4. Из условия прочности по нормальным напряжениям подобрать размеры поперечных сечений балки для трёх вариантов:
а) двутавр;
б) круг;
в) прямоугольник, с соотношением сторон h/в=2.
Численные значения приведены в таблице 2.1.
Таблица 2.1
| № | Р1, кН | Р2, кН | q1, кН/м | q2, кН/м | М1, кНм | М2, кНм |
| 10 | 80 | 10 | 70 | 15 | 90 | |
| 20 | 70 | 15 | 80 | 25 | 80 | |
| 30 | 60 | 20 | 90 | 35 | 70 | |
| 40 | 50 | 25 | 60 | 45 | 50 | |
| 50 | 40 | 30 | 50 | 55 | 40 | |
| 60 | 30 | 35 | 40 | 65 | 30 | |
| 70 | 10 | 40 | 30 | 75 | 20 | |
| 80 | 20 | 45 | 20 | 85 | 50 | |
| 10 | 50 | 55 | 50 | 95 | 10 | |
| 20 | 70 | 65 | 20 | 90 | 30 |
Принять для всех балок следующие соотношения: а=1м;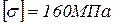 
.
Схемы к задаче 4
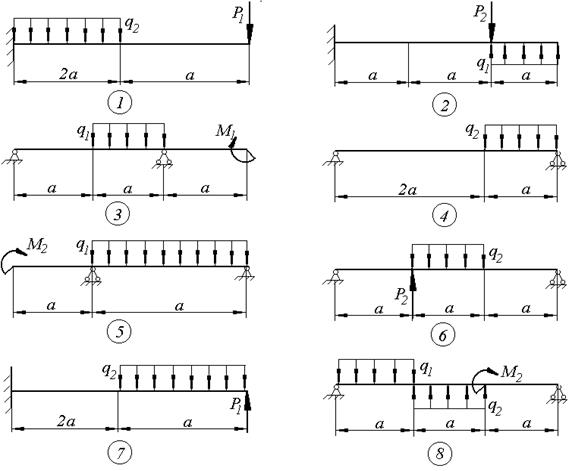
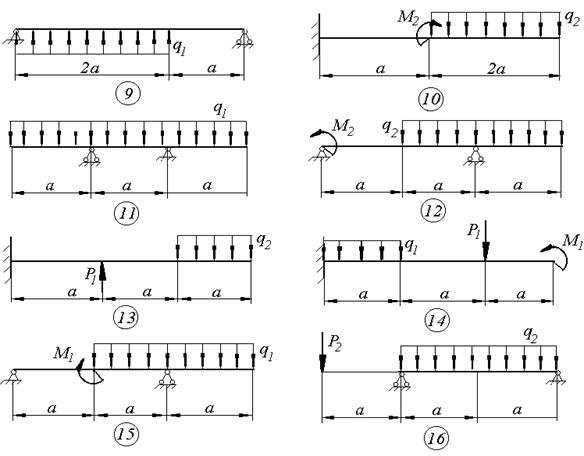
Схемы к задаче 4
Пример решения задачи 4
Для балки работающей на изгиб (рис. 2.1,а) необходимо:
1. Определить значение поперечной силы Q и изгибающего момента М, построить соответствующие эпюры.
2. Подобрать размеры поперечного сечения балки из условия прочности по допускаемым напряжениям на изгиб для 3-ёх вариантов:
а) двутавра;
б) прямоугольного поперечного сечения со сторонами b и h при соотношении h/b=2;
в) круглого поперечного сечения.
Дано: М=10 кН×м; Р=10 кН; q1=50кН/м; а=1м; в=1м; с=1м; .
Решение
1. Опорные реакции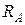 
и 
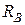(рис. 2.1,б) направим вверх. На балку не действуют горизонтальные силы, поэтому на опоре А будет только вертикальная реакция. Для определения реакций опор составим 2 уравнения равновесия:
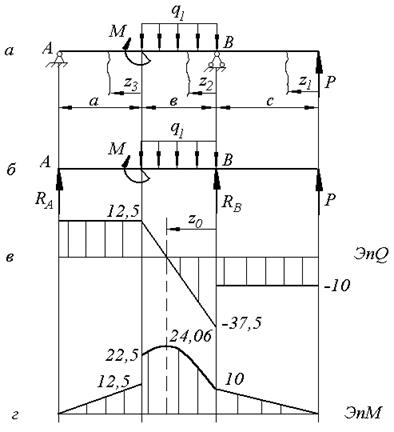
Рис. 2.1 Схема и эпюры внутренних усилий к примеру решения задачи4
;
.
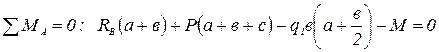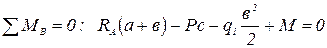Из этих уравнений определим реакци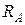и и :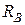
; 
.
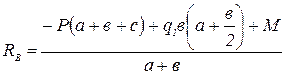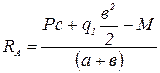После подстановки численных значений получим: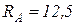 
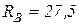кН; 
кН.
Дополнительное уравнение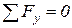 
можно использовать для проверки полученного результата:
;
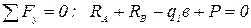12,5+27,5-50+10=0;
2. В поперечных сечениях балки возникают изгибающие моменты М и поперечные силы Q.
При решении задачи используем правило знаков внутренних усилий: поперечная сила Q в сечении положительна, если равнодействующая внешних сил стремится повернуть рассматриваемую часть по часовой стрелке относительно центра тяжести сечения.
Изгибающий момент М в сечении будем считать положительным, если балка изгибается таким образом, что растянутые волокна находятся в нижней части балки, а сжатые – в верней части.
Разобьём балку на 3 силовых участка. Границами участков являются сечения, к которым приложены сосредоточенные моменты и силы, а также конец и начало распределённой нагрузки.
Первый участок: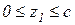 
.
Составим аналитические выражения для определения величины поперечной силы и момента, используя метод сечений и учитывая правило знаков.
;
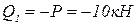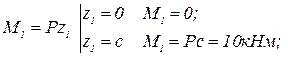
Второй участок: 
.
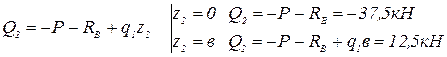
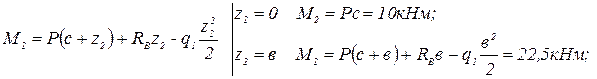
Эпюрой изгибающего момента на 2-ом участке является квадратная парабола (рис.2.1,г). Поэтому для её построения надо знать координаты трёх точек: в начале, в конце участка и в точке, где эпюра имеет экстремум. Экстремум на параболе будет в том же сечении балки, в котором поперечная сила Q равна нулю. Расстояние до сечения, в котором на эпюре момента будет экстремум, обозначим через z0. Значение z0 найдём из следующего уравнения:
.
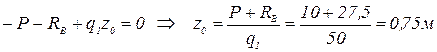Подставим значение z0 в уравнение для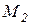 
и найдём экстремум на параболе.
.
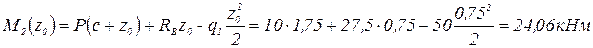Третий участок: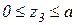 
.
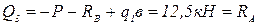
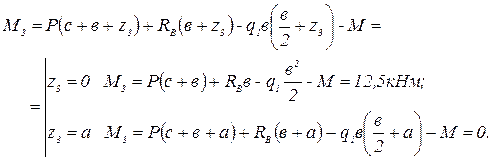
По найденным значениям Q и М строим эпюры поперечной силы (рис.4,в) и изгибающего момента (рис.2.1,г).
3. Из условия прочности балки по нормальным напряжениям подберём размеры поперечного сечения балки для 3-ёх вариантов.
Опасным сечением является сечение балки, проходящее через экстремум на параболе, т.к. в этом сечении будет наибольший изгибающий момент по абсолютной величине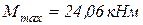 
. Из условия прочности:
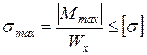
для стальной балки определим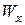 
:
.
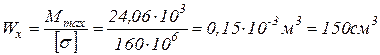а) По найденному значению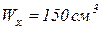 
подберём номер двутавра по ГОСТ 8239-72. Ближайшая величина момента сопротивления 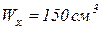, что соответствует двутавру № 18а .
б) Для прямоугольного поперечного сечения момент сопротивления сечения имеет следующую зависимость: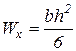 
, при отношении h/b=2 будем иметь: 
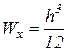, откуда высота сечения 
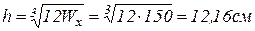, а ширина сечения b=h/2=6,08 см .
в) Для круглого поперечного сечения момент сопротивления сечения следующий: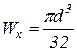 
.
Из этого выражения определим диаметр: 
.
Кручение вала
Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор - крутящий момент Mк.
Брусья, передающие крутящий момент называются валами.
Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. В местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.
Условие прочности при кручении формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде
.
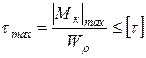Величина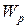 
называется моментом сопротивления сечения при кручении или полярным моментом сопротивления сечения
Для сплошного круглого сечения
.
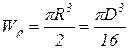Для кольцевого сечения
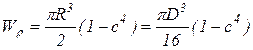, где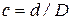 
.
Из условия прочности можно определить диаметр вала:
- для сплошного сечения
,
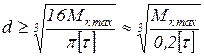- для кольцевого сечения
,
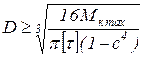