Центральные и вписанные углы

Дуга – часть окружности.

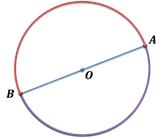
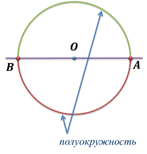
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.

Угол с вершиной в центре окружности называется центральным углом.

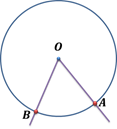
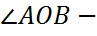центральный угол

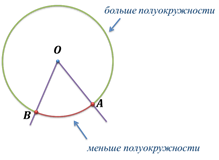
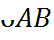Если окружности меньше полуокружности или является полуокружностью, то ее градусная мера равна градусной мере .

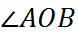Если 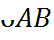больше полуокружности, то ее градусная мера считается равной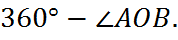

Вписанный угол 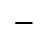угол, вершина которого лежит на окружности, а стороны пересекают окружность.

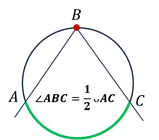
Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается.

« »

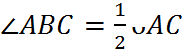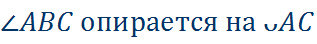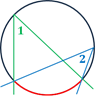
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность прямой.

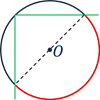
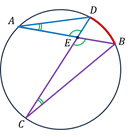Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

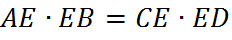
Четыре замечательные точки треугольника

Замечательные точки треугольника– это точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.

Свойства точки, лежащей на биссектрисе неразвернутого угла:

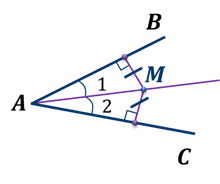
Теорема. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

Обратная теорема. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Теорема. Биссектриса неразвернутого угла есть геометрическое место точек, равноудаленных от сторон данного угла.

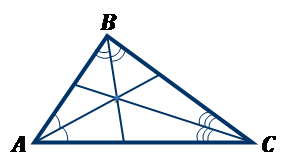
Биссектрисы треугольника пересекаются в одной точке.

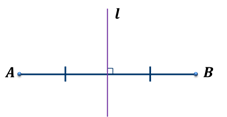Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Свойства точки, лежащей на серединном перпендикуляре к отрезку:

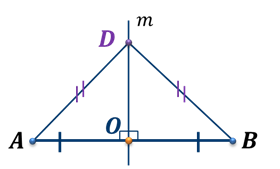Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Теорема. Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.

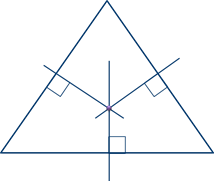
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Медианы треугольника пересекаются в одной точке.

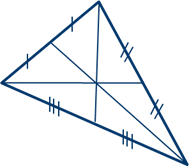
Высоты треугольника (или их продолжения) пересекаются в одной точке.

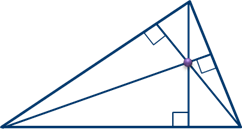
Вписанная и описанная окружности

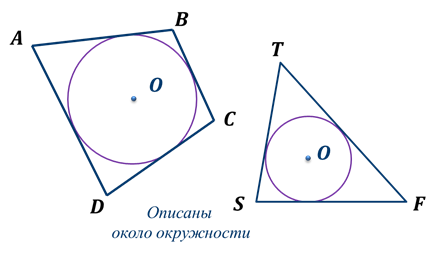Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

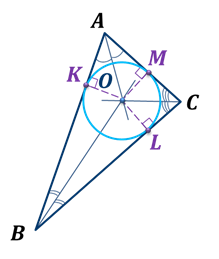
Теорема. В любой треугольник можно вписать окружность.

Замечания.

1. В треугольник можно вписать только одну окружность.

2. В отличие от треугольника не во всякий четырехугольник можно вписать окружность.

Если в четырехугольник можно вписать окружность, то его стороны обладают следующим замечательным свойством:

В любом описанном четырехугольнике суммы противоположных сторон равны.

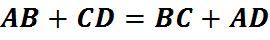
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

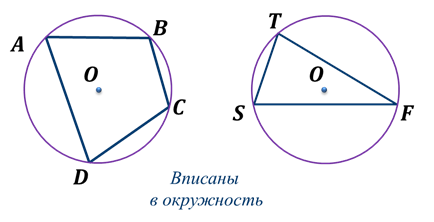
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Теорема. Около любого треугольника можно описать окружность.

Замечания.

1. Около любого треугольника можно описать только одну окружность.

2. В отличие от треугольника около четырехугольника не всегдаможно описать окружность.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна .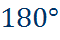

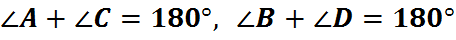
Если сумма противоположных углов четырехугольника равна 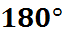, то около негоможно описать окружность.

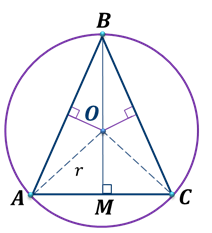
Перпендикуляры, восстановленные к серединам сторон треугольника (серединные перпендикуляры) пересекаются в одной точке, которая является центром описанной окружности, и называется ортоцентром.

Оглавление

Многоугольники. 2

Параллелограмм и трапеция. 6

Прямоугольник, ромб, квадрат. 9

Площадь многоугольника. 13

Площади параллелограмма, треугольника и трапеции. 14

Теорема Пифагора. 16

Определение подобных треугольников. 18

Признаки подобия треугольников. 20

Применение подобия к доказательству теорем и решению задач. 22

Соотношения между сторонами и углами прямоугольного треугольника. 24

Касательная к окружности. 26

Центральные и вписанные углы.. 28

Четыре замечательные точки треугольника. 30

Вписанная и описанная окружности. 33