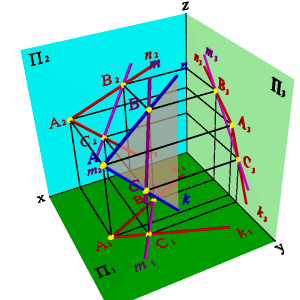
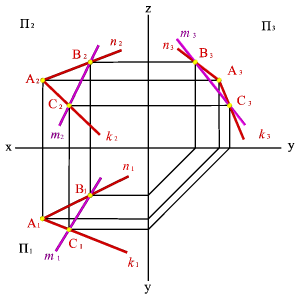
Задача. Дана плоскость (n,k) и одна проекция прямой m2.

Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m₂ пересекает прямые n и k в точках В₂ и С₂, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k.

Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

			а) модель		б) эпюр
Рисунок 5.14. Прямая и плоскость имеют две общие точки

Аксиома 2.Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.5.15).

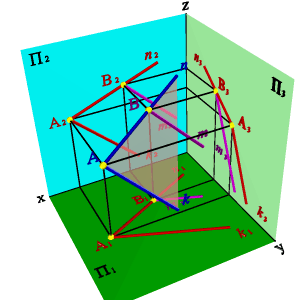
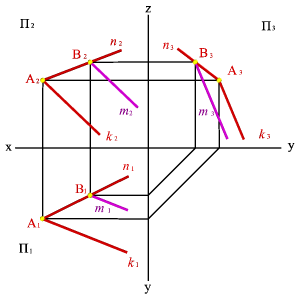
Задача.

Через точку В провести прямую m если известно, что она принадлежит плоскости заданной пересекающимися прямыми n и k.

Пусть В принадлежит прямой n лежащей в плоскости заданной пересекающимися прямыми n и k. Через проекцию В₂ проведем проекцию прямой m₂ параллельно прямой k₂, для нахождения недостающих проекций прямой необходимо построить проекцию точки В₁, как точки лежащей на проекции прямой n₁ и через неё провести проекцию прямой m₁ параллельно проекции k₁.

Таким образом точки В принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эту точку и параллельна прямой k, значит согласно аксиоме прямая принадлежит этой плоскости.

	а) модель		б) эпюр
Рисунок 5.15. Прямая имеет с плоскостью одну общую точку и параллельна прямой расположенной в этой плоскости

Главные линии в плоскости

Среди прямых линий, принадлежащих плоскости, особое место занимают прямые, занимающие частное положение в пространстве:

1. Горизонтали h - прямые, лежащие в данной плоскости и параллельные горизонтальной плоскости проекций (hÎСВА, hP₁, h₂Ох,h₃Оy)(рис.5.16).

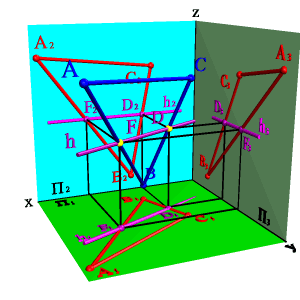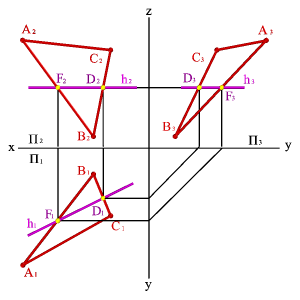	а) модель		б) эпюр
Рисунок 5.16. Горизонталь

2. Фронтали f - прямые, расположенные в плоскости и параллельные фронтальной плоскости проекций (fÎСВА, fP₂, f₁Ох, f₃Оz)(рис.5.17).

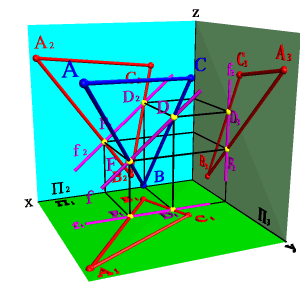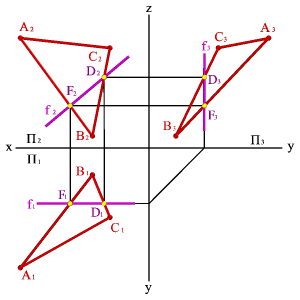	а) модель		б) эпюр
Рисунок 5.17. Фронталь

3. Профильные прямые р - прямые, которые находятся в данной плоскости и параллельны профильной плоскости проекций (рÎСВА, рP₃, р₁^Ох, р₂^Ох)(рис.5.18).

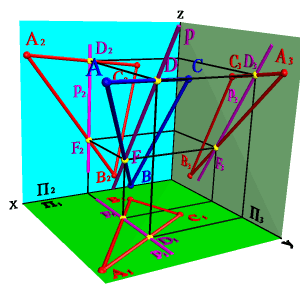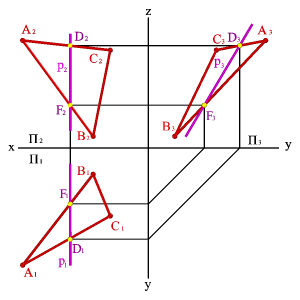	а) модель		б) эпюр
Рисунок 5.18. Профильная прямая

Следует заметить, что следы плоскости можно отнести тоже к главным линиям. Горизонтальный след - это горизонталь плоскости, фронтальный - фронталь и профильный - профильная линия плоскости.

4. Линия наибольшего ската и её горизонтальная проекция образуют линейный угол j , которым измеряется двугранный угол, составленный данной плоскостью и горизонтальной плоскостью проекций (рис.5.19).

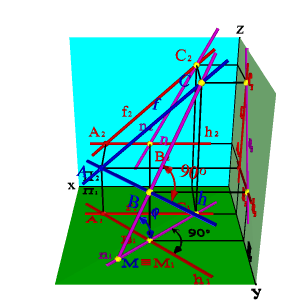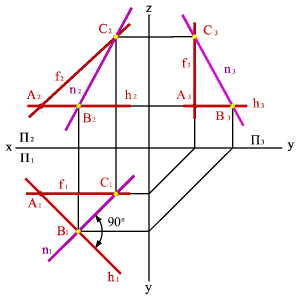	а) модель		б) эпюр
Рисунок 5.19. Линия наибольшего ската

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Прямая линия, параллельная плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскостии не принадлежит этой плоскости.

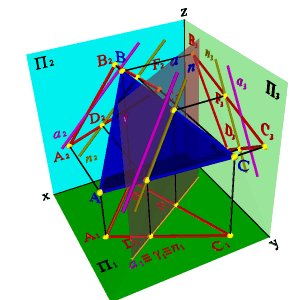
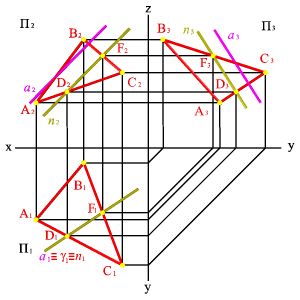
Задача. Дано: проекции плоскости общего положения ABC и прямой общего положения а.

Требуется оценить их взаимное положение (рис.5.20).

	а) модель		б) эпюр
Рисунок 5.20. Прямая параллельная плоскости

Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостейg и АВС- прямую п (DF). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а₁ и со следом плоскости g. Проекция прямой п₂ параллельна а₂, п₃ параллельна а₃, следовательно, прямая а параллельна плоскости AВС.

Прямая линия, пересекающая плоскость

Нахождение точки пересечения прямой линии и плоскости – основная задача начертательной геометрии.