R – перпендикулярная к оси вращения составляющая r’

3) силы, действующие на тело, движущееся во вращающейся системе отсчета (рис. П 1. 17):

F_к=2m×[v^’ ω],

где F_к – сила Кориолиса;

v^’ – скорость движения тела;

w – угловая скорость вращающейся системы отсчета.

Основной закон динамики для неинерциальных систем отсчета:

ma^’=F+F_ин+F_ц +F_к,

где F, F_ин, F_ц, F_к – ранее рассмотренные силы, действующие в неинерциальных системах отсчета.

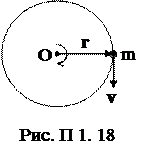Основная задача динамики вращательного движения – нахождение угловых ускорений, сообщаемых известными силами.

Момент инерции – скалярная физическая величина, характеризующая инертность тела при вращательном движении.

Момент инерции материальной точки относительно неподвижной оси вращения – физическая величина, равная произведению массы материальной точки на квадрат расстояния до оси или центра вращения (рис. П 1. 18):

DI=Dm×r².

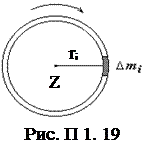
Момент инерции тела относительно оси z – физическая величина, равная сумме моментов инерции отдельных материальных точек тела относительно той же оси вращения (рис. П 1. 19):

; ,

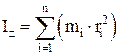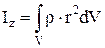где m_i – масса i – й точки;

r_i – расстояние i – й точки до оси z;

ρ – плотность вещества, из которого состоит тело;

V – объем тела.

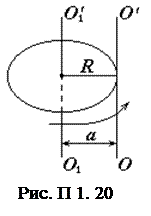
Теорема Штейнера – момент инерции тела относительно произвольной оси z равен сумме момента инерции того же тела I₀ относительно оси, параллельной данной и проходящей через центр масс, и произведения массы тела m на квадрат расстояния между осями (а):

I_z=I₀+mа².

На рисунке П 1. 20 представлено применение теоремы Штейнера к расчету момента инерции диска относительно оси ОО^' параллельной оси О₁О₁^'.

Главные оси инерции – три взаимно перпендикулярных свободных оси вращения тела произвольной формы, проходящие через его центр масс.

Момент импульса материальной точки относительно неподвижной оси вращения (L) – векторная физическая величина, модуль которой равен произведению модуля импульса на плечо (рис. П 1. 21):

çLê=êpê×l.

В векторной форме

L=[r´p]=[r´mv],

где m – масса материальной точки;

v – скорость материальной точки;

l – плечо (кратчайшее расстояние от направления импульса до оси вращения).

Момент импульса системы относительно неподвижной оси вращения z –проекция на эту ось вектораL (момента импульса системы):

,

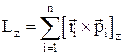где r_i, p_i – радиус – вектор и импульс i – й материальной точки;

n – общее число точек в системе.

Связь момента импульса тела с вектором угловой скорости ω и моментом инерции:

L=Iω.

Момент силы относительно центра вращения или неподвижной оси вращения – векторная физическая величина, модуль которой равен произведению модуля силы на плечо (рис. П 1. 22):

çMç=çFçl,

где l – плечо силы – кратчайшее расстояние от линии действия силы до центра вращения.

В векторной форме

M=[r´F].

Главный или результирующий момент сил относительно неподвижной оси вращенияравен векторной сумме моментов слагаемых сил:

.
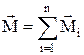