Основные теоретические сведения. Практическое занятие № 1
Практическое занятие № 1
Основы работы с MATLAB
Цель занятия: изучение интерфейса пользователя системы MATLAB и основ работы с системой в режиме прямых вычислений.
Основные теоретические сведения
Исторически MATLAB разрабатывался как диалоговая среда для матричных вычислений (MATrix LABoratory). Со временем пакет был оснащен хорошей графической системой, дополнен средствами компьютерной алгебры от Maple и усилен библиотеками команд (или Toolboxes), предназначенными для эффективной работы со специальными классами задач.
В состав MATLAB входят интерпретатор команд, графическая оболочка, редактор-отладчик, библиотеки команд, компилятор, символьное ядро пакета Maple для проведения аналитических вычислений, математические библиотеки MATLAB на C/C++, генератор отчетов и богатый инструментарий (Toolboxes).
Интерфейс MATLAB вполне отвечает современным канонам (см. рисунок 1.1). Он многооконный и имеет ряд средств прямого доступа к различным компонентам системы. Следует обратить внимание на следующие кнопки панели инструментов:
New M-file — выводит пустое окно редактора m-файлов;
Open file — открывает окно для загрузки файлов Matlab;
Simulink — открывает окно браузера библиотек Simulink;
Help — открывает окно справки.
Эти функции дублируются в очень простом меню системы MATLAB.
В левой части окна системы появились окна со вкладками Launch Pad/Workspace доступа к компонентам системы и вкладками текущей директории Current Directory и истории сессии History. Они обеспечивают оперативный контроль за состоянием системы. Выводимые на экран окна интерфейса MATLAB могут быть включены или отключены из пункта меню View.
Вся работа организуется через командное окно (Command Window), которое появляется при запуске программы. В процессе работы данные располагаются в памяти (Workspace) в виде матриц.
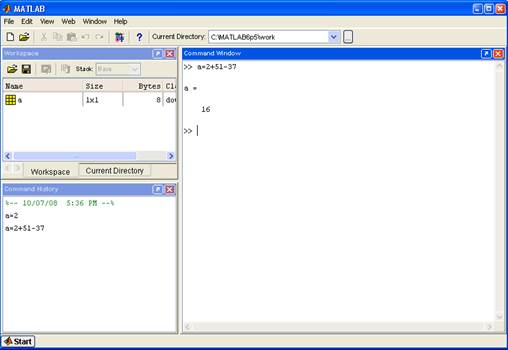
Рисунок 1.1 – Интерфейс программы Matlab
Все расчеты в MATLAB выполняются с двойной точностью, а для представления чисел на экране имеются разные форматы. Нужный формат может быть определен в меню (File/Preferences) либо при помощи команды format. Существуют следующие способы представления чисел (табл.1.1).
Таблица 1.1 Форматы вывода на экран
| Формат | Представление |
| short | Число отображается с 4 цифрами после десятичной точки или в формате short e |
| short e | Число в экспоненциальной форме с мантиссой из 5 цифр и показателем из 3 цифр |
| rat | Представление в виде рационального дробного числа |
| long | Число с 16 десятичными цифрами |
| long e | Число в экспоненциальной форме с мантиссой из 16 цифр и показателем из 3 цифр |
| hex | Число в шестнадцатеричной форме |
Переменные в MATLAB не нужно предварительно описывать, указывая их тип. Все данные хранятся в виде массивов: числовые переменные (внутренний тип numeriс), текстовые строки (char), ячейки (сеll) и структуры (struct). Двумерный массив – это матрица, одномерный – вектор, а скаляр – матрица размера 1x1. Имя переменной должно начинаться с буквы, за ней могут идти буквы, цифры и символ подчеркивания. Допустимы имена любой длины, но MATLAB идентифицирует их по первым 31 символам и различает большие и малые буквы. В MATLAB имеется ряд констант (табл.1.2).
Таблица 1.2 Зарезервированные имена констант
| Имя | Описание |
| ans | Результат последней операции |
| i, j | Мнимая единица |
| pi | Число p |
| eps | Машинная точность |
| realmax | Максимальное вещественное число |
| realmin | Минимальное вещественное число |
| inf | Бесконечность |
| NaN | Нечисловая переменная |
| end | Наибольшее значение индекса размерности массива |
Отметим, что имя NaN (Not-a-Number) зарезервировано для результата операций 0/0, 0*inf, inf-inf и т.п.
Таблица 1.3 Специальные символы
| Символ | Назначение |
| [] | Квадратные скобки используются при задании матриц и векторов |
| Пробел служит для разделения элементов матриц | |
| , | Запятая применяется для разделения элементов матриц и оператора в строке ввода |
| ; | Точка с запятой отделяет строки матриц, а точка с запятой в конце оператора (команды) отменяет вывод результата на экран |
| : | Двоеточие используется для указания диапазона (интервала изменения величины) и в качестве знака групповой операции над элементами матриц |
| () | Круглые скобки применяются для задания порядка выполнения математических операций, а также для указания аргументов функций и индексов матриц |
| . | Точка отделяет дробную часть числа от целой его части, а также применяется в составе комбинированных знаков (.*, .^, ./, .\) |
| … | Три точки и более в конце строки отмечают продолжение выражения на следующей строчке |
| % | Знак процента означает начало комментария |
| ’ | Апостроф указывает на символьные строки, а для включения самого апострофа в символьную строку нужно поставить два апострофа подряд |
В командном окне в режиме диалога проводятся вычисления. Пользователь вводит команды или запускает на выполнение файлы с текстами на языке
MATLAB. Интерпретатор обрабатывает введенное значение и выдает результаты: числовые и строковые данные, предупреждения и сообщения об ошибках. Строка ввода помечена знаком >>.
При работе с MATLAB в командном режиме действует простейший строчный редактор. Обратите особое внимание на применение клавиш Up и Down(стрелки курсора "Вверх" и "Вниз"). Они используются для подстановки после маркера строки ввода >> ранее введенных строк из специального стека, например, для их исправления, дублирования или дополнения. При этом указанные клавиши обеспечивают перелистывание ранее введенных строк снизу вверх или сверху вниз.
Имена переменных должны начинаться с буквы. Знак = соответствует операции присваивания. Нажатие клавиши Enter заставляет систему вычислить выражение и показать результат. Если запись оператора не заканчивается символом «;», то результат выводится в командное окно, в противном случае – не выводится. Если оператор не содержит знака присваивания «=», то значение результата присваивается системной переменной ans (см. рисунок 1.2).
Все значения переменных, вычисленные в течение текущего сеанса работы, сохраняются в специально зарезервированной области памяти компьютера, называемой рабочим пространством системы MATLAB (Workspace).
Для просмотра значения любой переменной из текущего рабочего пространства системы достаточно набрать ее имя и нажать клавишу Enter.
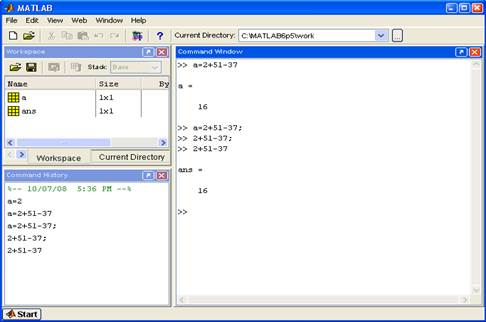
Рисунок 1.2 – Демонстрация выполнения команды присваивания
После окончания сеанса работы с системой MATLAB все ранее вычисленные переменные теряются. Чтобы сохранить в файле на диске компьютера содержимое рабочего пространства системы MATLAB, нужно выполнить команду меню File \Save Workspace As … .По умолчанию расширение имени файла mat, поэтому такие файлы принято называть МАТ-файлами.
Система MATLAB работает как с действительными, так и с комплексными числами. Перед использованием операций с комплексными числами необходимо определить переменную i = sqrt(–1) или j = sqrt(–1). В арифметических выражениях применяются следующие знаки операций:
+, - – сложение, вычитание,
*– умножение,
/ – деление слева направо;
\ – деление справа налево;
^ – возведение в степень.
Система MATLAB позволяет вычислять различные математические функции. Следующие элементарные алгебраические функции имеют в качестве аргумента одно или два действительных (x, y) или одно комплексное (z) число (табл. 1.4).
Таблица 1.4 Элементарные алгебраические функции
| Функция | Описание |
| abs(z), abs(x), | Вычисление модуля комплексного числа z или абсолютного значения действительного числа x. |
| angle(z) | Вычисление аргумента z. |
| sqrt(z),sqrt(x) | Вычисление квадратного корня чисел z и x |
| real(z) | Вычисление действительной части комплексного числа z. |
| imag(z) | Вычисление мнимой части комплексного числа z. |
| round(x) | Округление до целого. |
| fix(x) | Округление до ближайшего целого в сторону нуля. |
| rem(x, y) | Вычисление остатка от деления x на y. |
| exp(z) | Вычисление е в степени x. |
| log(z) | Вычисление натурального логарифма числа x. |
| log10(z) | Вычисление десятичного логарифма числа x. |
Система MATLAB предоставляет возможности для вычисления следующих тригонометрических и обратных тригонометрических функций переменной x (табл.1.5).
Таблица 1.5 Тригонометрических функций
| Функция | Описание |
| sin(x) | Вычисление синуса |
| cos(x) | Вычисление косинуса |
| tan(x) | Вычисление тангенса |
| asin(x) | Вычисление арксинуса |
| acos(x) | Вычисление арккосинуса |
| atan(x) | Вычисление арктангенса |
| atan2(y, x) | Вычисление арктангенса по координатам точки |
Порядок выполнения
1. В командном окне задать значения переменных, согласно варианту задания, представленному в таблице 1.6.
2. Записать выражение на языке MATLAB.
Таблица 1.6 Варианты заданий
| № | Выражение | Переменные |
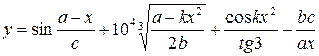 | 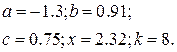 | |
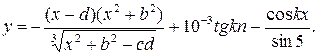 | 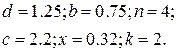 | |
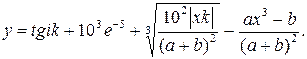 | 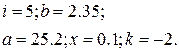 | |
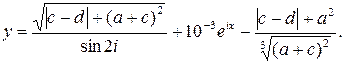 | 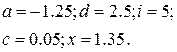 | |
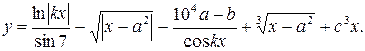 | 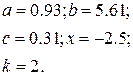 | |
 | 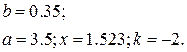 | |
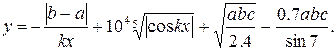 | 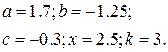 | |
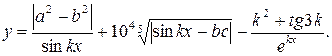 | 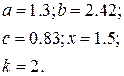 | |
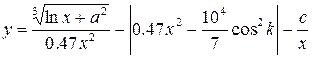 | 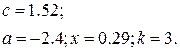 | |
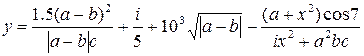 | 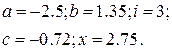 | |
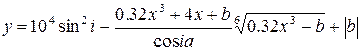 | 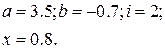 | |
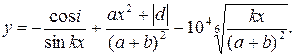 | 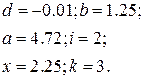 | |
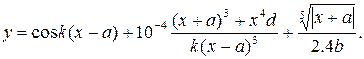 | 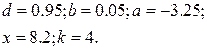 | |
| Продолжение таблицы 1.6 | ||
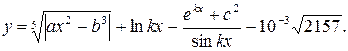 | 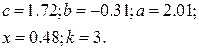 | |
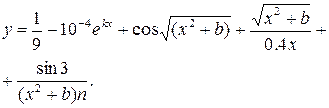 | 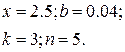 |
Содержание отчета
1. Цель работы.
2. Пример расчета и вывода данных.
Контрольные вопросы
1. Для чего служит команда HELP?
2. Перечислите основные команды MATLAB для работы в режиме прямых вычислений.
3. С помощью какой команды устанавливается формат чисел?
4. Перечислите основные системные переменные MATLAB.
5. Приведите примеры математических функций системы MATLAB.
Практическое занятие № 2
