Методические указания к решению задачи. Расчет балки на изгиб следует условно разделить на три этапа:

Расчет балки на изгиб следует условно разделить на три этапа:

v Определение опорных реакций

На этом этапе осуществляется решение задачи на равновесие твердого тела в соответствии с методологией теоретической механики из раздела «Статика. Плоская произвольная система сил».

Для того чтобы балка могла сопротивляться действию внешней нагрузки, она должна быть соответствующим образом закреплена.

Обычно используются три вида опорных закреплений, которым соответствует определенное количество накладываемых связей (см. таблицу 5.1).

Таблица 5.1 – Виды опор и их реакции

Вид опоры	Схема и реакции	Характеристика опоры
Шарнирно - подвижная		Опора препятствует перемещению балки по вертикали; разрешает горизонтальное смещение и поворот сечения.
Шарнирно - неподвижная		Опора препятствует линейному перемещению балки в любом направлении, разрешает поворот сечения.
Жесткое защемление (жесткая заделка)		Невозможны линейное перемещение сечения и поворот.

Для определения реакций опор необходимо:

Освободить балку от связей (опор) и изобразить действующие на неё заданные нагрузки. В данную расчетную схему включить неизвестные опорные реакции, векторы которых должны быть направлены перпендикулярно оси балки. Для неподвижной опоры следует дополнительно ввести опорную реакцию, вектор которой направлен вдоль оси балки. Направления векторов всех неизвестных опорных реакций на данном этапе расчета можно назначать произвольным образом.

Распределенную нагрузку необходимо заменить эквивалентной ей сосредоточенной силой, действующей в том же направлении и приложенной в центре тяжести эпюры распределенной нагрузки (рисунок 5.1).

Рисунок 5.1

Выбрать систему координат и составить уравнения равновесия. Начало координат удобнее совмещать с левым концом балки, за ось X принять ось балки. Представляется целесообразным составлять уравнения равновесия моментов относительно тех точек балки, в которых приложены неизвестные опорные реакции. При наличии внешней нагрузки, вызывающей горизонтальную составляющую у реакции в неподвижной опоре, необходимо добавить уравнение равновесия проекций действующих нагрузок, включая неизвестные опорные реакции, на горизонтальную ось балки.

Решить составленные уравнения равновесия. В случае отрицательных значений у вычисленных опорных реакций следует изменить направления соответствующих векторов на противоположные.

Проверить правильность полученных результатов по уравнению, которое не было использовано в ходе решения, путем подстановки в него вычисленных опорных реакций с учетом их уточненных направлений.

v Определение поперечных сил и изгибающих моментов по длине балки

Решение этой задачи следует проводить в следующей последовательности:

1. Балку разделить на расчетные участки, границы которых совпадают с точками приложения сосредоточенных сил, сосредоточенных моментов или с точками начала и конца действия распределенной нагрузки;

2. Применяя метод сечений для данной задачи, последовательно переходя от одного участка к другому, условно разрезать балку в произвольном сечении на каждом участке;

3. Для каждого участка составить условия статического равновесия отсеченной части балки (левой или правой), из которых получить выражения для определения поперечной силы Q и изгибающего момента M (через текущую координату X) для данного участка;

4. Подставляя в найденные уравнения значения абсцисс на каждом участке вычислить в ряде сечений величины поперечных сил и изгибающих моментов.

Если в пределах участка поперечная сила меняет знак, необходимо найти величину текущей координаты x, которой соответствует нулевое значение поперечной силы Q=0. На эпюре изгибающего момента этой координате будет соответствовать экстремальное значение М_экс, которое следует вычислить;

- при записи выражений для Q и M следует придерживаться определенных правил:

• поперечная сила численно равна алгебраической сумме внешних сил, действующих по одну сторону от рассматриваемого сечения. Внешняя сила дает положительное слагаемое, если стремится повернуть оставшуюся часть балки относительно данного сечения по часовой стрелке. Следует мысленно установить шарнир в рассматриваемом сечении, относительно которого поворачивается отсеченная часть балки от действующих сил;

• изгибающий момент численно равен сумме моментов относительно рассматриваемого сечения от всех нагрузок, действующих по одну сторону от этого сечения. Момент от нагрузки считается положительным, если вызывает сжатие верхних волокон рассматриваемой части балки. Мысленно установить в этом сечении заделку и рассмотреть состояние верхних волокон отсеченной части балки в зависимости от данного вида нагрузки.

Графически правило знаков для поперечных сил Q и изгибающих моментов M в зависимости от движения к сечению показано на рисунке 5.2.

Рисунок 5.2

- по вычисленным значениям поперечных сил и изгибающих моментов построить в масштабе соответствующие эпюры. Положительные значения откладывать от нулевой линии вверх, отрицательные – вниз. Полученные плоские фигуры заштриховать вертикальными линиями с указанием знаков.

v Подбор сечения балки (проектный расчет) выполняется по методу допускаемых напряжений.

Особенностью расчета изгиба консольных балок является отсутствие необходимости определения опорных реакций. В этом случае определение поперечных сил Q и изгибающих моментов M целесообразно начинать от свободного торцевого сечения.

Пример решения задачи

Дано: стальная балка на двух опорах, нагруженная системой внешних сил, лежащих в силовой плоскости, изображенной на рисунке 5.3, а. При расчетах принято: F= 20кН, m= 40кН∙м, q=100кН/м, [σ] = 160 МПа.

Требуетсярешить следующие задачи:

1. Определить опорные реакции балки;

2. Построить эпюры поперечных сил Q и изгибающих моментов М;

3. Из расчета на прочность подобрать сечение в форме стандартного профиля двутавровой прокатной балки.

Решение:

Определение опорных реакций (рисунок 5.3, б)

Представим балку как свободное тело, для чего отбросим опоры А и D, а их действие на балку заменим реакциями X_A, Y_A и Y_D.

Заменяем распределенную нагрузку .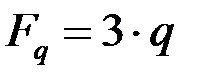

При составлении уравнений равновесия примем для удобства правило знаков, по которому момент силы или момент пары сил, стремящийся повернуть балку вокруг моментной (неподвижной) точки в направлении вращения часовой стрелки, положительный.

Составим уравнения равновесия:

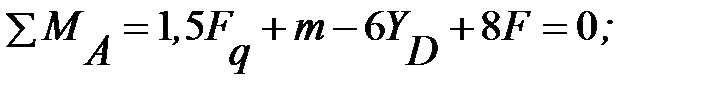
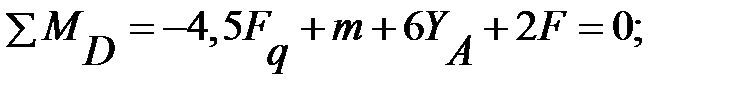
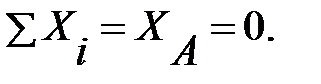
Откуда, получаем Y_D =108кН; Y_A≈212 кН; X_A=0.

Проверка. Правильность нахождения реакций опор можно оценить, например, составив уравнение суммы проекций всех сил на ось Y:

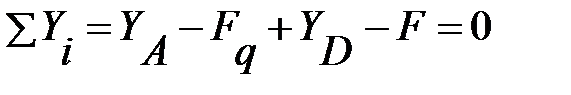или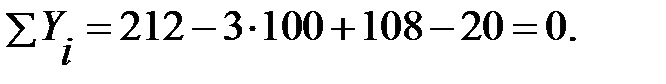

Следовательно, опорные реакции определены верно.

Построение эпюр поперечных сил Q и изгибающих моментов М для участков балки (рисунок 5.3, б).

1) Разбиваем балку на участки.

За границы участков принимаем сечения, где приложены момент М или сила F, а также границы действия распределенной нагрузки q. Направление обхода участков выбираются в зависимости от удобства вычислений, чем меньше нагрузок, тем проще формулы для вычислений. В данном случае имеем четыре участка (очередность буквенного обозначения определяет направление обхода, например, LD – начало обхода от точки L к D):

I – AB: 0≤ x1≤ 3м, (x1A=0; x1B=3м);

II – BC: 0≤ x2≤ 1м, (x2B=0; x2C=1м);

III – LD: 0≤ x3≤ 2м, (x3L=0; x3D=2м);

IV – DC: 0≤ x4≤ 2м, (x4D=0; x4C=2м).

Участок I. Выбираем начало координат в точке (опоре) А и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии х1 от начала координат. Мысленно отбрасываем правую часть балки и рассматриваем равновесие оставшейся левой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого се­чения:

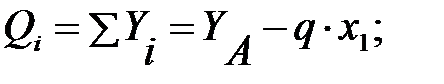
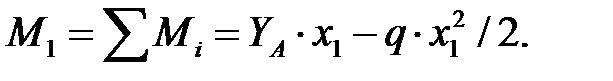
Задавая значения x₁, соответствующие границам участка I, по­лучим

Q_1A(x1=0) =Y_A=212кН; Q_1B(x1=3м) =Y_A-3q=-88кН;

M_1A(x1=0) =0кН∙м; M_1B (x1=3м) =3Y_A-32q/2=186 кН∙м.

Т.к. сила Q в пределах участка меняет знак, то, очевидно, имеется значение Q=0. Согласно дифференциальной зависимости 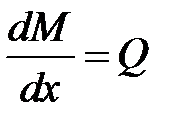, очевидно, что в точке пересечения (Q=0) изгибающий момент принимает экстремальное значение. Для нахождения этого экстремума вычисляем его координату по формуле: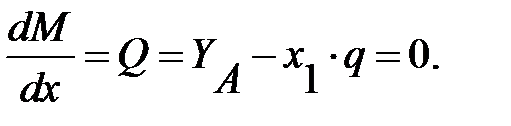

Откуда, x₁^Э=Y_A/q= 212/100=2,12 м.

Подставив значение x₁^Э= 2,12 м в уравнение момента для участка, найдем величину экстремального момента

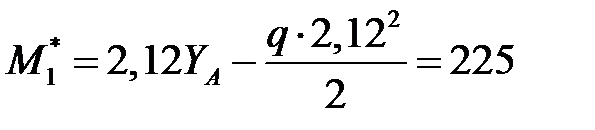кН·м.

Участок II. Выбираем начало координат в точке В и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии х₂ от начала координат. Мысленно отбрасываем правую часть балки и рассматриваем равновесие оставшейся левой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

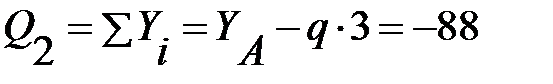кН (не зависит от х₂);

.

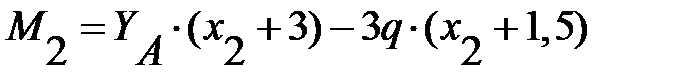Задавая значения x₂, соответствующие границам участка II, по­лучим значения изгибающего момента

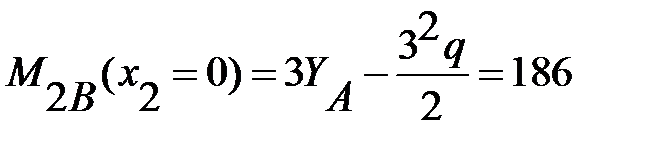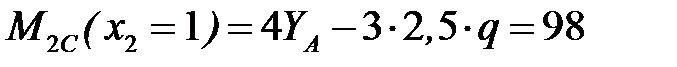кН·м;

кН·м.

Участок III. Выбираем начало координат в точке L и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии x₃ от начала координат. Мысленно отбрасываем левую часть балки и рассматриваем равновесие оставшейся правой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

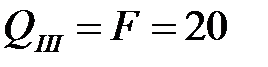кН (не зависит от х₃);

.

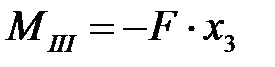Задавая значения x₃, соответствующие границам участка III, по­лучим значения изгибающего момента

;

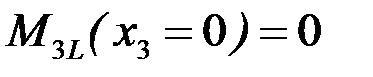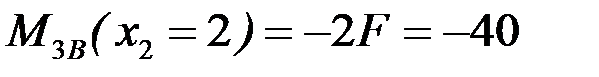кН·м.

Участок IV. Выбираем начало координат в точке D и приступаем к построению эпюр поперечных сил Q и изгибающих моментов М, применяя метод сечений.

Проводим сечение в пределах участка на расстоянии x₄ от начала координат. Мысленно отбрасываем левую часть балки и рассматриваем равновесие оставшейся правой части. Составляем уравнения — сумму проекций всех сил на вертикальную ось и сумму моментов всех сил относительно рассматриваемого сечения:

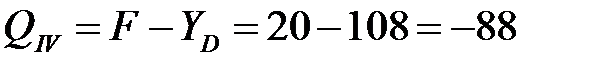кН (не зависит от х₄);

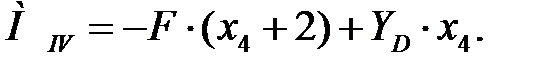
Задавая значения x₄, соответствующие границам участка IV, получим значения изгибающего момента

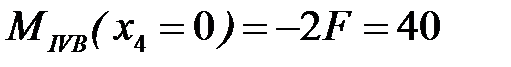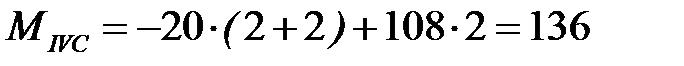кН·м.

кН·м.

По результатам проведенных расчетов строятся эпюры поперечных сил Q и изгибающих моментов M. Эти эпюры представлены на рисунках 5.3 в - г.

Определение сечения балки по условию прочности

Определим из расчета на прочность размеры поперечного сечения балки в форме двутавра.

Подбор сечения производится по максимальному изгибающему моменту M_max. Опасным является сечение в точке экстремума, где действует максимальный по абсолютному значению изгибающий момент M_max =225 кН·м.

Минимально допустимый момент сопротивления сечения изгибу равен

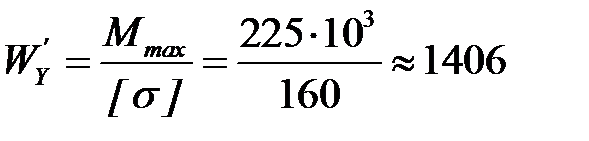см³.

Стандартный профиль двутавра выбирается по ГОСТ 8239-89 (приложение С.5). Из таблицы сортамента выбираем двутавр № 50:

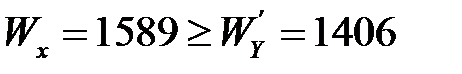см³, площадь - A=100см².

Рисунок 5.3

Вопросы и задания для самоконтроля

1. Какие внутренние силовые факторы возникают в поперечных сечениях балки при изгибе? Какое принято правило знаков при их определении?

2. Какие применяются основные правила проверки эпюр Q и M?

3. Как определяются нормальные напряжения в произвольной точке сечения и максимальные напряжения? Какой вид имеет эпюра нормальных напряжений в сечении?

4. Что такое осевой момент инерции сечения и момент сопротивления сечения при изгибе? Как они определяются для прямоугольного, круглого и кольцевого сечений?

5. Каким образом определяют опасное сечение балки?

6. Как записывается условие прочности балки при изгибе? Какие задачи решаются на основе условия прочности?

7. Что понимается под рациональной формой сечения балки при изгибе? В чём преимущества применения балок стандартного профиля?

Варианты тестовых заданий

№	Задание	Ответы
5.1	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.2	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.3	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.4	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.5	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.6	Для заданной схемы нагружения балки укажите правильную эпюру изгибающих моментов.
5.7	Для заданной схемы нагружения балки укажите правильную эпюру поперечных сил.
5.8	Определить для заданной схемы нагружения изгибающий момент в опасном сечении балки длиной l.	M-q∙l2 M+q∙l2 M+q∙l2/6 M-q∙l2/2
5.9	Расположите номера точек в порядке возрастания нормальных напряжений при изгибе.	1. 4, 1, 2, 3 2. 2, 1, 3, 4 3. 2, 3, 4, 1 4. 4, 2, 3, 1

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ А

Оформление титульного листа контрольной работы

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ СЕРВИСА

Кафедра Инженерных дисциплин