Задачи, описывающие движение

Основные компоненты задач, описывающих движение:

S – пройденный путь (пройденное расстояние);

V – скорость движущегося тела;

t – время движения.

Допущения, которые обычно принимаются в условиях этих задач:

1) движение на отдельных участках считается равномерным (если не указано противное), т. е.

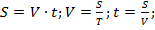
2) величины должны быть выражены в одной системе единиц;

3) повороты движущихся тел считаются мгновенными;

4) если тело движется по течению реки, то его скорость равна сумме скорости тела в стоячей воде и скорости течения:

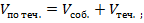
если тело движется против течения, то

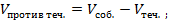
5) если два тела начинают движение одновременно навстречу друг другу, V₁ и V₂ – скорости тел; S – первоначальное расстояние между телами, то время в пути до встречи у обоих тел одинаково:

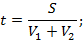
6) если два тела начинают движение одновременно в одном направлении, 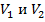– скорости тел, V₁ > V₂, S – первоначальное расстояние между телами, то время, в течение которого одно тело догонит другое (время в пути до встречи)

;

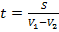7) если в задаче отсутствуют единицы длины, то весь пройденный путь можно принять за единицу;

8) если движение двух точек со скоростями V₁ и V₂ (V₁ > V₂) происходит по окружности длины l, то при движении в противоположных направлениях точки будут встречаться через время 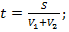а при движении в одном направлении (при условии одновременного старта из одного положения) точка с большей скоростью нагонит другую, обогнав ее на целый круг:

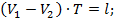Т – время в пути до встречи.

При решении задач полезно (но не обязательно) сделать чертеж. Неизвестные величины можно обозначать X, Y, Z или оставить обозначения, принятые в физике.

Задача 1. Расстояние между городами А и В равно 60 км. Два поезда выходят одновременно: один из А в В, другой из В в А. Поезд, идущий из А в В, пройдя 20 км, стоит полчаса, затем отправляется дальше и через 4 мин встречает поезд, идущий из В в А. Оба поезда прибывают к месту назначения одновременно. Определить скорости поездов.

Решение.Нарисуем для удобства схему движения поездов (рис. 1.1), отметив на отрезке АВ места встречи и стоянок поездов, а также направления движений. Такой рисунок делать не обязательно, поскольку при решении задач на движение можно составлять таблицы с первоначальными данными или изображать график движения в системе координат .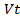

Рис. 1.1 Схема движения поездов.

AВ = 60 км; АС = 20 км; СД – путь, пройденный первым поездом за 4 мин; Д – место встречи поездов.

V₁ (км/ч) – скорость поезда, идущего из А в В (первого поезда);

V₂ (км/ч) – скорость поезда, идущего из В в А (второго поезда).

Первый поезд стоял полчаса, поэтому затратил на путь от А до В время 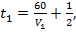, второй поезд затратил на путь от В до А время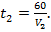

Оба поезда прибыли к месту назначения одновременно, т. е. t₁ = t₂, или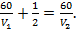

К моменту встречи в точке Д первый поезд прошел расстояние АД = АС + СД, где АС = 20 км, а СД – путь, пройденный первым поездом за 4 мин. Поскольку расстояние дано в километрах, а скорость в километрах в час, то минуты надо перевести в часы: 4 мин составляют 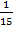часа.

Тогда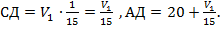

Расстояние АД первый поезд прошел за время

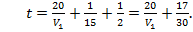
За это же время второй поезд прошел расстояние

;

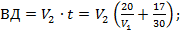
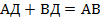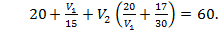
Полученные уравнения образуют систему:

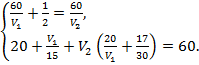
Выразим из первого уравнения V₁через V₂ и подставим полученное значение во второе уравнение системы:

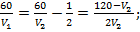
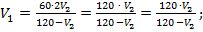
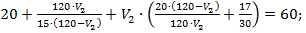
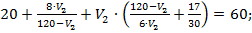
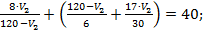
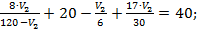
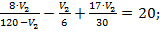
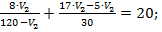
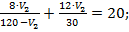
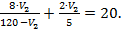
Приведем выражение к общему знаменателю:

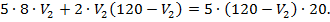
Разделим левую и правую части уравнения на 2:

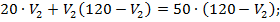
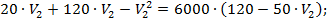
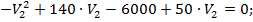
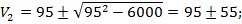
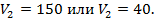
Рассмотрим оба варианта.

Если 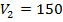км/ч, тогда 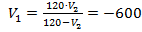км/ч. По условию задачи скорости являются положительными величинами, поэтому 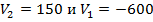– посторонние корни, не удовлетворяющие условиям. Если 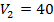км/ч, то 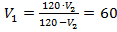км/ч. Полученные значения удовлетворяют условиям задачи.

Ответ: скорости поездов равны 60 и 40 км/ч.

Задача 2. Два автомобиля выехали одновременно из пунктов А и В навстречу друг другу. Через 16 ч после встречи автомобиль, следовавший из А, прибыл в В, а через 25 ч после встречи автомобиль, выехавший из В, прибыл в А. Сколько часов каждый автомобиль был в пути?

Решение. Нарисуем схему движения автомобилей

(рис. 1.2).

Рис. 1.2 Схема движения автомобилей.

V₁, V₂ – скорости автомобилей; расстояние АВ = S; С – место встречи ав­­то­мобилей; t₁, t₂ – время в пути на АВ соответственно первого и второго автомобилей. Поскольку автомобили выехали одновременно, то в пути до встречи они были одно и то же время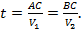

После встречи первый автомобиль проехал расстояние ВС за 16 ч, т. е. 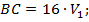расстояние АС второй автомобиль преодолел за 25 ч, т. е.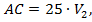

тогда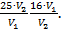

Первый автомобиль прибыл в пункт В через 16 ч после встречи, а второй – через 25 ч, т. е. второй автомобиль был в пути дольше первого на 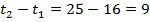ч.

Запишем систему уравнений:

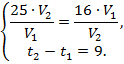
Поскольку 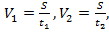то система принимает вид

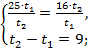
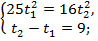
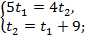
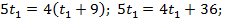
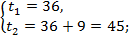
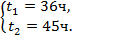
Ответ: время в пути первого автомобиля составляет 36 ч, а второго – 45 ч.

Замечание. В этой задаче можно было принять расстояние АВ за единицу: S = 1, тогда в системе вместо уравнения 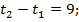можно было записать уравнение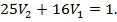

Задача 3. Студенты взяли на лодочной станции напрокат лодку. Сначала они спустились на 20 км вниз по течению реки, затем повернули обратно и вернулись на лодочную станцию, затратив на всю прогулку 7 ч. На обратном пути, на расстоянии 12 км от лодочной станции, они встретили плот, проплывавший мимо лодочной станции как раз в тот момент, когда они отправились на прогулку. Определить, с какой скоростью двигалась лодка вниз по течению реки и какова скорость течения.

Решение. Нарисуем схему движения лодки (рис. 1.3).

Рис. 1.3.Схема движения лодки

.

АВ = 20 км – расстояние, пройденное вниз по реке; у (км/ч) – скорость течения реки; х (км/ч) – скорость лодки в стоячей воде; С – место встречи лодки и плота; АС = 12 км.

По условию задачи на путь от А до В и обратно студенты затратили 7 ч, (х + у) – скорость лодки при движении по течению реки, (x – y) – скорость лодки при движении против течения, поэтому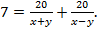

За то время, что плот прошел расстояние АС = 12 км, студенты преодолели расстояние АВ = 20 км и ВС = (20 – 12) = 8 км, т. е.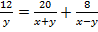

Запишем полученные уравнения в систему и решим ее.

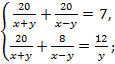
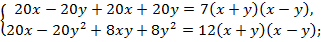
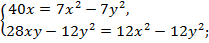
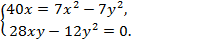
По условию задачи x > 0, y > 0, поэтому из второго уравнения системы: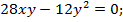

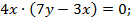
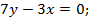
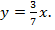
Подставив у в первое уравнение системы, получим

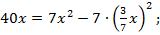
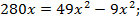
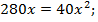х = 7, тогда у = 3.

Скорость лодки при движении вниз по течению реки равна (х + у), т. е. 10 км/ч, а скорость течения реки 3 км/ч.

Ответ: скорость лодки по течению реки 10 км/ч, а скорость течения реки 3 км/ч.

Задача 4. Два автомобиля, двигаясь по кольцевой дороге с постоянными скоростями в одном направлении, оказываются рядом через каждые 56 мин. При движении с теми же скоростями в противоположных направлениях автомобили встречаются через каждые 8 мин. За какое время проезжает всю кольцевую трассу каждый автомобиль?

Решение.Сразу следует заметить, что в отличие от реальной жизни в задаче предполагается, что автомобили двигаются по одной и той же трассе, а не по концентрическим окружностям.

Поскольку длина кольцевой дороги не указана в условиях задачи, то можно предположить, что ее длина составляет S метров или принять длину окружности за новую единицу длины. Пусть V₁ (м/мин) и V₂ (м/мин) – скорости автомобилей, V₁ > V₂. Время, которое требуется каждому автомобилю для проезда по всей кольцевой трассе, составляет t₁ и t₂ минут, причем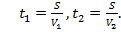

Из условия задачи известно, что 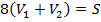и 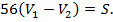Эти два уравнения запишем в систему, выразив скорости через время, что позволит оставить в уравнениях только два неизвестных:

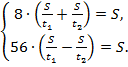
Сократим на S и получим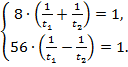

Точно такую же систему можно было записать, если сразу предположить, что S = 1.

Перепишем систему в виде 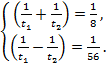и сначала почленно сложим, а затем почленно вычтем, левые и правые части уравнений, тогда получим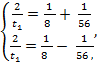

откуда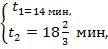

Ответ: один из автомобилей проезжает всю кольцевую дорогу за 14 мин, а другой – за 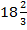мин.